余割的导数 - Mathority

在本文中，我们将解释如何导出函数（公式）的余割。您还可以找到逐步解决余割导数的练习。最后，您将能够看到此类三角导数的公式演示。

余割导数公式

x 的余割导数等于减去 x 的余弦除以 x 的平方正弦所得的商。

$f(x)=\text{cosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}$

使用三角公式，我们还可以将 x 的余割的导数定义为减去 x 的余切乘以 x 的余割的乘积。

$f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}=-\cfrac{\text{cos}(x)}{\text{sen}(x)}\cdot \cfrac{1}{\text{sen}(x)}=-\text{cot}(x)\cdot \text{cosec}(x)$

如果我们应用链式法则，函数余割的导数减去函数导数乘以函数余弦的乘积，再除以函数的正弦平方。

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

因此，用于导出函数余割的公式如下：

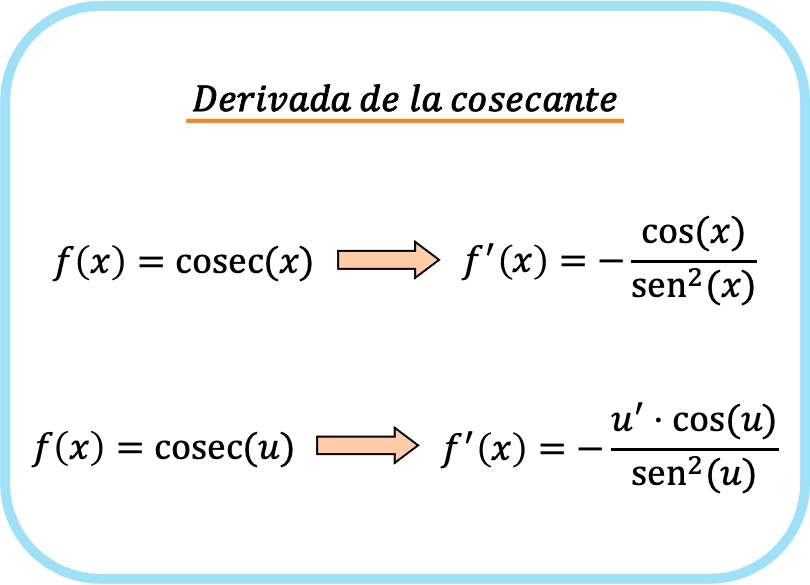
余割导数的例子

了解了余割导数的公式是什么之后，我们现在将给出几个例子。这样您就可以准确地看到函数的余割是如何导出的。

示例 1：2x 余割的导数

在这个例子中，我们将看到 2x 余割的导数是多少：

$f(x)=\text{cosec}(2x)$

余割自变量函数与x不同，因此我们需要将余割导数法则与链式法则结合使用。

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

所以，要求这个三角函数的导数，只需代入前面公式中的值即可：在余弦和正弦参数中我们放入 2x，u’ 对应于 2x 的导数，即 2：

$f(x)=\text{cosec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2\cdot \text{cos}(2x)}{\text{sen}^2(2x)}$

示例 2：x 平方余割的导数

在本练习中，我们将了解 x 平方余割的导数是多少：

$f(x)=\text{cosec}(x^2)$

从逻辑上讲，该三角函数的导数可以使用余割导数公式求解：

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

x 平方的导数为 2x，因此 x 的余割对 2 次方的导数为：

$f(x)=\text{cosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x\cdot \text{cos}(x^2)}{\text{sen}^2(x^2)}$

示例 3：指数函数的三次余割的导数

$f(x)=\text{cosec}^3(e^{5x})$

无论函数的参数是什么，函数余割的导数规则是：

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

但在这种情况下，我们有一个复合函数，因为余割被提高到三，而且，在它的参数中有一个指数函数。因此，为了对整个函数求导，我们需要多次应用链式法则：

$\begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}$

解决了余割导数的问题

推导以下余割函数：

$\text{A) }f(x)=\text{cosec}(x^4-2x^2)$

$\text{B) }f(x)=\text{cosec}(x^3+e^x-10)$

$\text{C) }f(x)=\text{cosec}\bigl(\ln(x^3+7x^2)\bigr)$

$\text{D) }f(x)=\text{cosec}\bigl(\text{arccos}(x^7)\bigr)$

$\text{E) }f(x)=\text{cosec}\left(\sqrt{9x^2-4x}\right)$

查看解决方案

$\text{A) }f('x)=-\cfrac{(4x^3-4x)\cdot \text{cos}(x^4-2x^2)}{\text{sen}^2(x^4-2x^2)}$

$\text{B) }f('x)=-\cfrac{(3x^2+e^x)\cdot \text{cos}(x^3+e^x-10)}{\text{sen}^2(x^3+e^x-10)}$

$\begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}$

$\begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}$