在此页面上,您将找到有关抛物线的所有内容:它是什么、它代表什么、它的元素(焦点、准线、顶点等)、它的方程(具有不同类型的抛物线方程)、示例、已解决的练习、它的特性、它的应用、……
什么是比喻?
抛物线是一个含义截然不同的概念,但其数学定义如下:
在数学中,抛物线是平面上与固定点(称为焦点)和固定线(称为准线)等距的点的轨迹。
因此,抛物线中的任何点到其焦点和准线的距离都相同。

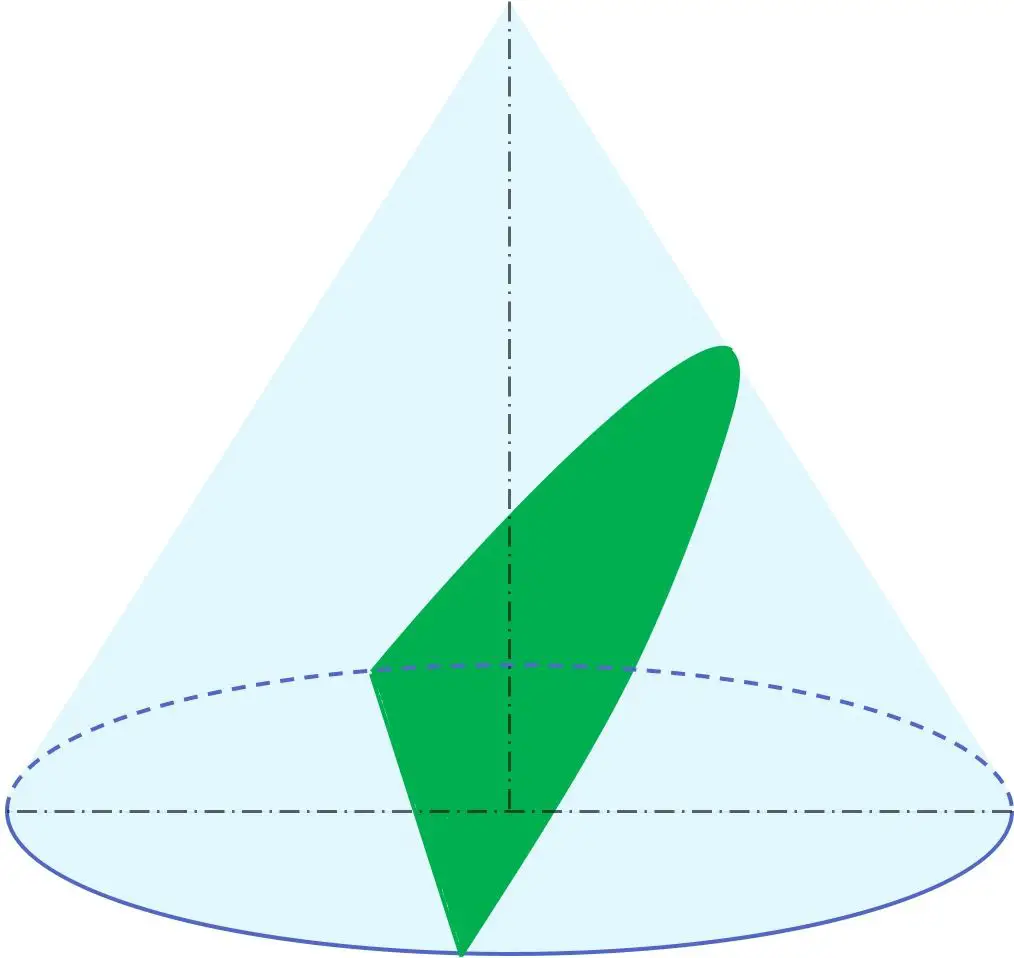
此外,在几何学中,抛物线与圆周、椭圆和双曲线一样是圆锥曲线之一。换句话说,可以从圆锥得到抛物线。
特别地,抛物线由圆锥体与相对于旋转轴的倾斜角等于圆锥体母线角的平面的截面产生。因此,包含抛物线的平面平行于圆锥体的母线。
抛物线的要素
抛物线的特征取决于以下元素:
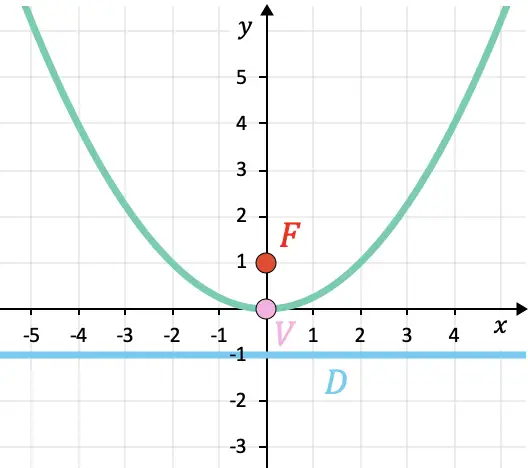
- 焦点(F) :是抛物线内的固定点。抛物线任意点到焦点的距离等于该点到抛物线准线的距离。
- 准线(D) :它是抛物线外部的一条固定线。抛物线的一点到准线的距离与到抛物线焦点的距离相同。
- 参数(p) :是焦点到导演的距离。
- 半径矢量(R) :是将抛物线的一点连接到焦点的线段。其值与该点到准线的距离一致。
- 轴(E) :是垂直于通过焦点的准线的线,是抛物线的对称轴,在下图中它对应于计算机轴(Y轴)。也称为焦轴。
- 顶点(V) :是抛物线与其轴的交点。
- 焦距:焦点与顶点之间的距离,或准线与顶点之间的距离。它的值总是等于
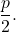
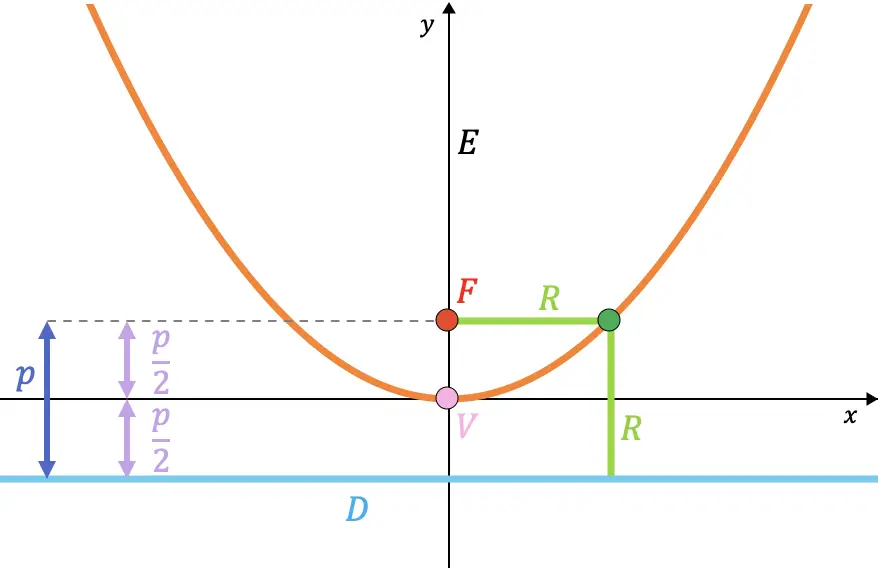
右边
抛物线的右侧是抛物线内部穿过焦点且与准线平行的弦。
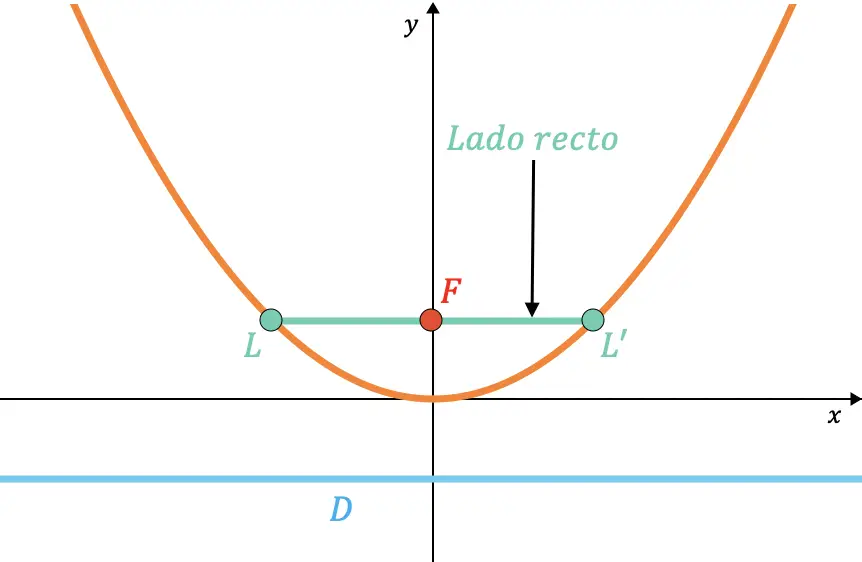
类似地,可以证明右侧的长度始终是参数值的两倍
![]()
![]()
另一方面,穿过右侧两端的与抛物线相切的两条线与右侧本身形成 45° 角,并且也在抛物线的顶部相交。
抛物线方程
抛物线方程是二次函数的一种,因为它必须始终具有至少 1 个平方项。此外,抛物线方程取决于其水平或垂直方向。
因此,在解析几何中,有几种方法可以在数学上表达抛物线:正则方程或简化方程、普通方程和抛物线的一般方程。
抛物线的简化方程或正则方程
简化方程或正则方程与其他抛物线方程的区别在于,抛物线的顶点是坐标 的原点,即点 (0,0)。
抛物线简化方程的形式取决于它是水平的还是垂直的。请看下面的图形表示,其中指出了 4 种可能的变体:
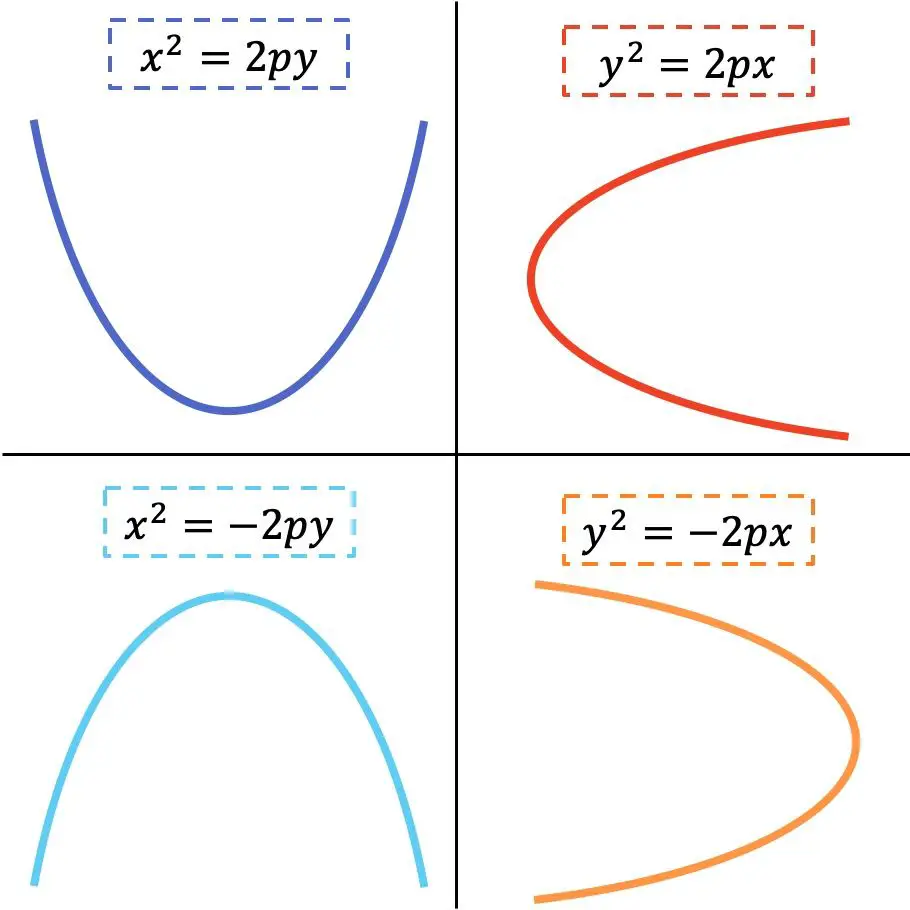
金子
![]()
是抛物线的特征参数。
正如您在上图中看到的,当变量x平方时,抛物线是垂直的,另一方面,当变量y平方时,抛物线是水平的。另一方面,抛物线分支的方向取决于方程的符号。
普通抛物线方程
我们刚刚看到了当抛物线的顶点或中心对应于坐标原点时(简化或规范方程),抛物线的方程是什么样子,但是如果顶点位于“原点”之外,抛物线的方程是什么?
当抛物线的顶点为任意点时,我们使用抛物线的常方程,其表达式为:
![]()
其中抛物线的中心或顶点是点
![]()
前面的方程对应于垂直方向的抛物线,即抛物线的焦轴平行于Y轴。
同样,要定义水平方向的抛物线(其焦轴平行于 X 轴),我们必须使用抛物线普通方程的以下变体:
![]()
与之前一样,抛物线的中心或顶点是点
![]()
抛物线的一般方程
到目前为止,我们分析的所有抛物线方程都是用来表达水平或垂直抛物线。但显然抛物线也可以是斜线或斜线。
那么,为了表达这种类型的抛物线,我们使用一般抛物线方程,其公式如下:
![]()
上式是抛物线当且仅当系数
![]()
和
![]()
不同时为零,并且满足以下条件:
![]()
如何从方程中找到抛物线的顶点、焦点和准线的示例
在许多抛物线练习和问题中,要求您计算某个抛物线的顶点、焦点和准线。因此,让我们通过一个例子来看看这是如何完成的:
- 求下列抛物线的顶点、焦点和准线:
![]()
解决这类抛物线问题的根本是确定抛物线的参数p 。在这种情况下,抛物线方程对应于简化方程或规范方程(垂直抛物线):
![]()
因此,参数p为:
![]()
![]()
![]()
另一方面,由于抛物线遵循简化方程或正则方程,这意味着它的顶点或中心位于坐标原点:
![]()
一旦我们知道了抛物线的顶点和参数值,我们就可以很容易地找到它的焦点和准线。
方程的二次项是变量x ,因此抛物线的轴将平行于 OY 轴,事实上,由于其顶点是点 (0,0),因此抛物线的轴将是 OY轴本身。那么,抛物线的焦点始终位于抛物线的轴上,距离为
![]()
从抛物线的顶部开始,所以它的坐标是:
![]()
![]()
![]()
同样,指导线将是距离
![]()
从抛物线的顶点开始,这是坐标原点。因此,该直线的方程为:
![]()
![]()
![]()
抛物线已绘制在下面,您可以检查结果:
抛物线的性质
所有抛物线都具有以下性质:
- 抛物线是一条开放曲线,换句话说,它是由两条没有共同点的分支无限延伸而成。
- 每个抛物线具有唯一的对称轴,所述抛物线的顶点位于该对称轴。
- 垂直方向的抛物线当其分支向上时是凸的;相反,如果其分支向下,则抛物线是凹的。
- 抛物线的偏心率等于单位 (1)。偏心率是一个系数,在这种情况下,其计算方法是用从焦点到抛物线中心的距离除以从顶点到准线的距离(并且这两个距离的值始终一致)。
- 从前面的性质可以看出,所有抛物线都是相似或相似的。
- 抛物线没有渐近线。
抛物线应用
既然您已经非常熟悉比喻的含义,您可能会想……比喻的意义是什么?
好吧,即使你看起来不像,抛物线的几何形状在现实生活中也很常见。例如,很多时候,当投掷球时,它会做抛物线运动,尤其是在篮球比赛中。抛物线方程对于分析研究球所遵循的抛物线路径非常有用。
该碟形天线的另一个应用涉及天线(因此称为抛物面天线)。由于落在平行于对称轴的抛物面形状物体上的每条射线都会直接反射向焦点,也就是说,到达抛物面天线的所有射线都集中在焦点处,这可以以不同的方式使用。这就是为什么比喻的焦点如此重要。
修复了菜品问题
练习1
计算抛物线的顶点、焦点和准线,其方程如下:
![]()
首先,抛物线将是水平的,因为它遵循以下抛物线简化或规范方程的表达式:
![]()
所以它的参数p为:
![]()
![]()
![]()
另一方面,由于抛物线遵循简化方程或正则方程,这意味着它的顶点或中心位于坐标原点:
![]()
一旦我们知道了抛物线的顶点和参数值,我们就可以轻松计算出它的焦点和准线。
方程的二次项是变量,也就是说,抛物线的轴将平行于 OX 轴,事实上,由于其顶点是点 (0,0),l 抛物线的轴将是OX 轴本身。那么,抛物线的焦点始终位于抛物线的轴上,距离为
![]()
从抛物线的顶部开始,其坐标为:
![]()
![]()
![]()
同样,引导线也位于一定距离处
![]()
从抛物线的顶点开始,抛物线的顶点是坐标原点并且垂直于其焦轴。因此,该直线的方程为:
![]()
![]()
![]()
练习2
求抛物线的顶点、焦点和准线,其方程如下:
![]()
抛物线根据其常方程(轴平行于Y轴)定义,其公式为:
![]()
所以它的参数p为:
![]()
![]()
![]()
另一方面,在这种情况下,抛物线的普通方程意味着它的中心不在坐标原点,另一方面,抛物线顶点的笛卡尔坐标是括号中的数字,其符号发生了变化:
![]()
一旦我们知道了抛物线的顶点和参数值,我们就可以计算出它的焦点和准线。
方程的二次项是变量x ,使得抛物线的轴平行于 OY 轴。因此,抛物线的焦点始终位于抛物线的轴上,距离为
![]()
从抛物线的顶点开始,这样焦点坐标就是顶点的坐标,添加
![]()
垂直:
![]()
![]()
![]()
![]()
同样,准线将是位于一定距离处的水平线
![]()
从抛物线的顶部。因此,该直线的方程为:
![]()
![]()
![]()
![]()
练习3
求一个与横坐标轴平行、以点V(5,2)为顶点、焦点为点P(8,2)的抛物线方程。
在这种情况下,抛物线的顶点并不是坐标原点,因此我们需要用普通方程来定义该陈述的抛物线。此外,抛物线的焦轴平行于 x 轴,这意味着抛物线将水平定向(分支将向右或向左),因此方程的二次项必须是变量y :
![]()
那么我们可以将抛物线顶点的坐标代入方程:
![]()
我们现在需要找到参数的值
![]()
炉膛到炉顶的距离必须是
![]()
因此我们可以找到参数的值
![]()
根据以下等式:
![Rendered by QuickLaTeX.com \left. \begin{array}{c} V(5,2) \\[2ex] P(8,2) \end{array} \right\} \longrightarrow \ 8-5 = \cfrac{p}{2}](https://mathority.org/wp-content/ql-cache/quicklatex.com-91d82e4dce56ca1c48f7c2dba2be5561_l3.png)
![]()
![]()
![]()
![]()
最终,抛物线方程为:
![]()
![]()
![]()