Magic Squares是一款数学益智游戏,以有趣且令人兴奋的方式训练我们的计算技能。这就是为什么它是向年轻学生教授数学的最佳资源之一。
什么是魔法阵,如何解析?
幻方是一种由不同盒子组成的表格或矩阵,其中写入整数。但是,在任何情况下都不能安装它们;必须遵守一系列规则:
- 所有幻数和(任何水平、垂直或对角线的所有值的总和)必须始终给出与幻数常数相等的值(它是单个值)。
- 任何数字都不能重复两次。
- 您只能使用连续的数字(例如,从 1 到 9)或遵循特定系列的数字,例如:奇数、5 的倍数等。
另外,需要强调的是,我们可以根据正方形的结构对它们进行不同的分类。第一个是根据正方形的度数,相当于一行或一列中的单元格数量。第二是根据表的度数类型(偶数或奇数)。根据这些区别,我们可以将所有方块组织成不同的类别,尽管我们稍后将对此进行详细说明。
如何解决幻方问题?
为了解决这个数学游戏,我们可以使用两种不同的方法:使用几何或计算魔法常数。这两种程序同样有效,尽管一种可以让您更快地获得结果,而另一种则需要更多的时间和推理。接下来,我们将对这两种方法进行解释,以便您可以选择您喜欢的一种,并且可以更好地适应每种情况。
幻方的公式是什么?
第一种方法包括计算魔法常数,为此我们必须使用以下公式:n(n 2 +1)/2,其中 n 是平方的次数。一旦我们有了这个值,剩下的就是尝试不同的数字组合,这使我们能够将整个平方的幻数和等于常数。换句话说,我们需要形成加起来等于常数值的数字组合,从而使整个画面保持平衡。
如何使用几何来解幻方?
其次,我们可以使用几何来求解幻方。虽然需要注意的是,这种方法非常简单,不需要你锻炼你的计算能力,因为它纯粹是有条理的。话虽这么说,我们将解释求解偶数阶平方和奇数阶平方的过程。
如何解奇数幻方?
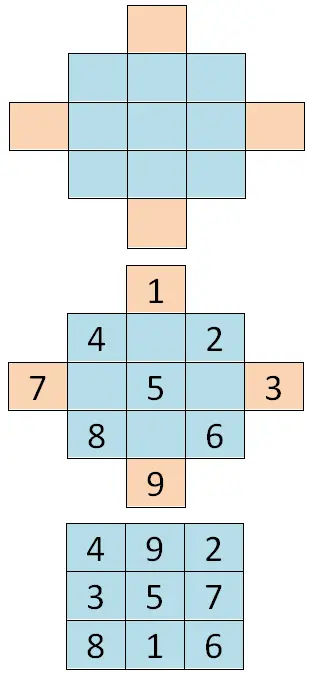
要解决第一种情况,您必须将单元格添加到初始表中,以便具有菱形排序。然后我们必须写出从该系列的第一个数字(在我们的例子中为 1)开始的所有连续数字,并且我们将沿着菱形的对角线移动。最后,我们需要将数字“加倍”,因此外部单元格的值会转到相反的一侧。所以垂直轴的外部单元格相交,那么水平轴的单元格也会发生同样的事情,下面你可以看到一个例子:
如何解偶数阶幻方?
为了求解偶数阶幻方(具有偶数行和偶数列的幻方),我们可以采用一种与之前的方法有些不同但也是基于几何的方法。我们首先在左上角写下该系列的第一个数字(在我们的例子中为 1)。然后,我们将遍历两条主对角线,并写入每个框的位置对应的值。
一旦我们写出了两条主对角线,我们就必须把自己放在从右下角开始的第一个空盒子里(在我们的例子中是盒子 15)。在那里,我们将写入该系列的第二个值,然后按顺序(从最小到最大)写入剩余的值,从右到左、从下到上完成单元格。为了更清楚地说明这一点,您可以使用我们向您展示的图片来定位自己:
如何构建魔方?
要自己构建幻方,我们可以遵循几个步骤,其中我们将重点介绍两个。应该注意的是,每种方法都将用于创建不同类型的方块,因此您必须根据要生成的方块仔细选择方法:
连体法
第一种方法非常简单,专门帮助我们构造任意大小的奇数幻方。遵循的过程非常简单,基本上我们将在第一行的中央框中写下该系列的第一个数字。从那里,我们将按照我们选择的算术级数的顺序返回,将下一个数字写在右边。然而,如果这个位置在绘制的正方形之外,我们将不得不移动到最后一行或最后一列。如果我们最终得到一个完整的正方形,我们将不得不从我们输入的最后一个数字正方形向下一个正方形,然后我们将以同样的方式继续。
下面您可以看到 3×3 的示例:
Strachey 幻方法
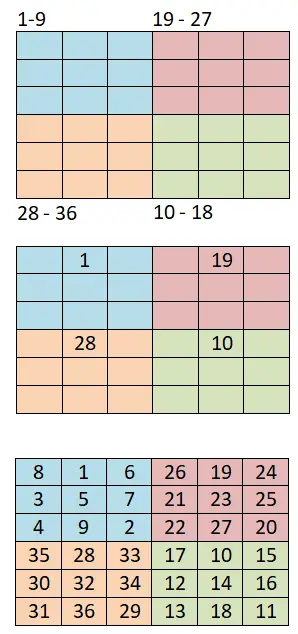
为了生成4k + 2 对 阶的幻方,我们将使用另一种方法,该方法基于前一种方法(连体方法),而且也非常简单。您可以在下面看到要遵循的步骤以及 6×6 幻方的有效示例:
- 分成更小的象限:我们需要做的第一件事是将棋盘细分为更小的正方形,例如,如果我们有一个 6×6 的棋盘,我们需要制作四个相等的 3×3 正方形象限。
- 使用连体方法:然后我们将为每个小象限分配一个数字范围,例如,如果我们以 1 开始序列,则范围将为:1-9(第一)、10-18(第四)、19-27 (第二)和 28-36(第三)。
康威幻方的 LUX 方法
当我们想要生成4n + 2 阶幻方时,我们将使用后一个系统,其中 n 是自然数。因此,我们创建这种样式的正方形的过程如下:
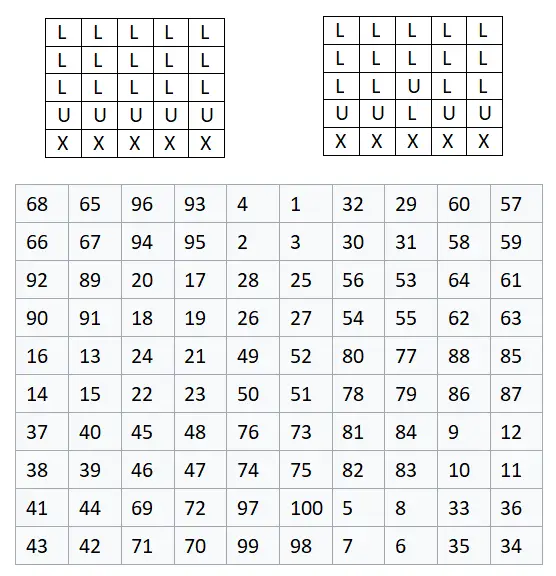
- 创建表或矩阵:我们首先创建一个 2n + 1 次的矩阵,其中 n 是自然数。有了这个,我们就可以设计桌子了,我们会记住它的程度,然后开始设计。
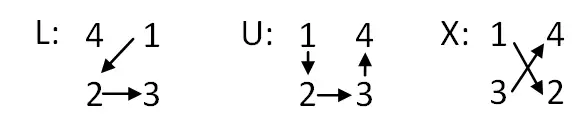
- 字母的位置:表格建好后,你必须从上到下写:n + 1行L,1行U和n – 1行X。然后,你必须交换U位于中间,L位于顶部。
- 将字母替换为数值:现在我们需要将字母替换为四个连续数字的组。根据字母的不同,我们会对数字给出一种或另一种顺序。解释如下:
我们首先构建一个5×5 矩阵,因此 n = 2,因为: 2n + 1 = 2 · 2 + 1 = 5。这意味着矩阵最终的大小将为 10×10,因为我们我们已经说过,每个包含字母的单元格相当于一组四个数字,即一个2×2的矩阵。下面您可以看到完成的示例,其中我们按照图中所示的顺序将每个字母替换为一组四个数字:
幻方练习
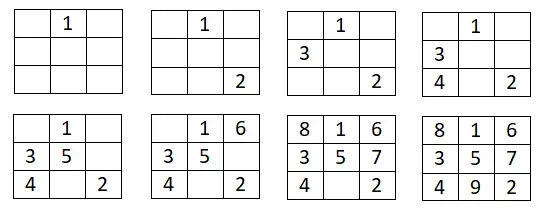
接下来,我们为您提供一些不完整的幻方,您必须自己填充它们,这要归功于我们在本文中解释的概念。请记住,您可以使用所教授的任何方法。此外,您需要考虑到 1 可能不是该系列中的第一个数字,尽管它会将其放入声明中。当您完成其中一项练习时,您将能够在语句下方看到解决方案。
3×3 幻方
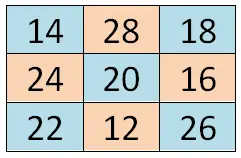
构造一个仅包含奇数的 3×3 幻方:
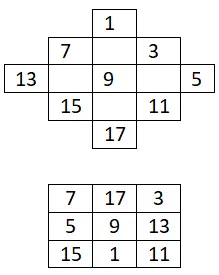
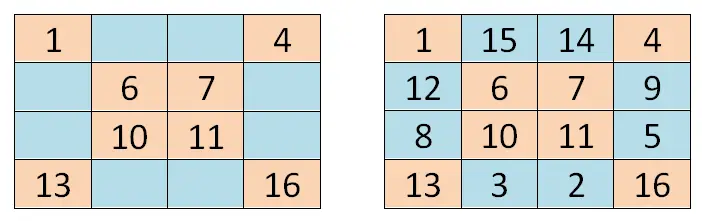
4×4幻方
完成以下 4×4 幻方:
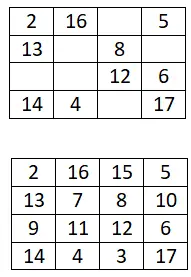
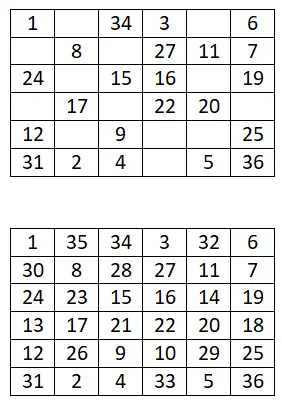
5×5幻方
完成以下 5×5 幻方:
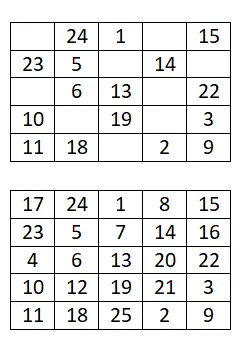
6×6 幻方
完成以下 6×6 幻方: