解释如何计算隐式平面方程(公式),也称为一般方程或笛卡尔方程。此外,您还将了解如何从平面的法向量找到平面的方程。而且,更重要的是,您将能够看到逐步解决的示例和练习。
该计划的隐式或一般方程是什么?
在解析几何中,平面的隐式方程,也称为平面的一般方程或笛卡尔方程,是允许任何平面以数学方式表达的方程。为了找到平面的隐式或一般方程,我们需要一个点和两个属于该平面的线性独立向量。
计划的隐式或一般方程的公式
考虑平面的一个点和两个方向向量:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
平面的隐式、一般或笛卡尔方程通过求解以下行列式并将结果设置为 0 来获得:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
因此,所得计划的隐式或一般方程如下:
![]()
重要的是,公式中的两个向量彼此线性无关,即它们必须具有不同的方向。为了满足这个条件,两个向量不平行就足够了。

虽然没有必要知道这个公式的原因,但您可以在下面看到它的演示。
从计划的参数方程开始,我们将继续讨论计划的隐式(或一般)方程:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46f87775f11f01a59c70aa3ee864aebe_l3.png)
首先,我们将每个参数方程的独立项传递到方程的另一边:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c2f3831ca03939d7e23d24c7d435337_l3.png)
或同等学历:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aca0b16ff9b92401181c2bdc5ba981bf_l3.png)
为了使上述方程组有可行解,以下矩阵的秩必须等于 2(Rouche-Frobenius 定理):
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f802b760ba5ab681afd0f02c83eddb6_l3.png)
因此,如果前一个矩阵的范围必须为 2,则 3×3 行列式必须等于 0:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
通过求解这个行列式,我们得到平面的一般、隐式或笛卡尔方程:
![]()
所以,我们刚刚看到了平面的隐式(或一般)方程和参数方程,但是,还有更多的方法可以解析地表达平面,例如矢量方程和规范方程。您可以在此链接中查看计划中所有方程的公式和解释。
如何找到平面的隐式或一般方程的示例
我们通过一个例子来看看如何确定平面的隐式(或一般或笛卡尔)方程:
- 求通过该点的平面的隐式或一般方程
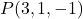
并包含向量
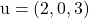
和
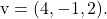
为了计算平面的一般或隐式方程,需要求解由两个向量、变量和点的坐标形成的以下行列式:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
因此,我们将向量和点代入公式:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa25223c3a00e31f89043a3500d32c68_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-7886f1c2758c204802b96f44acc8a7cd_l3.png)
现在我们求解 3 阶行列式,例如使用 Sarrus 规则或通过辅因子(或副因子):
![]()
现在我们对术语进行操作和分组:
![]()
![]()
![]()
因此,该计划的隐式或一般方程为:
![]()
从平面的法向量计算平面的隐式或一般方程
平面方程中一个非常典型的问题是在给定点及其法向(或垂直)向量的情况下找到给定平面的方程。那么,让我们看看它是如何工作的。
但您必须首先知道垂直于平面的向量的分量 X、Y、Z分别与该平面的隐式(或一般)方程的系数 A、B、C 一致。
![]()
金子
![]()
是与平面正交的向量
![]()
一旦我们知道了前面的关系,让我们看一个解决此类平面方程问题的例子:
- 确定通过该点的平面的隐式或一般方程
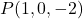
它的法向量之一是
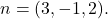
平面的隐式、一般或笛卡尔方程的公式为:
![]()
因此,从法向量中,我们可以找到系数 A、B 和 C,因为它们相当于法向量的分量:
![]()
而我们只需要找到参数D即可。为此,我们将属于平面的点的坐标代入方程:
![]()
![]()
![]()
![]()
![]()
因此该计划的隐式或一般方程为:
![]()
解决了平面隐式或一般方程的问题
练习1
求通过该点的平面的隐式或一般方程
![]()
并包含向量
![]()
和
![]()
为了计算平面的一般或隐式方程,需要求解由两个向量、三个变量和点的坐标组成的以下行列式:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
因此,我们将向量和点代入公式:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
现在我们用您选择的方法求解 3×3 矩阵的行列式:
![]()
最后,我们执行操作并对相似项进行分组:
![]()
![]()
![]()
因此该计划的隐式或一般方程为:
![]()
练习2
判断点是否
![]()
属于以下计划:
![]()
对于位于平面上的点,必须验证其方程。因此,我们需要将点的笛卡尔坐标代入平面的方程中,并检查方程是否成立:
![]()
![]()
![]()
![]()
![]()
该点不遵守平面方程,因此它不是该平面的一部分。
练习3
找到包含以下三点的计划的隐式(或一般)方程:
![]()
为了找到平面的隐式方程,我们需要找到两个绑定在平面上的线性无关向量。为此,我们可以计算由 3 个点定义的两个向量:
![]()
![]()
找到的两个向量的坐标不成比例,因此它们实际上是彼此线性独立的。
现在我们已经知道了平面上的两个方向向量和一个点,因此我们已经可以应用平面一般方程的公式:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
我们将向量和三个点之一代入公式:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-383093e607bc8ecc5f99e1815242b22a_l3.png)
最后,我们求解行列式:
![]()
![]()
![]()
![]()
简而言之,所讨论的平面的隐式、一般或笛卡尔方程为:
![]()
练习4
计算通过该点的空间平面的隐式或一般方程
![]()
它的法向量之一是
![]()
平面的隐式、一般或笛卡尔方程的公式为:
![]()
那么,从法向量中我们可以找到系数 A、B 和 C,因为它们分别等于法向量的分量:
![]()
所以我们只需要找到参数D即可。为此,我们将属于平面的点的坐标代入方程:
![]()
![]()
![]()
![]()
![]()
总之,该计划的隐式或一般方程为:
![]()