在这里您将了解什么是多项式函数以及什么是所有类型的多项式函数。此外,我们还解释了多项式函数的性质。
什么是多项式函数?
多项式函数是代数表达式为多项式 的函数,即多项式函数由有限个不同次数项的加法或减法定义。
因此,多项式函数可以通过以下表达式进行数学描述:
![]()
另一方面,多项式函数也可以使用以下公式定义:
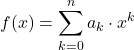
其中条款
![]()
和
![]()
分别是形成多项式函数的每个单项式的系数和变量。
期限
![]()
称为主项,表示多项式函数的次数,因为它是函数的最高次数单项式。换句话说,最大值指数是表示多项式函数次数的指数。
虽然我们会在下面看到更多多项式函数的特性,但任何多项式函数的定义域都是实数。
多项式函数的类型
给出多项式函数的定义,我们现在将了解所有类型的多项式函数都存在什么。
常数函数
常数函数是 0 次多项式函数,因此它是一种对于自变量 (x) 的任何值都始终采用相同图像的函数。
常数函数的一般表达式如下:
![]()
例如,以下三个函数是常数或零次多项式函数:
![]()
常数函数的图形表示是一条水平线(平行于 x 轴),其值等于常数。

您可以在以下链接中查看有关此类功能的更多功能:
➤参见:常数函数的特征
线性函数
线性函数也称为仿射函数,是一次多项式函数。因此,这种类型的多项式函数只能由线性项和独立项组成:
![]()
金子
![]()
是直线的斜率,
![]()
是 y 轴截距,即函数与 Y 轴相交的位置。
线性函数或一次多项式函数的示例:
![]()
有些人根据函数是否具有作为其项来区分线性函数和仿射函数
![]()
或不,是带截距的仿射函数和不带截距的线性函数。
线性函数的图形表示始终是直线,其倾斜度取决于函数斜率的值。
下面您可以图形化地看到一次多项式函数
![]()

然而,要绘制线性函数的图表,您需要清楚几个概念。在以下链接中,您将找到如何绘制此类多项式函数的分步说明:
➤请参阅:线性函数的图形表示
二次函数
二次函数是 2 次多项式函数,即高次项为二次的函数。
因此,二次函数的公式为:
![]()
金子
![]()
是二次项,
![]()
线性项和
![]()
多项式函数的独立项。
二次函数或二次多项式函数的示例:
![]()
二次函数的图形始终是抛物线,其形状取决于首项系数的符号。
![]()
- 如果系数

为正,二次函数是凸函数(形状像

)。
- 相反,如果系数

为负,二次函数是凹的(形状像

)。


因此,通过二次多项式函数主系数的符号,我们可以知道其图形将采取的形状,但为了使其精确的图形表示,必须遵循特定的程序。您可以在以下链接中查看此过程:
➤请参阅:二次函数的图形表示
三次函数
三次函数是三次多项式函数。因此,此类多项式函数的代数表达如下:
![]()
三次函数或三次多项式函数的示例:
![]()
![]()
三次函数的图形表示对应于三次曲线。然而,要在图中表示此类函数,必须遵循复杂的过程(其中包括导数)。您可以在这里查看它是如何完成的:
➤请参阅:如何表示函数
正如您所看到的,多项式函数的类型实际上是无限的,因为多项式可以有无限项。例如,四次函数类似于三次函数,但添加了二次项。重要的是您要了解多项式函数的类型是由函数的次数来标记的。
多项式函数的性质
多项式函数具有以下特点:
- 任何多项式函数的定义域都是实数集。
![]()
- 所有多项式函数都是连续的。
- 次数大于 1 的多项式函数没有渐近线。
- 无论多项式函数是什么类型,与纵坐标轴(Y 轴)的唯一交点位于其独立项的高度处,即在以下点处:
![]()
- 另一方面,多项式函数与横坐标轴(X 轴)相交的次数最多与函数的次数一样多。
- 如果多项式函数仅具有偶次项,则意味着它关于 OY 轴对称。另一方面,如果多项式函数仅具有奇数次项,则意味着该函数关于坐标原点对称。
- 多项式函数的相对极值(最大值或最小值)的个数至多为该函数的多项式负1的次数。
- 多项式函数的拐点数量最多等于该函数的多项式次数减 2。
- 可以使用多项式函数执行运算:
- 两个多项式函数的和给出另一个多项式函数。
- 两个多项式函数的乘积产生另一个多项式函数。
- 将多项式函数乘以标量(实数)会产生类似的多项式函数,但其图形会缩小或展开。
- 两个多项式函数的复合等于另一个多项式函数。