在本文中,我们解释什么是反函数(或倒数)以及如何计算函数的反函数。您还将了解如何轻松了解函数是否具有反函数以及此类函数的属性。最后,您可以通过反函数的分步练习进行练习。
什么是反函数?
反函数,又称倒函数,是指定义域为另一个函数(原函数)的值域,且其值域为原函数的定义域的函数。函数f的反函数用符号f -1表示。
因此, f(x)的反函数是满足以下条件的函数:
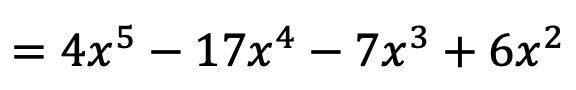
金子
![]()
是的反函数
![]()
反函数的概念也可以使用函数组合来定义,因为任何由其反函数组成的函数都等于恒等函数:
![]()
➤看: 什么是函数组合?
因此,如果前面的等式成立,则意味着
![]()
是以下函数的反函数(或倒数函数)
![]()
反函数示例
给出了反函数的定义,让我们解决一个例子以更好地理解它的含义。
- 判断下列函数是否互为反函数:
![]()
如果两个函数互为反函数,则满足以下2个条件:
![]()
因此,让我们检查两个方程是否都满足。我们首先检查
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \displaystyle\left(f \circ g\right)(x)& = f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x-1}{2} \right)\\[2ex]& = 2\left( \frac{x-1}{2} \right)+1\\[2ex]& =x-1+1\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-36f7d5f4d815a58f808114ae471c31dd_l3.png)
➤ 如果你不明白我们刚才的计算,你需要去上面的链接函数的组成是什么? ,我们解释一下如何用函数来解决此类操作。
以便
![]()
是的,已经完成了。 ✅
现在让我们检查一下相等性
![]()
![Rendered by QuickLaTeX.com \begin{aligned} \left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\Big(2x +1 \Big)\\[2ex]&=\cfrac{(2x+1)-1}{2}\\[2ex]&= \cfrac{2x}{2}\\[2ex]&=\bm{x} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83423fe7deab472f1a7e9575ec7af8c4_l3.png)
以及可逆性条件
![]()
这也完成了。 ✅
总之,由于两个方程都成立,因此这两个函数互为反函数。
您可以在下面看到这两个函数的图表。请注意,两个反函数的图形关于第一和第三象限的平分线对称:
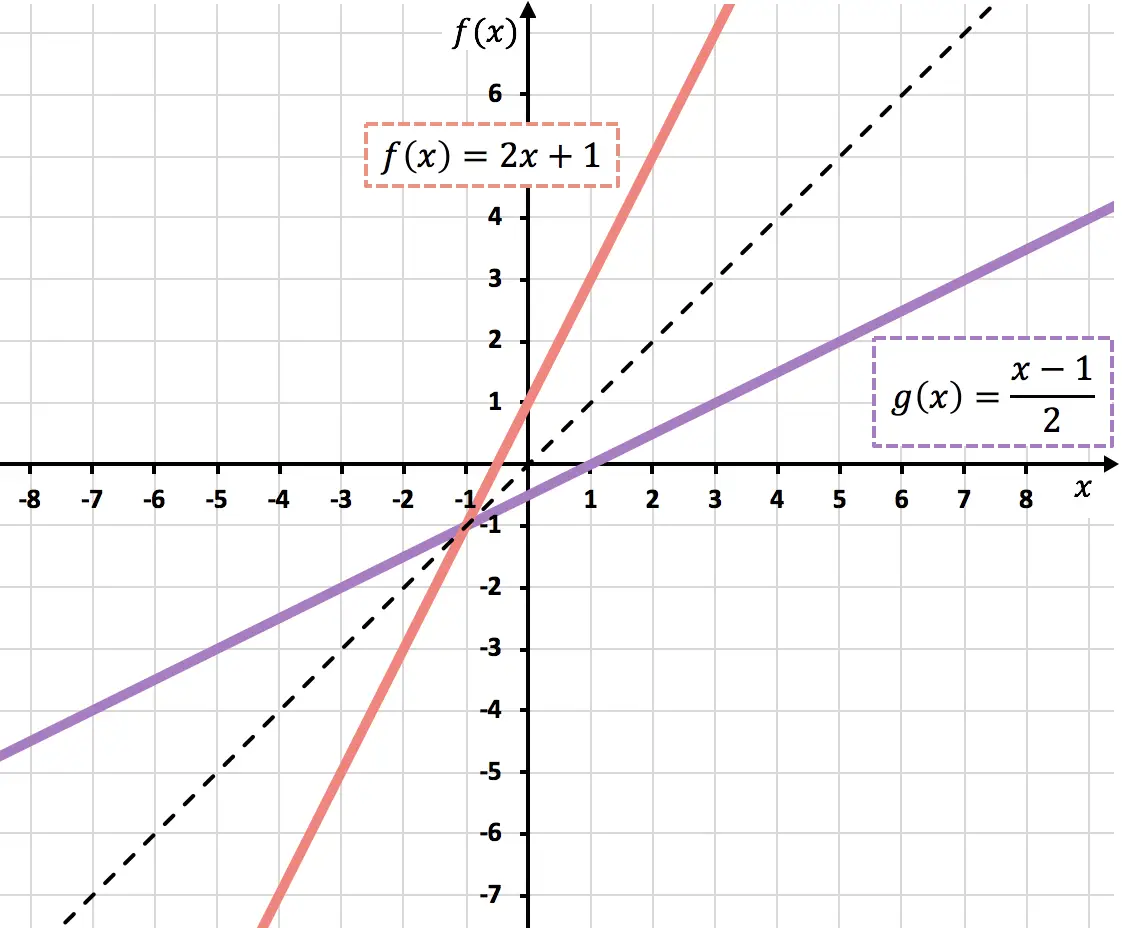
如何判断一个函数是否有反函数
如果一个函数是单射函数,即如果其整个域中的每个值对应于其区间中的单个值,则该函数具有反函数。
具有反函数的指数函数

无反函数的二次函数

例如,左指数函数具有反函数,因为每个x对应于f(x)的单个值。另一方面,右二次函数没有反函数,因为它有几个图像相等的x值(例如f(1)=f(3)=2) 。
类似地,双射函数由既是单射又是满射的函数组成,因此任何双射函数也有反函数。
另一方面,您应该记住,反函数与函数的乘法反函数不是一回事,而是两个不同的概念。要找到函数的乘法逆元,只需计算该函数的 1 个对应关系即可。
![]()
在下一节中,我们将了解如何确定反函数。
如何求反函数
要计算函数的反函数,必须执行以下步骤:
- 将f(x)替换为y 。
- 将所有x更改为y ,反之亦然。
- 清除y变量。
- 将变量y替换为f -1 (x) 。反函数是f -1 (x)的表达式。
为了让您清楚地了解反函数是如何计算的,我们将以确定以下函数的反函数为例:
![]()
首先我们需要更换
![]()
为了
![]()
:
![]()
现在我们改变一切
![]()
函数的
![]()
,反之亦然:
![]()
然后我们清除变量
![]()
![]()
![]()
![]()
![]()
最后,反函数
![]()
是我们通过分离得到的代数表达式
![]()
![]()
反函数练习题解答
下面我们准备了几个关于反函数的分步练习,以便您练习。
👉 请记住,如果您不明白如何解决练习或希望我们为您解决问题,您可以在评论中给我们写信!
练习1
检查以下两个函数是否互逆(或倒数):
![]()
要使两个函数互为反函数,必须满足以下条件:
![]()
因此有必要检查这两个条件是否满足。我们首先检查
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\left(f \circ g\right)(x)&= f\Big(g(x)\Big)\\[2ex]&= f\left( \frac{x+7}{3} \right)\\[2ex]&= 3 \left(\frac{x +7}{3} \right) - 7 \\[2ex] & =x + 7 - 7 \\[2ex]&= \bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-fbbdf5bb2c308a1973c5f2d99e822ad5_l3.png)
然而,
![]()
是的,已经完成了。 ✅
现在让我们检查一下函数的其他组成
![]()
![Rendered by QuickLaTeX.com \begin{aligned}\left(g \circ f\right)(x)&= g\Big(f(x)\Big)\\[2ex]&= g\left(3x-7\right)\\[2ex]&=\cfrac{(3x-7)+7}{3}\\[2ex]&=\cfrac{3x}{3}\\[2ex]&=\bm{x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ac5819584c8358b812c8214a902e4f08_l3.png)
借此
![]()
这也完成了。 ✅
这是怎么回事
![]()
和
![]()
,这两个函数互为反函数。
练习2
计算以下一次多项式函数的反函数(或倒数函数):
![]()
要反转该函数,首先要做的就是替换项
![]()
为了
![]()
![]()
现在我们改变
![]()
经过
![]()
,反之亦然:
![]()
然后我们释放
![]()
![]()
![]()
![]()
![]()
我们已经成功发布了
![]()
。因此,反函数
![]()
东方:
![]()
练习3
对以下二次多项式函数求逆:
![]()
为了找到反函数,我们将遵循上面看到的过程。所以我们会打电话
![]()
到函数
![]()
![]()
其次,我们修改
![]()
为了
![]()
,反之亦然:
![]()
最后,我们隔离变量
![]()
![]()
![]()
![]()
![]()
然而,在这种情况下,获得的函数对于其域的每个元素都有两个图像(正图像和负图像)。因此,问题函数不存在反函数。
练习4
确定以下有理函数的反函数(或倒数函数):
![]()
首先,我们替换
![]()
为了
![]()
![]()
现在我们改变
![]()
分子和分母
![]()
,反之亦然:
![]()
然后我们释放
![]()
![]()
表达方式
![]()
除掉方程的整个右侧,因此我们可以通过乘以方程的整个左侧来乘以它:
![]()
![]()
我们将所有条款与
![]()
等式的一侧,其他项在另一侧:
![]()
为了清除
![]()
,我们从等式左边提取公因数:
![]()
而作为一名邮递员
![]()
是将等式的整个左边相乘,我们可以通过除整个右边来做到这一点:
![]()
我们已经成功发布了
![]()
。所以反函数为
![]()
东方:
![]()
反函数的性质
反函数有以下特点:
- 反函数是唯一的,即如果一个函数是可逆的,则该函数只有一个反函数。
- 反函数的定义域是原函数的值域(或值域)。
- 同样,反函数的路径相当于原函数的定义域。
- 任何由其反函数组成的函数都给出恒等函数(x)。
![]()
- 函数的图像及其反函数的图像关于第一象限和第三象限的平分线对称。
- 反函数的反函数等于原函数:
![]()
- 对复合函数求逆相当于分别计算每个函数的反函数,然后将反函数复合起来。
![]()
- 一个函数与其反函数同时连续,或者换句话说,如果一个函数是连续的,那么它的反函数也是连续的。
- 如果函数可微并且导数在任何时候都不会消失
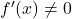
,它的反函数也是可微的。
另外,反函数的导数可以应用反函数定理计算,其公式为:
![]()