在此页面上,您将找到有关双曲正切的所有内容:它的公式是什么、它的图形表示、它的所有特征……
双曲正切公式
双曲正切函数是主要双曲函数之一,用符号tanh(x)表示。从数学上讲,双曲正切等于双曲正弦除以双曲余弦。
![]()
![]()
因此,双曲正切函数与指数函数有关。在以下链接中,您可以看到这些类型的函数的所有特征:
➤参见:指数函数的特征
双曲正切的图形表示
从它的公式中,我们可以图形化地表示双曲正切函数:
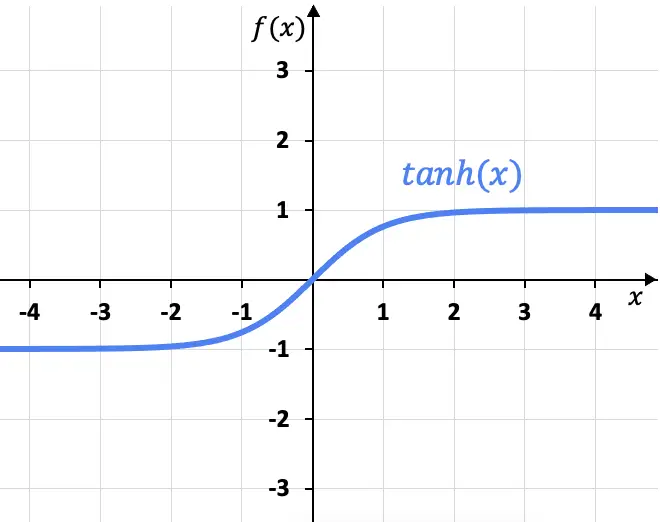
从图中可以看出,双曲正切函数在 x=+1 和 x=-1 处有两个水平渐近线,因为当 x 接近正无穷大时,函数的极限给出 x=+1,而极限为负无穷大给出 x=-1。
另一方面,双曲正切的图形与正切(三角函数)的图形无关,后者是周期函数。您可以在以下链接中查看正切的图形表示以及它与双曲正切的区别:
➤请参阅:正切函数的图形表示
双曲正切的特征
双曲正切函数具有以下性质:
- 双曲正切函数的定义域都是实数。
![]()
- 相比之下,双曲正切函数的路径或范围仅限于-1和+1(不包括在内)之间的值。
![]()
- 双曲正切是一个连续的双射奇函数(关于坐标原点对称)。
![]()
- 该函数在坐标原点处与 X 轴和 Y 轴相交。
![]()
- 双曲正切函数的正负无穷大的极限为+1/-1。因此,该函数在 x=+1 处有一个水平渐近线,在 x=-1 处有另一个水平渐近线。
![]()
![]()
- 双曲正切在其整个域上严格递增,因此它没有相对极值(既不是最大值也不是最小值)。
- 然而,函数在 x = 0 处由凸变为凹,因此 x = 0 是函数的拐点。
- 双曲正切函数的反函数称为双曲正切(或双曲反正切)参数,其公式如下:
![]()
- 双曲正切函数的导数是 1 除以双曲余弦的平方:
![]()
- 双曲正切函数的积分是双曲余弦的自然对数:
![]()
- 两个不同数字之和的双曲正切可以通过应用以下等式计算:
![]()
- 泰勒多项式或双曲正切级数具有收敛半径
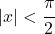
并对应于以下表达式:
![]()
金子
![]()
是伯努利数。