在这里,我们解释如何导出函数的双曲余切值。您还可以找到双曲余切值导数的示例。
双曲余切值的导数公式
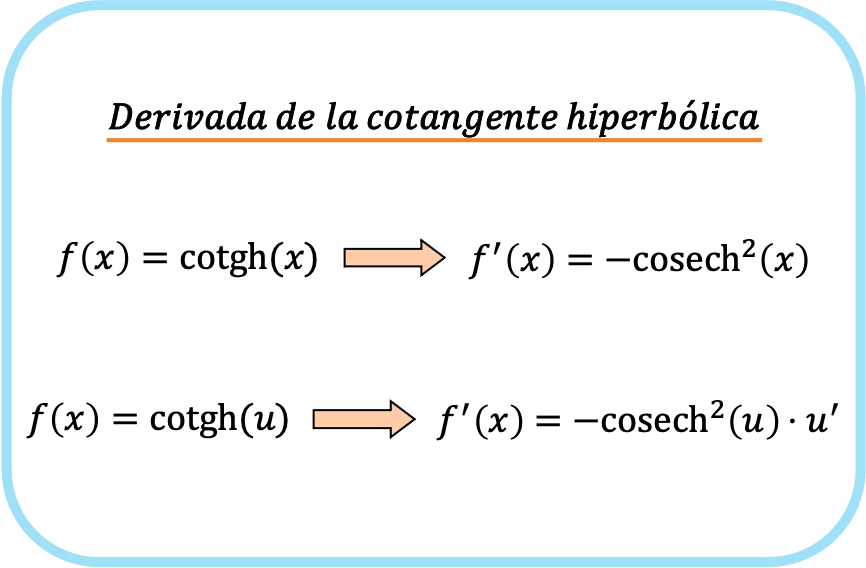
x 的双曲余切值的导数等于减去 x 的平方的双曲余割值。
![]()
因此,函数双曲余切的导数减去函数的双曲余割乘以该函数的导数。
![]()
请记住,在第二个公式中应用了链式法则,并且当双曲余切参数中存在 x 以外的函数时,将使用该公式。
您可能会在一些数学书籍中发现余切的导数是另一个,因为以下三个表达式是等效的:
![]()
显然,您可以使用这三个表达式中的任何一个来导出双曲余切值,但最常用的是双曲余割平方。
双曲余切导数的示例
一旦我们知道了函数双曲余切值的导数公式是什么,我们就可以求解此类三角导数的几个例子。
实施例1
在这个例子中,我们将看到函数 2x 的双曲余切值的导数是什么。
![]()
在双曲余切参数中,我们有一个 x 以外的函数,因此我们需要使用带有链式法则的公式来进行推导:
![]()
由于 2x 是一次项,其导数为 2。因此,要求 2x 双曲余切的导数,我们只需将 2x 放入双曲余割的平方参数中,然后乘以 2。
![]()
实施例2
在第二个示例中,我们将确定多项式函数双曲余切值的导数值。
![]()
正如我们在上面看到的,导出函数双曲余切的规则如下:
![]()
因此,本练习的双曲余切值的导数如下:
![]()