在此页面中,您将找到对正则或可逆矩阵的解释,以及如何知道何时可以执行矩阵的逆,何时不能执行。此外,您还将看到几个正则矩阵的示例,以充分理解该概念,最后,我们将向您展示此类矩阵的所有属性。
什么是正则矩阵?
正则矩阵的定义如下:
正则矩阵是可以求逆的方阵,即可以计算该矩阵的逆矩阵。因此,其行列式不为零 (0)。
正则矩阵也称为可逆矩阵、非奇异矩阵或非简并矩阵。
与正则矩阵相反的矩阵是奇异矩阵或简并矩阵。
因此,要知道什么时候一个矩阵是正则矩阵还是奇异矩阵,也就是说什么时候一个矩阵是可逆的,什么时候是不可逆的,只需求解该矩阵的行列式即可:
- 如果矩阵的行列式非零,则该矩阵是正则矩阵或可逆矩阵。
- 如果矩阵的行列式等于零,则该矩阵是奇异的或不可逆的。
总之,计算矩阵的行列式是了解矩阵是否有逆矩阵的最简单方法,因此我们建议用它来确定任何矩阵的可逆性。
如果你想知道如何求逆矩阵,你可以查看逆矩阵公式,它一步步解释了如何求逆矩阵,你还会找到几个例子和已解决的练习来练习。
正则矩阵或可逆矩阵的示例
了解了正则矩阵或可逆矩阵的含义后,让我们看一些不同维度正则矩阵的示例:
正则或可逆 2×2 矩阵的示例
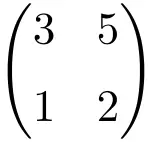
我们可以通过计算它的行列式来验证它是一个正则矩阵:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-9e4a833393b2e66b49eb3b434136b755_l3.png)
2阶矩阵的行列式不等于0,因此是正则矩阵。
正则或可逆 3×3 矩阵的示例
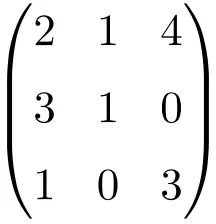
我们必须对矩阵求行列式来验证它是可逆矩阵:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c0389d86d007f9ee667b14c0071b6395_l3.png)
3阶矩阵的行列式给出的结果不为0,因此它是正则矩阵。
正则或可逆 4×4 矩阵的示例

对矩阵求行列式可知它是正则矩阵:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2a07b3fa1ed83267c0bc723dd027d724_l3.png)
4 阶矩阵的行列式不为零,因此它是可逆矩阵。
警告:如果您对行列式的计算有疑问,可以查阅如何计算行列式页面。
正则矩阵或可逆矩阵的性质
正则矩阵或可逆矩阵对于线性代数非常重要,这是由于以下特征:
- 如果 A 是可逆矩阵,那么它的转置或转置矩阵也是可逆矩阵。另外,转置的逆矩阵等于逆矩阵的转置。
![]()
- 正则矩阵的范围总是尽可能的最大值,或者换句话说,范围相当于矩阵的维数。
- 两个可逆矩阵之间的矩阵乘积产生另一个正则矩阵。这个条件可以很容易地用行列式的性质来证明:
![Rendered by QuickLaTeX.com \displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-88d940d46390d4f5f0d6e694ac5a18d5_l3.png)
- 每个正交矩阵同时也是一个正则矩阵。
- 设 A 为表示线性方程组的矩阵
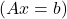
,如果A是正则矩阵,则系统有唯一解,因此是兼容行列式系统(SCD)。
- 此外,如果系统是同质系统
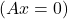
且 A 可以反转,系统的解很简单:
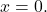
- 正则矩阵的列和行彼此线性独立。
- 正则或可逆矩阵的所有特征值(或特征值)均非零。