在此页面上,您将了解什么是 Gauss-Jordan 方法以及如何使用高斯方法求解方程组。此外,您还将找到使用高斯方法的系统的示例和已解决的练习,以便您可以完美地练习和理解它。
高斯法是什么?
Gauss-Jordan 方法是用于求解具有 3 个未知数的方程组的过程,也就是说:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 3x-4y+5z=10 \\[2ex] x+5y-2z=4 \\[2ex] -x+4y+2z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-088146ef83bbd007e82aca8189434c25_l3.png)
高斯方法的目标是将初始方程组转换为阶梯方程组,即每个方程的未知数都比前一个方程少的一个方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} a_1x+b_1y+c_1z=d_1 \\[2ex] a_2x+b_2y+c_2z=d_2 \\[2ex] a_3x+b_3y+c_3z=d_3 \end{array} \right\} \ \bm{\longrightarrow} \left. \begin{array}{r} A_1x+B_1y+C_1z=D_1 \\[2ex] B_2y+C_2z=D_2 \\[2ex] C_3z=D_3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-10926b0856ae512c737ae924bd9413a1_l3.png)
然而,要做到这一点,您必须首先知道如何以矩阵形式表达方程组以及该矩阵上允许的变换。所以我们之前会解释这两件事,然后我们会看到如何使用高斯方法程序。
系统扩展矩阵
在了解系统如何求解之前,您必须知道方程组可以用矩阵的形式表示:
![]()
放在第一列,系数
![]()
在第二列中,系数
![]()
第三列中的数字和第四列中没有未知数的数字。
例如:
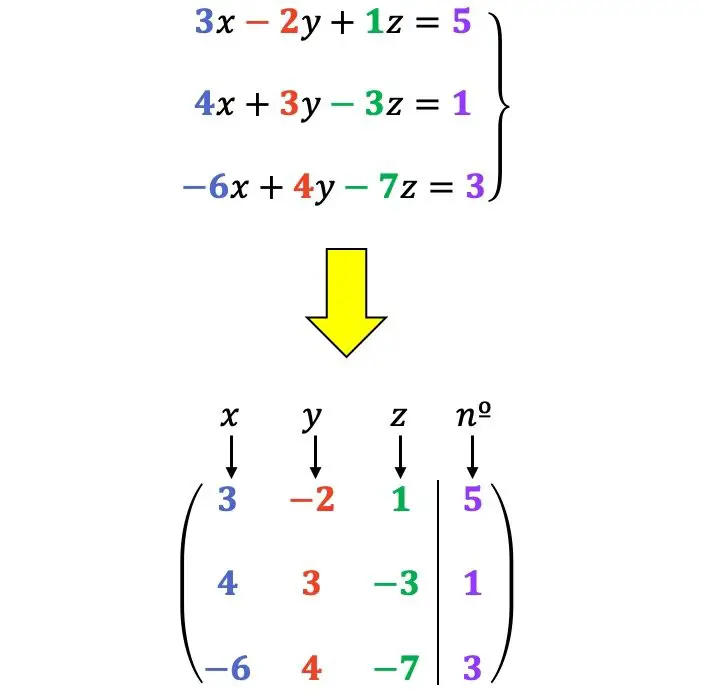
允许的行转换
为了将方程组转换为缩放系统,可以对与该系统相关的矩阵执行以下操作之一:
- 更改矩阵中的行顺序。
例如,我们可以更改矩阵第 2 行和第 3 行的顺序:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] -2 & 4 & -1 & 2 \\[2ex] 6 & 1 & -3 & 10 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{ f_2 \rightarrow f_3}} \\[2ex] \xrightarrow{ f_3 \rightarrow f_2}} \end{array} \left( \begin{array}{ccc|c} 3 & 5 & -2 & 1 \\[2ex] 6 & 1 & -3 & 10 \\[2ex] -2 & 4 & -1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ee0e251559ef9dfd02c9b0105f934af8_l3.png)
- 将一行中的所有项乘以或除以0 以外的数字。
例如,我们可以将第 1 行乘以 4,并将第 3 行除以 2:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & 3 & 1 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 2 & -4 & -2 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{4 f_1} \\[2ex] \\[2ex] \xrightarrow{ f_3 / 2} \end{array} \left( \begin{array}{ccc|c} 4 & -8 & 12 & 4 \\[2ex] 3 & -1 & 5 & -3 \\[2ex] 1 & -2 & -1 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-0e1f081c9056075ede064b2e5c9e4193_l3.png)
- 将一行替换为同一行加上另一行乘以一个数字的总和。
例如,在以下矩阵中,我们将第 2 行与第 3 行相加并乘以 1:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 2 & 4 & 1 & -5 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + 1 \cdot f_3} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} -1 & -3 & 4 & 1 \\[2ex] 3 & 2 & 4 & -6 \\[2ex] 1 & -2 & 3 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-04417e2094ac05c7a374334c55197f36_l3.png)
如何使用高斯方法求解方程组?
现在我们将通过一个例子来了解用高斯方法求解方程组的过程:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} -x+2y+2z=-24 \\[2ex] x+y+z=48 \\[2ex] 2x-6y+4z=12 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-61e6e829301e6730c9e27f9c0a30de2e_l3.png)
首先要做的是系统的扩展矩阵:
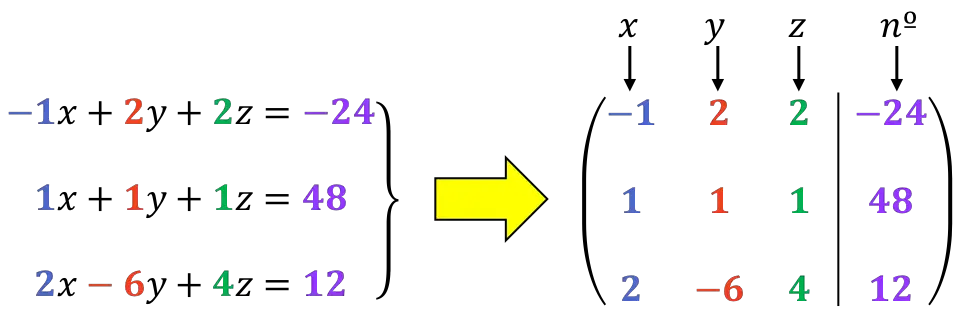
正如我们稍后将看到的,第一行的第一位数字最好是 1。因此,我们将更改第 1 行和第 2 行的顺序:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} -1 & 2 & 2 &-24 \\[2ex] 1 & 1 & 1 & 48 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \xrightarrow{ f_1 \rightarrow f_2} \\[2ex] \xrightarrow{ f_2 \rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} \color{blue}\boxed{\color{black}1} & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 &-24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b45e0f757ca2880442314f6a4800697b_l3.png)
高斯方法的目标是使主对角线以下的数字为 0 。也就是说,我们需要将红色数字转换为0:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{red}\bm{-1} & 2 & 2 &-24 \\[2ex] \color{red}\bm{2} & \color{red}\bm{-6} & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-28164ac6b48d32c09b4725548c0633f6_l3.png)
为了消除这些数字,我们需要对行执行适当的转换。
例如,第二行第一个元素 -1 是第一行第一个元素 1 的负数。因此,如果我们将第一行添加到第二行, -1 将被消除:

因此,如果我们进行求和,我们最终会得到以下矩阵:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] -1 & 2 & 2 & -24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 + f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] \color{blue}\boxed{\color{black}0} & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b106306b92bfc3e99d602c22d5198bd_l3.png)
这样我们就成功地将-1 转化为0。
现在我们要转换 2。如果您注意到,第三行中的第一个元素 2 是第一行中的第一个元素 1 的两倍。因此,如果我们将第一行乘以 -2 添加到第三行,则2 将被消除:
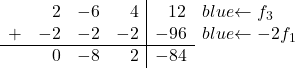
因此,我们最终得到以下矩阵:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 2 & -6 & 4 & 12 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_1} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] \color{blue}\boxed{\color{black}0} & -8 & 2 & -84 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-36b2fdf8de855cf35049ecefcf7c1da5_l3.png)
这样我们就成功地将2变成了0。
我们现在要做的就是将 -8 转换为 0。为此,我们将第三行乘以 3,然后将第二行乘以 8:
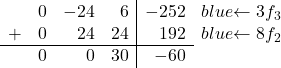
因此我们得到以下矩阵:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & -8 & 2 & -84 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{3f_3 + 8f_2} \end{array} \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & \color{blue}\boxed{\color{black}0} & 30 & -60 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-6e2324629222c746a9021ce05ba7d54d_l3.png)
通过这些变换,我们将主对角线以下的所有数字都变为 0。现在我们可以求解方程组了。
我们现在必须将矩阵转换为具有未知数的方程组。为此,请记住第一列对应于
![]()
,第二列
![]()
,第三列
![]()
最后一列是没有未知数的数字:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & 1 & 48 \\[2ex] 0 & 3 & 3 & 24 \\[2ex] 0 & 0 & 30 & -60 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 1x+1y+1z=48 \\[2ex] 3y+3z=24 \\[2ex] 30z=-60 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f90de9d9f5a06959a2d4aebf05f4758_l3.png)
最后,为了求解系统,我们需要自下而上求解方程的未知数。由于最后一个方程只有一个未知数,我们可以求解它并找到它的值:
![]()
![]()
![]()
现在我们知道 z 是什么,如果我们将其值代入第二个方程,我们可以找到
![]()
:
![]()
![]()
![]()
![]()
![]()
![]()
我们对第一个方程做同样的事情:我们替换其他未知数的值并删除
![]()
:
![]()
![]()
![]()
![]()
因此,方程组的解为:
![]()
用高斯-乔丹法求解方程组问题
练习1
使用高斯方法求解以下方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-854043b0e7e3e2166593dcf5c645bfa0_l3.png)
我们首先要做的是系统的扩展矩阵:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} x+y-z=2 \\[2ex] x-2y+3z=0 \\[2ex] 2x-y+3z=3 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-1b6369a58b91f31bf4c8bc212ccf68c6_l3.png)
现在我们需要将主数组下面的所有数字都设为 0。
因此,我们执行行操作来取消第一列的最后两项:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 1 & -2 & 3 & 0 \\[2ex] 2 & -1 & 3 & 3 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -f_1} \\[2ex] \xrightarrow{f_3-2f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-cd42dcf61aebc4c67de13e09dff72f4b_l3.png)
现在我们从第二列中删除最后一个元素:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & -3 & 5 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-13945337848a6f1badf6efe249951124_l3.png)
一旦主对角线以下的所有数字都为 0,我们现在就可以求解方程组了。为此,我们再次以未知数方程组的形式表示矩阵:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 1 & -1 & 2 \\[2ex] 0 & -3 & 4 & -2 \\[2ex] 0 & 0 & 1 & 1 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+y-z=2 \\[2ex] -3y+4z=-2 \\[2ex] 1z=1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-f068c276aae018a668cc005bcad3e641_l3.png)
我们从下到上求解方程的未知数。我们首先求解最后一个方程:
![]()
![]()
现在我们将 z 的值代入第二个方程来求 y 的值:
![]()
![]()
![]()
![]()
![]()
我们对第一个方程做同样的事情:我们替换其他未知数的值并求解 x:
![]()
![]()
![]()
![]()
因此,方程组的解为:
![]()
练习2
使用高斯方法求以下方程组的解:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-7d0595899b8137f769c74fce1b21286b_l3.png)
我们首先要做的是系统的扩展矩阵:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+y+2z=-3 \\[2ex] x+3y+2z=5 \\[2ex] 4x+2y-z=-1 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-5e2a16b6d1451520bd8898675c022dc2_l3.png)
要应用高斯方法,如果第一行中的第一个数字是 1 会更简单。因此,我们将更改第 1 行和第 2 行的顺序:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 1 & 2 & -3 \\[2ex] 1 & 3 & 2 & 5 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \xrightarrow{f_1\rightarrow f_2} \\[2ex] \xrightarrow{f_2\rightarrow f_1} \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-ef7e2e42d0eecb0395afb7c8311b2ade_l3.png)
现在我们需要将主数组下面的所有数字都设为 0。
因此我们执行行操作来替换第一列的最后两个元素:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 2 & 1 & 2 & -3 \\[2ex] 4 & 2 & -1 & -1 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -2f_1} \\[2ex] \xrightarrow{f_3-4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-40baaee3bbde9ed1577e00bc1c3b338f_l3.png)
现在我们将第二列的最后一个元素转换为零:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & -10 & -9 & -21\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{f_3-2f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-f328906485bfe6ee77833c04869e1240_l3.png)
一旦主对角线以下的所有数字都为 0,我们就可以求解方程组。为此,我们再次以未知数方程组的形式表示矩阵:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & 3 & 2 & 5 \\[2ex] 0 & -5 & -2 & -13 \\[2ex] 0 & 0 & -5 & 5 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x+3y+2z=5 \\[2ex] -5y-2z=-13 \\[2ex] -5z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a7e129715c720218a5cb25ef07442442_l3.png)
我们从下到上求解方程的未知数。我们首先求解最后一个方程:
![]()
![]()
现在我们将 z 的值代入第二个方程来求 y 的值:
![]()
![]()
![]()
![]()
![]()
我们对第一个方程做同样的事情:我们替换其他未知数的值并求解 x:
![]()
![]()
![]()
![]()
因此,方程组的解为:
![]()
练习3
用高斯法计算下列方程组的解:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4301eae3179543fbdee7568e8f88aa4c_l3.png)
我们首先要做的是系统的扩展矩阵:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x+3y+z=-1 \\[2ex] 6x+4y+4z=0 \\[2ex] -4x+2y-z=5\end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c0d96160d6670e817dd39f61816e1e6e_l3.png)
现在我们需要将父数组下的所有数字都设为0。
因此我们执行行操作来替换第一列的最后两个元素:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 6 & 4 & 4 & 0 \\[2ex] -4 & 2 & -1 & 5\end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+2f_1} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-87853177b6be449178c24e414dc0865a_l3.png)
现在我们将第二列的最后一个元素转换为零:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 8 & 1 & 3\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+8f_2} & \end{array} \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-c4105ceb64b201c532109f8639bdefde_l3.png)
一旦主对角线以下的所有数字都为 0,我们就可以求解方程组。为此,我们再次以未知数方程组的形式表示矩阵:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 2 & 3 & 1 & -1 \\[2ex] 0 & -5 & 1 & 3 \\[2ex] 0 & 0 & 13 & 39\end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} 2x+3y+1z=-1 \\[2ex] -5y+z=3 \\[2ex] 13z=39 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-faae83295a3f7b3d8b6d76f78d56fac6_l3.png)
我们从下到上求解方程的未知数。我们首先求解最后一个方程:
![]()
![]()
现在我们将 z 的值代入第二个方程来求 y 的值:
![]()
![]()
![]()
![]()
我们对第一个方程做同样的事情:我们替换其他未知数的值并求解 x:
![]()
![]()
![]()
![]()
![]()
因此,方程组的解为:
![]()
练习4
使用高斯方法求解以下具有 3 个未知数的方程组:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b005b2eda0d63c7130f2f5531c2ae4a0_l3.png)
在应用高斯方法之前,我们需要排列方程组,使所有未知数位于方程左侧,数字位于右侧:
![Rendered by QuickLaTeX.com \left. \begin{array}{r}2x-6=4y+6z \\[2ex] -y-3z=1-3x \\[2ex] -4x-y=6-3z \end{array} \right\} \longrightarrow \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6\end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1e0ca77b625e8f9e235ce8da4e4008df_l3.png)
一旦系统被订购,我们就构建系统的开发矩阵:
![Rendered by QuickLaTeX.com \left. \begin{array}{r} 2x-4y-6z=6 \\[2ex] 3x-y-3z=1 \\[2ex] -4x-y+3z=6 \end{array} \right\} \longrightarrow \left( \begin{array}{ccc|c} 2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b88e3ff141b847028a55ba4b46b8e870_l3.png)
由于第一行中的所有数字都是偶数,因此在对行进行操作之前,我们将第一行除以 2。因为这将使计算更容易:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}2 & -4 & -6 & 6 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \xrightarrow{f_1/2} \\[2ex] \\[2ex] & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-b05235526cd8e44c16749606bfe8976c_l3.png)
现在我们需要将主数组下面的所有数字都设为 0。
因此我们执行行操作来替换第一列的最后两个元素:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 3 & -1 & -3 & 1 \\[2ex] -4 & -1 & 3 & 6 \end{array} \right) \begin{array}{c} \\[2ex] \xrightarrow{f_2 -3f_1} \\[2ex] \xrightarrow{f_3+4f_1} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-3da82815d14fdfae0f61a8e1747fb9fe_l3.png)
和之前一样,由于最后一行中的所有数字都是 9 的倍数,因此我们将其除以 9 以使计算更容易:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -9 & -9 & 18 \end{array} \right) \begin{array}{c} \\[2ex] \\[2ex]\xrightarrow{f_3/9} & \end{array} \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-342000d19a7bd19e055a39695c79cb49_l3.png)
现在我们将第二列的最后一个元素转换为零:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c}1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & -1 & -1 & 2\end{array} \right) \begin{array}{c} \\[2ex] \\[2ex] \xrightarrow{5f_3+f_2} & \end{array} \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right)](https://mathority.org/wp-content/ql-cache/quicklatex.com-2158e7f439f677617bb8a40695fb5711_l3.png)
一旦主对角线以下的所有数字都为 0,我们就可以求解方程组。为此,我们再次以未知数方程组的形式表示矩阵:
![Rendered by QuickLaTeX.com \left( \begin{array}{ccc|c} 1 & -2 & -3 & 3 \\[2ex] 0 & 5 & 6 & -8 \\[2ex] 0 & 0 & 1 & 2 \end{array} \right) \ \longrightarrow \ \left. \begin{array}{r} x-2y-3z=3 \\[2ex] 5y+6z=-8 \\[2ex] 1z=2 \end{array} \right\}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ea162e98aa70f8d56ffba28438a9de2a_l3.png)
我们从下到上求解方程的未知数。我们首先求解最后一个方程:
![]()
![]()
现在我们将 z 的值代入第二个方程来求 y 的值:
![]()
![]()
![]()
![]()
![]()
我们对第一个方程做同样的事情:我们替换其他未知数的值并求解 x:
![]()
![]()
![]()
![]()
因此,方程组的解为:
![]()