Sur cette page vous trouverez la formule du carré d’une somme, c’est-à-dire de l’identité notable (a+b) 2 . Vous pourrez également voir des exemples et des exercices résolus de sommes au carré. Et, en plus, vous découvrirez les propriétés géométriques que cache ce produit remarquable.
Qu’est-ce que le carré d’une somme ?
Le carré d’une somme est l’une des identités notables (ou produits notables), c’est donc une règle mathématique qui permet de calculer rapidement la puissance d’un binôme à deux termes positifs au carré.
Ainsi, le carré d’une somme est constitué de deux termes différents additionnés et élevés au carré, c’est-à-dire que l’expression algébrique du carré d’une somme est (a+b) 2 .
Formule du carré d’une somme
Etant donné la définition mathématique de ce type remarquable d’identité, nous allons maintenant voir quelle est la formule du carré d’une somme :

De sorte que le carré d’une somme est égal au carré du premier terme, plus le double du produit du premier par le second, plus le carré du second.
Ainsi, pour résoudre une somme au carré, il ne suffit pas d’élever chaque addition à deux, mais, en plus, les deux additions doivent être multipliées entre elles et par 2.
Il est important de s’en souvenir, car une erreur très courante lors de la somme des carrés est d’oublier le produit entre les deux termes et de ne calculer que les carrés :

N’oubliez pas de ne laisser aucun terme de la formule !
Par contre, rappelons que la formule d’une soustraction au carré (ou carré d’une soustraction) est très similaire à celle que nous venons de voir, mais elle a une différence qui change complètement le résultat. Si vous ne savez pas exactement à quoi cela ressemble, vous pouvez vérifier ici quelle est la formule de soustraction au carré et comment elle est appliquée.
Exemples de carrés de somme
Voici plusieurs exemples pratiques pour que vous puissiez voir comment faire le carré d’une somme :
Exemple 1
- Calculez la somme suivante au carré en appliquant la formule :
![]()
La formule d’une somme au carré est :
![]()
Il faut donc d’abord identifier les paramètres
![]() et
et![]() de la formule. Dans ce cas,
de la formule. Dans ce cas,![]() représente le
représente le![]() du binôme et
du binôme et![]() correspond au numéro 5 :
correspond au numéro 5 :
![Rendered by QuickLaTeX.com \left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5ba75b0f34f956985ea0163011a03acf_l3.png)
Eh bien, puisque nous connaissons maintenant les valeurs de
![]() et de
et de![]() On peut appliquer la formule pour trouver le résultat du carré de la somme :
On peut appliquer la formule pour trouver le résultat du carré de la somme :

Exemple 2
- Résolvez l’expression suivante pour le carré d’une somme :
![]()
La formule du carré d’une somme est :
![]()
Donc dans ce problème
![]() est le monôme
est le monôme![]() et d’autre part,
et d’autre part,![]() est le terme indépendant 4 :
est le terme indépendant 4 :
![Rendered by QuickLaTeX.com \begin{array}{c} a=3x \\[2ex] b=4 \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-89bb3514fbd79ba368588655e152e9cc_l3.png)
Enfin, une fois que nous avons identifié les valeurs de
![]() et de
et de![]() , on applique la formule d’une somme au carré pour résoudre le produit notable :
, on applique la formule d’une somme au carré pour résoudre le produit notable :
![Rendered by QuickLaTeX.com \begin{aligned} (3x+4)^2 & =(3x)^2+2 \cdot 3x\cdot 4+4^2 \\[2ex] & =9x^2+24x+16 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ed0d9fcdbeeac2247b68789dd0268f37_l3.png)
Preuve de la formule du carré d’une somme
Ensuite nous allons déduire la formule que nous venons de voir du carré d’une somme, pour que vous compreniez d’où elle vient.
Partant d’un binôme positif élevé au 2 :
![]()
La puissance ci-dessus est évidemment équivalente au facteur
![]() multiplié par lui-même :
multiplié par lui-même :
![]()
Donc, nous multiplions les deux parenthèses en utilisant la propriété distributive :
![Rendered by QuickLaTeX.com \begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-1c871c4ad6546c817128379acbef78c8_l3.png)
Enfin, à partir des termes résultants, nous regroupons ceux qui sont similaires :
![]()
Et nous sommes déjà arrivés à l’expression polynomiale de la formule, il est donc démontré :
![]()
Bien que cela puisse être difficile à croire, le carré d’une formule de somme fonctionne également pour factoriser des polynômes quadratiques . Au cas où vous ne sauriez pas ce que c’est, la factorisation polynomiale est une procédure souvent utilisée en mathématiques pour simplifier l’expression d’un polynôme. Découvrez comment cela se fait en cliquant sur le lien ci-dessus.
Interprétation géométrique du carré d’une somme
Jusqu’à présent, nous avons vu comment le carré d’une somme est calculé mathématiquement, mais ce produit remarquable peut également être interprété géométriquement.
Regardez le carré suivant dont les côtés mesurent
![]()
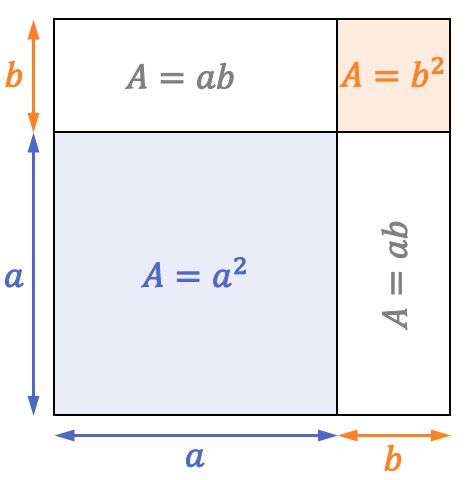
L’aire d’un carré est égale à la longueur d’un de ses côtés élevé au carré. Par conséquent, comme le côté du carré précédent est
![]() son aire (ou surface) est égale à
son aire (ou surface) est égale à![]()
Eh bien, comme vous pouvez le voir dans la représentation du carré, un carré d’une aire de
![]() rectangles à deux aires
rectangles à deux aires![]() et un autre carré de surface
et un autre carré de surface![]() Par conséquent, la formule de la somme d’un carré est également remplie d’un point de vue géométrique :
Par conséquent, la formule de la somme d’un carré est également remplie d’un point de vue géométrique :
![]()
Problèmes résolus du carré d’une somme
Ensuite, nous vous laissons avec plusieurs exercices résolus étape par étape de sommes de carrés afin que vous puissiez vous exercer et ainsi finir de comprendre le concept. Vous pouvez nous écrire toutes vos questions dans les commentaires, et nous nous ferons un plaisir d’y répondre. 💭💭💭
Exercice 1
Déterminez les sommes suivantes élevées au carré :
![]()
![]()
![]()
![]()
Pour résoudre toutes les identités notables du problème il suffit d’appliquer la formule du carré d’une somme :
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-571dada676a093b9b625887a09615b5c_l3.png)
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}(2+6x)^2 & =2^2+2\cdot 2\cdot 6x +(6x)^2\\[2ex] & = \bm{4+24x+36x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-8d696f9e8ea8a9246922a0aa132d7e24_l3.png)
![Rendered by QuickLaTeX.com \text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-62f7ef68fc47d45958f6a10dbfe3f512_l3.png)
![Rendered by QuickLaTeX.com \text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-2fdf798e7d585cdbc2bbeb0417bfc62a_l3.png)
Exercice 2
Résolvez les carrés somme suivants de deux termes en appliquant la formule :
![]()
![]()
![]()
Pour calculer tous les produits notables du problème il faut utiliser la formule d’une somme élevée au carré :
![]()
![Rendered by QuickLaTeX.com \text{A)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b8eaa03c68adc376819c5e12081f6d39_l3.png)
Dans la section B) vous devez vous rappeler que si une racine est élevée au carré, elle est simplifiée :
![Rendered by QuickLaTeX.com \text{B)} \ \begin{aligned}\left(\sqrt{2x}+\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2+2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x+2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x+2\sqrt{16x^2} \\[2ex] &= 10x+2\cdot 4x = \\[2ex] & = 10x +8x \\[2ex] & = \bm{18x}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-a38b1df7ca331cb002253d52eb008608_l3.png)
Les monômes de la dernière somme élevés au carré ont des coefficients fractionnaires, donc pour le résoudre, nous devons également utiliser les propriétés des fractions :
![Rendered by QuickLaTeX.com \text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-c50dcca740e334b34f746e71f4af826e_l3.png)
Exercice 3
Trouver la puissance suivante en appliquant la formule du carré d’une somme et sans utiliser la calculatrice :
![]()
Tout d’abord, le nombre dix-sept peut être décomposé en la somme de 10 plus 7 :
![]()
Nous avons donc converti la puissance en une somme au carré. Par conséquent, nous pouvons maintenant appliquer la formule correspondante :
![Rendered by QuickLaTeX.com \begin{aligned}(10+7)^2 & = 10^2+2\cdot 10 \cdot 7 +7^2 \\[2ex] & =100+140+49\\[2ex] & =289 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-83e35048f0ae6ae12bc2b5b3d761fb99_l3.png)
En bref, le résultat de la potentialisation est :
![]()
Comme vous l’avez vu dans cet exercice, la formule de la somme au carré est également utile pour calculer les puissances de grands nombres sans utiliser de calculatrice.
Carré d’une somme de 3 termes
Parfois, nous pouvons trouver que nous devons résoudre le carré de trois termes ajoutés, c’est-à-dire (a+b+c) 2 . Logiquement, dans ces cas, nous ne pouvons pas utiliser la formule que nous avons expliquée, car à l’intérieur des parenthèses, nous avons un trinôme au lieu d’un binôme. Il faut donc utiliser une formule différente.
La formule du carré de la somme de 3 termes est la suivante :
![]()
Voyons comment cette formule est appliquée à travers un exemple :
![Rendered by QuickLaTeX.com \begin{aligned} (2x+3y+5)^2 & = (2x)^2 + 2\cdot 2x (3y+5)+(3y)^2+2\cdot 3y \cdot 5 + 5^2 \\[2ex] & =4x^2 +4x (3y+5)+9y^2+30y +25 \\[2ex] &=4x^2 +12xy+20x+9y^2+30y +25 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-d0816bbe156553fc1ef5920ac2b2e09f_l3.png)
Comme vous pouvez le constater, l’ajout d’un élément à la formule rend le résultat beaucoup plus compliqué.