Calculer le plus petit commun multiple (lcm)

Le plus petit commun multiple (LCM) de deux nombres ou plus est le plus petit multiple (non nul) que ces nombres ont en commun. C’est l’opération inverse du plus grand commun diviseur , bien qu’elle soit calculée au moyen de méthodes similaires. Si vous souhaitez apprendre à calculer le LCM, nous vous recommandons de continuer à lire, car dans cet article nous vous expliquerons toutes les procédures (de la plus simple à la plus compliquée) pour trouver le plus petit commun multiple d’un ensemble de nombres.

calculatrice lcm

Avant de commencer à parler de la façon d’obtenir le lcm, nous voulons que vous sachiez que sur cette page, nous avons un calculateur multiple le moins commun . Avec lui, vous pourrez calculer le lcm de tous les nombres que vous voulez, de cette façon vous pourrez comparer les résultats de vos exercices pour voir si vous les avez correctement résolus.

Pour utiliser la calculatrice multiple la moins courante, saisissez les nombres entiers séparés par une virgule :

calculer lcm

Comment calculer le plus petit multiple commun ?

Pour trouver le plus petit commun multiple de deux nombres ou plus, vous devez suivre l'une des trois méthodes que nous expliquerons ci-dessous. Ensuite, lorsque nous détaillerons chacune des procédures que vous pouvez choisir, nous vous dirons également quels sont leurs avantages et leurs inconvénients. De cette façon, vous saurez lequel choisir dans chaque situation pour résoudre facilement et rapidement le LCM en question.

Méthode 1 : Lister les multiples

La première méthode consiste à créer une liste des multiples des nombres que vous souhaitez calculer dans le LCM. Ensuite, vous devez trouver la plus petite valeur qui se répète dans toutes les listes , de cette façon vous aurez le plus petit commun multiple. Ensuite nous allons le voir avec un exemple : lcm (5, 6).

Méthode 2 : décomposition factorielle

Deuxièmement, nous pouvons choisir de factoriser les nombres. Plus précisément, cette méthode facilitera le calcul du pcm des grands nombres . Étant donné que suivre la méthode 1 lors de l'exécution du lcm de grands nombres peut être lent et fastidieux, simplement parce que nous devrons écrire de très longues listes de multiples. Cette seconde procédure peut être un peu plus compliquée à appréhender dans un premier temps, mais quand on comprend la mécanique elle possède de nombreux avantages par rapport à la précédente. Cela dit, voyons la procédure à suivre :

• Décomposition factorielle : la première étape sera de décomposer tous les nombres que nous allons inclure dans le LCM en facteurs premiers. Dans le cas où vous ne savez pas comment décomposer un nombre de manière factorielle , nous vous recommandons d'entrer ce dernier lien, vous y trouverez une explication de première classe sur la façon de simplifier les nombres rapidement et efficacement.
• Créer une seule expression mathématique : lorsque nous aurons tous les nombres exprimés en facteurs premiers, nous choisirons les nombres communs et non communs élevés au plus grand exposant. Ensuite, vous les écrivez en une seule expression mathématique et enfin vous résolvez les multiplications et/ou puissances nécessaires. Et vous aurez déjà la valeur numérique du lcm.

Méthode 3 : Formule mathématique

Il existe un dernier moyen d'obtenir le plus petit commun multiple, qui consiste à utiliser le PGCD et la formule mathématique suivante :

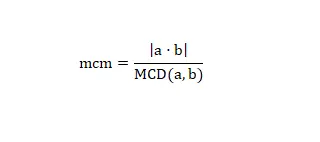
En utilisant cette formule, nous pouvons calculer le lcm de n'importe quel nombre. Voyons un exemple réel, si nous voulons calculer le lcm (2.6) nous devons simplement résoudre l'opération (2 x 6) / 2 = 6. Et nous aurons déjà résolu le calcul, comme vous pouvez le voir c'est une méthode simple et rapide si vous avez le GCD ou pouvez facilement le calculer.

Astuces pour calculer le lcm rapidement

Lorsque vous maîtriserez les trois méthodes que nous venons d'expliquer, nous vous recommandons de lire les propriétés du plus petit commun multiple dont nous allons parler maintenant. Puisque grâce à eux, vous pourrez identifier certaines situations spécifiques dans lesquelles le LCM peut être calculé très rapidement, sans avoir à utiliser les stratégies déjà expliquées.

• Premier nombre divisible par le second : si on veut calculer le plus petit commun multiple de a et b quand a divise b, alors le ppcm de ces deux nombres sera le plus grand (dans ce cas b). Par exemple, si vous voulez calculer le lcm de 2 et 8, le résultat sera le plus grand, donc 8.
• Deux nombres premiers : dans le cas de la recherche de deux nombres premiers , la méthode la plus rapide est de les multiplier ensemble et le résultat sera le ppcm. C'est logique, puisque son plus grand diviseur commun est 1, ce qui signifie que nous ne pourrons pas décomposer le nombre en facteurs plus simples que le nombre lui-même et, par conséquent, nous ne pourrons que les multiplier entre eux. Par exemple, le LCM de 3 et 5 sera le résultat de leur produit : 3 x 5 = 15.

Comment obtenir le plus petit commun multiple en fractions ?

Lorsque nous voulons résoudre une addition ou une soustraction de fractions, nous devons calculer le plus petit dénominateur commun, qui est le même que le lcm, mais appliqué aux fractions. Fondamentalement, nous recherchons le ppcm des deux dénominateurs afin de pouvoir ensuite exprimer la somme en une seule fraction. Si vous voulez voir comment le plus petit dénominateur commun est appliqué à un calcul de fraction réelle, vous pouvez entrer ce lien .

Lcm sur calculatrice scientifique

La clé LCM, que l'on trouve sur n'importe quelle calculatrice scientifique, permet de calculer le plus petit commun multiple de deux entiers. Dans le cas des calculatrices Casio, la syntaxe ou la procédure que vous devez suivre est la suivante. Tout d'abord, vous appuyez sur APHA + MCM (cette dernière touche sera étiquetée marron). Une fois cela fait, vous pouvez entrer les deux nombres, mais rappelez-vous que vous devez les séparer par une virgule ( SHIFT + , ). Enfin, vous obtiendrez le plus petit commun multiple en cliquant sur le bouton égal.

Exercices LCM résolus étape par étape

Ensuite, nous allons vous montrer trois exemples du multiple le moins commun résolu étape par étape . De cette façon, vous pouvez essayer de résoudre ces problèmes et pratiquer un peu ce que nous avons expliqué dans cet article. Il est important que vous essayiez de résoudre les exercices si vous voulez intérioriser les concepts, car il est nécessaire d'appliquer la théorie à la réalité. Cela dit, on vous laisse pratiquer avec les exercices :

Calculer le lcm de 4 et 6

Calculer le lcm de 6 et 9

Calculer le lcm de 30 et 40