Le binôme de Newton est une formule mathématique utilisée pour exprimer la somme de deux termes élevée à une puissance donnée . Cette formule, du nom du mathématicien britannique Isaac Newton, est utilisée dans de nombreux domaines des mathématiques.
Par exemple, il a une utilité dans les statistiques, la théorie des probabilités et le calcul différentiel et intégral. Le théorème du binôme nous permet de calculer la puissance d’un binôme de manière simple.
En termes simples, le binôme de Newton est basé sur une formule avec laquelle toute expression algébrique de la forme (a+b) n peut être résolue. Malgré le fait que cette formule porte le nom d’Isaac Newton, il convient de mentionner qu’il existe une controverse sur son origine.
C’est-à-dire que certaines recherches suggèrent de trouver l’utilisation du théorème binomial au Moyen-Orient.
Quand le binôme de Newton a-t-il été développé ?
Le théorème binomial de Newton, également connu sous le nom de binôme de Newton, a été développé en 1665 et communiqué pour la première fois dans deux lettres de l’officier de la Royal Society en 1676 .
Ces lettres étaient une réponse au mathématicien allemand Gottfried Wilhelm von Leibniz, qui cherchait à mieux comprendre les recherches mathématiques sur les séries infinies. Newton a partagé les résultats de son théorème et Leibniz a reconnu que c’était une technique utile pour obtenir des résultats en quadratures ou en séries.
Cette constatation a permis à Newton de conclure qu’il était possible d’opérer sur des séries infinies de la même manière que sur des expressions polynomiales finies . Bien que Newton n’ait jamais publié son théorème, le mathématicien britannique John Wallis l’a publié dans son algèbre en 1685 et a attribué sa création à Newton.
Pourquoi l’appelle-t-on binôme de Newton ?
Le binôme de Newton porte le nom du mathématicien et physicien anglais Isaac Newton, qui l’a développé au 17ème siècle . Newton n’a pas été le premier à découvrir ce théorème, mais il a été le premier à prouver sa validité pour tout entier positif n.
Le binôme de Newton est un outil mathématique très utile en algèbre et en calcul, et est largement utilisé dans des domaines tels que la physique, les statistiques, l’ingénierie et l’informatique.
Quelle est la formule du binôme de Newton ?
Comme nous l’avons mentionné précédemment, le binôme de Newton est la formule par laquelle les puissances d’un binôme peuvent être trouvées . Afin de trouver ladite puissance binomiale, les “coefficients binomiaux” sont utilisés. Le terme précédent fait référence aux séquences de combinaisons.
Dans cet esprit, nous pouvons décomposer les formules binomiales de Newton comme suit :
- (une + b) 2 = une 2 + 2ab + b 2
- (a – b) 2 = a 2 – 2ab + b 2
- (une + b) 3 = une 3 + 3a 2 b + 3 ab 2 + b 3
Les expressions mathématiques qui font référence au développement de (a+b) n sont dites entités notables, et permettent d’obtenir une formule générale qui représente cette opération pour tout entier naturel « n ».
En examinant les coefficients de chaque polynôme résultant, on peut remarquer une séquence qui suit ce que l’on appelle le Triangle de Pascal .
La séquence du triangle de Pascal commence par le chiffre 1, et dans chaque ligne suivante, les chiffres finaux sont toujours 1. Les valeurs intermédiaires sont obtenues en additionnant les deux nombres de la ligne précédente qui sont directement au-dessus de la valeur à calculer.
Comment trouver un terme dans le binôme de Newton ?
Pour trouver un terme spécifique dans le binôme de Newton, la formule générale est utilisée :
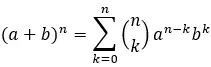
Où:
a et b sont les coefficients du binôme.
n est l’exposant du binôme.
k est le terme spécifique que nous voulons trouver.
Σ représente la somme de k=0 à n.
[nk] est le coefficient binomial calculé par la formule suivante :
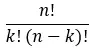
Par conséquent, la formule entièrement développée est telle que :
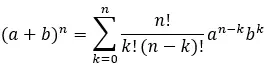
Exemple de binôme de Newton résolu
Une fois ces valeurs trouvées, elles sont substituées dans la formule et l’expression est résolue pour obtenir le terme spécifique. Par exemple, si nous voulons trouver le cinquième terme du binôme (2x + 3) 6 , nous aurions :
un = 2x
b = 3
n = 6
k = 5
Ainsi, en utilisant la formule :
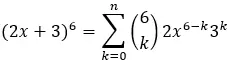
Le cinquième terme correspond à k=5, on a donc :
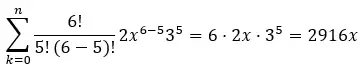
Par conséquent, le cinquième terme du binôme (2x + 3) 6 est 2916x.
Qu’est-ce qu’un binôme de Newton de degré 5 ?
Un binôme de Newton de degré 5 est une expression algébrique de la forme (a + b) 5 , où « a » et « b » sont des variables et l’ exposant 5 indique le degré du binôme . En développant cette expression, nous obtenons un polynôme quadratique qui a six termes :
(une + b) 5 = une 5 + 5a 4 b + 10a 3 b 2 + 10a 2 b 3 + 5ab 4 + b 5
Chaque terme de ce polynôme est obtenu en combinant les coefficients du binôme avec les puissances de « a » et « b ». Par exemple, le second terme (5a 4 b) s’obtient en multipliant le coefficient binomial (5 choisissent 1 = 5) par « a » élevé à la puissance quatre et par b élevé à la première puissance.
Les binômes de Newton de degré 5 sont utiles dans différentes branches des mathématiques et de la physique, telles que les statistiques, la théorie des probabilités et la mécanique quantique.
Quelles sont les applications du binôme de Newton ?
Le binôme de Newton a une grande variété d’applications dans divers domaines, notamment :
- Calcul des probabilités : Le théorème binomial est utilisé pour calculer les probabilités d’événements binomiaux, tels que le tirage au sort ou le succès ou l’échec d’une série de tests.
- Théorie des nombres – Le binôme de Newton est utilisé pour développer les polynômes et simplifier les équations en théorie des nombres.
- Statistiques : Le binôme de Newton est utilisé pour calculer des distributions binomiales et dans la construction d’intervalles de confiance.
- Physique – En physique, le théorème binomial est utilisé dans la théorie de la relativité et en mécanique quantique, entre autres domaines.
- Économie et finance : Le binôme de Newton est utilisé pour calculer la valeur actuelle et future des flux de trésorerie dans le temps et dans la valorisation des options financières.
- Programmation et informatique : Le binôme de Newton est utilisé dans le développement d’algorithmes et dans la programmation informatique.
Pourquoi le binôme de Newton est-il important ?
Le binôme de Newton est pertinent car c’est un outil mathématique fondamental pour le développement de l’algèbre et de la théorie des nombres . Il permet de calculer le résultat de l’élévation au carré ou à toute autre puissance d’un binôme, ce qui est très utile pour résoudre des équations et simplifier des expressions algébriques.
En outre, il a des applications dans des domaines tels que les statistiques, les probabilités et la physique , entre autres. En résumé, le binôme de Newton est un concept essentiel en mathématiques et sa compréhension est cruciale pour progresser dans de nombreux domaines d’études.
Existe-t-il d’autres façons d’exprimer le binôme de Newton ?
Oui, il existe d’autres façons d’exprimer le binôme de Newton. Par exemple, il peut être exprimé en termes de coefficients binomiaux en utilisant la notation combinatoire.
En outre, il peut être exprimé en termes de fonctions exponentielles et de fonctions trigonométriques à l’aide de la formule d’Euler. De même, en termes de fonction gamma en utilisant la formule de Legendre. Ces expressions alternatives peuvent être utiles dans différents contextes et problèmes mathématiques.
Exemples de binôme de Newton
Voyons ensuite quelques exemples simples d’application du binôme de Newton.
Exemple 1 : Calculer le terme d’ordre 3 dans le développement de (x + y) 5 .
Solution : Dans le développement de (x + y) 5 , le coefficient du premier terme est 1, le coefficient du deuxième terme est 5, le coefficient du troisième terme est 10, le coefficient du quatrième terme est 10, le coefficient du cinquième terme est 5 et le coefficient du sixième terme est 1.
Le terme d’ordre 3 est donc :
10x 2 et 3
Exemple 2 : Trouver le terme indépendant dans le développement de (2x – 1) 4 .
Solution : Dans le développement de (2x – 1) 4 , le terme indépendant se trouve dans la combinaison (2x) p (-1) (4-p) , où p est la valeur qui fait que l’exposant de (2x) p et (-1) (4-p) totalisent 4.
Le terme indépendant est donc :
(2x) 2 (-1) 2 = 4
Exemple 3 : Trouver le terme de degré le plus élevé dans le développement de (3x – 2y) 6 .
Solution : Le terme de degré le plus élevé dans le développement de (3x – 2y) 6 se trouve dans la combinaison (3x) p (-2y) (6-p) , où p est la valeur qui rend l’exposant de (3x) p et (-2y) (6-p) égal au degré du binôme, qui est 6.
Par conséquent, le terme du degré le plus élevé est:
(3x) 3 (-2y) 3 = -216x 3 et 3