Les nombres complexes sont un ensemble composé de nombres réels et de nombres imaginaires . Ces deux derniers ensembles numériques peuvent être représentés graphiquement au moyen de la droite réelle et de la droite imaginaire. Et lorsque nous plaçons les deux lignes dans le même plan, le plan complexe bien connu est formé.
Qu’est-ce que le plan complexe ?
Le plan complexe est formé par l’axe réel (axe X), qui équivaut à la ligne réelle et, d’autre part, l’axe imaginaire (axe Y), qui conceptualise la ligne imaginaire.
Il convient de noter que ce plan comprend tous les nombres complexes. Par conséquent, peu importe sa taille ou sa taille, ou la forme sous laquelle un nombre complexe est écrit, il peut être représenté graphiquement sur le plan. Voyons donc comment ces nombres sont représentés dans le plan complexe.
Comment représenter graphiquement des nombres complexes sur le plan complexe ?
Comme nous le savons déjà (ou si vous ne le savez pas, nous vous conseillons de lire notre article sur les nombres complexes ), il existe trois manières d’écrire un complexe : la forme binomiale, la forme polaire et la forme trigonométrique. Chacun exprime la valeur complexe suivant une structure différente, donc la méthode à suivre pour faire les représentations graphiques est différente.
Ensuite, nous expliquons la marche à suivre dans les trois cas :
Représentation sous forme binomiale
Lorsqu’on a un nombre complexe en notation binomiale , qui est la plus courante, il faut regarder la structure du nombre :

où a est la partie réelle et b est la partie imaginaire.
Sachant cela, on en déduit que la valeur de a est celle que l’on utilise pour l’abscisse (axe réel) et la valeur de b est celle que l’on utilise pour l’ordonnée (axe imaginaire). Avec l’exemple suivant, vous le comprendrez mieux.
Nous allons essayer de représenter le nombre : 3 + 2i.
La première chose est de dessiner le graphique (en signalant que l’axe horizontal est le vrai et l’axe vertical est l’imaginaire):

Ensuite, on localise le point du graphe en coordonnées cartésiennes (x, y), que l’on a déduites du nombre complexe. Dans cet exemple pratique, notre point est (3, 2).
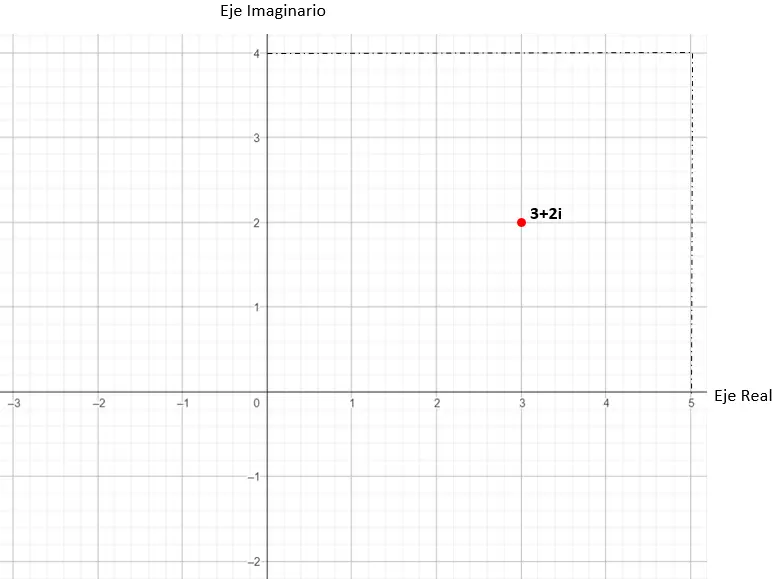
Ainsi la valeur 3 + 2i serait représentée dans le plan complexe.
Représentation sous forme polaire
Nous allons maintenant voir comment un nombre complexe est représenté sous forme polaire . Pour bien comprendre cette méthode, il faut savoir que la notation polaire définit un nombre complexe à partir du module et de l’argument. Qui sont utilisées dans la représentation graphique comme coordonnées polaires (et non comme coordonnées cartésiennes !).
Et la caractéristique principale du système de coordonnées polaires est que l’emplacement d’un point est décrit au moyen d’un vecteur et d’un angle (pas comme la méthode précédente). Qui correspondent au module et à l’argument des nombres complexes. Ensuite, nous vous montrons la formule universelle de la forme polaire d’un nombre complexe :

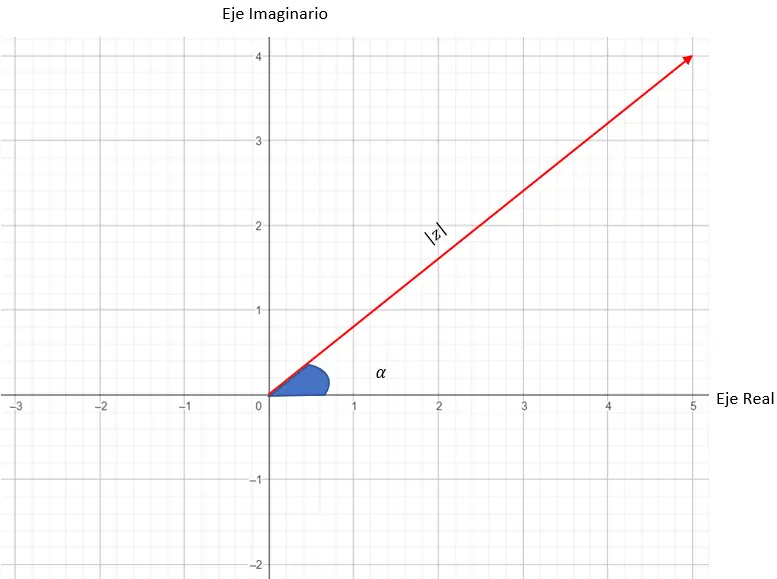
Où |z| est le module et α est l’argument. Ces deux variables se traduisent dans le plan par :
- Module : c’est la longueur qui définit un vecteur (entre l’origine et le point équivalent à notre nombre).
- Argument : est l’angle que fait le vecteur avec l’axe X.
Par conséquent, le module d’un nombre complexe correspond à la longueur du vecteur que nous utilisons pour faire la représentation graphique. Alors que l’argument ou l’angle du nombre complexe correspond à l’angle entre le vecteur et l’axe X. Ci-dessous, vous pouvez voir un schéma qui place toutes les variables :
Maintenant, nous allons essayer de représenter le nombre : 3 45 .
Premièrement, nous devons identifier le module et l’argument :
- Module : 3.
- Argument : 45 degrés.
Ensuite, nous devons trouver les points sur le graphique qui ont un module égal à 3, dans ce cas, tout point sur un cercle de rayon 3 fonctionnera.
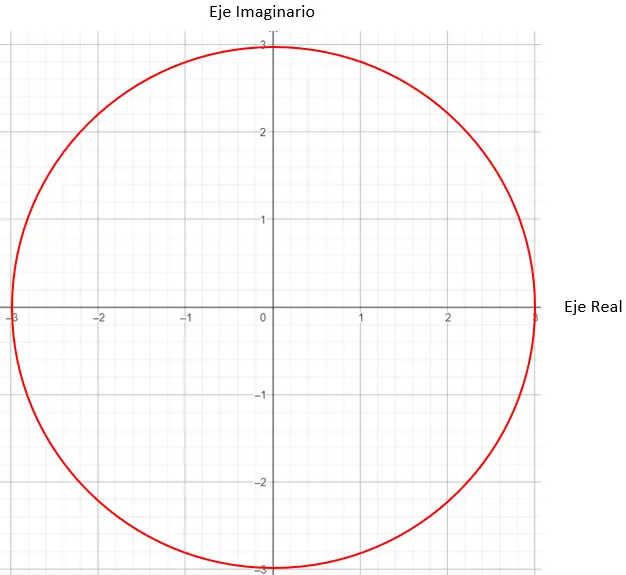
Et pour finir de déterminer quel est le point exact, nous devons mettre la condition que le vecteur généré par le module et l’origine doivent faire un angle de 45 degrés avec l’axe X.
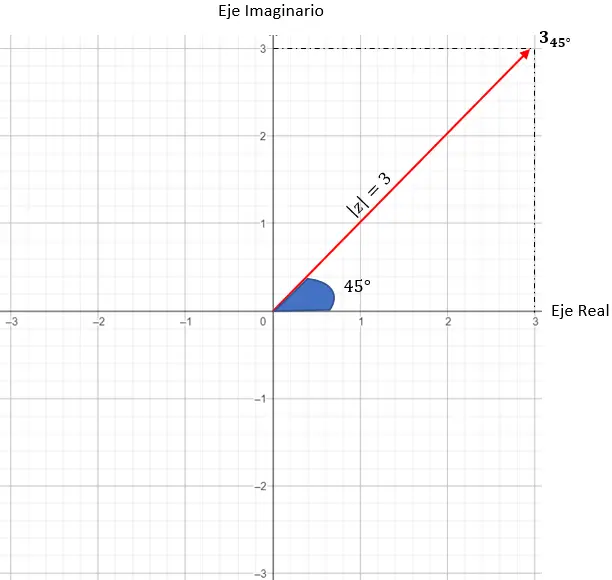
Et nous avons déjà un nombre complexe représenté en notation polaire.
Représentation sous forme trigonométrique
Enfin, il nous reste à expliquer comment un nombre complexe est représenté sous forme trigonométrique . Ce cas et le précédent sont pratiquement les mêmes, car la forme polaire et la forme trigonométrique utilisent les mêmes données pour exprimer un nombre complexe : le module et l’argument. Cela ne change que la structure de l’expression :

Où, |z| est le module et α est l’argument.
Il faut donc profiter de la même méthode que dans le cas précédent : utiliser le module comme “longueur” et l’argument comme angle. En voyant l’exemple suivant, vous le comprendrez mieux.
Nous allons représenter z = 4 · (cos (45) + i · sin(45)).
La première chose est d’identifier le module et l’angle :
- Module : 4.
- Argument : 45 degrés.
Ensuite, il faut trouver les points sur le graphe qui ont un module égal à 4, dans ce cas n’importe quel point sur un cercle de rayon 4 fonctionnera.
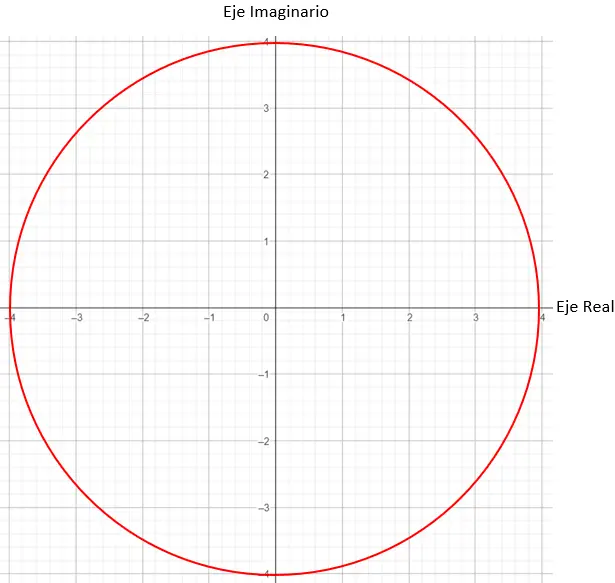
Et enfin, nous localisons le point exact, exigeant que l’angle formé entre le vecteur module et l’axe X soit de 45 degrés, comme l’argument nous l’indique.
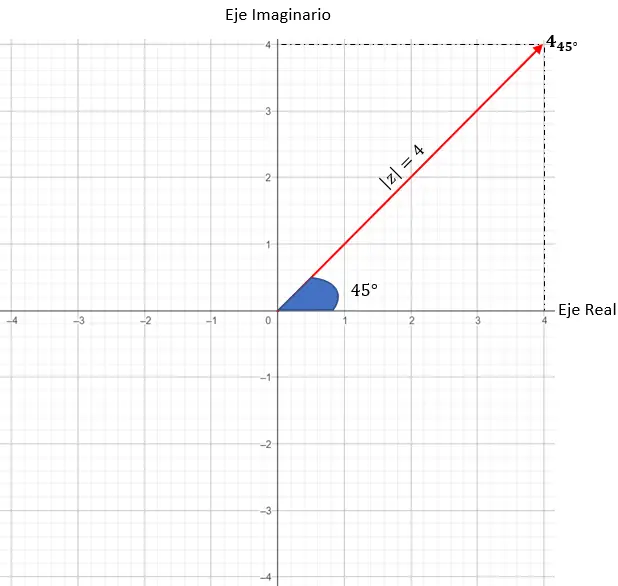
Et donc nous représentons un nombre complexe sous forme trigonométrique.
Exercice d’avion complexe
Pour terminer cette publication, nous allons proposer un dernier exercice. Nous vous recommandons vivement de le résoudre, car vous consoliderez ainsi les connaissances expliquées tout au long de cet article.
Preuve de la représentation graphique des trois nombres complexes suivants sur le plan complexe :
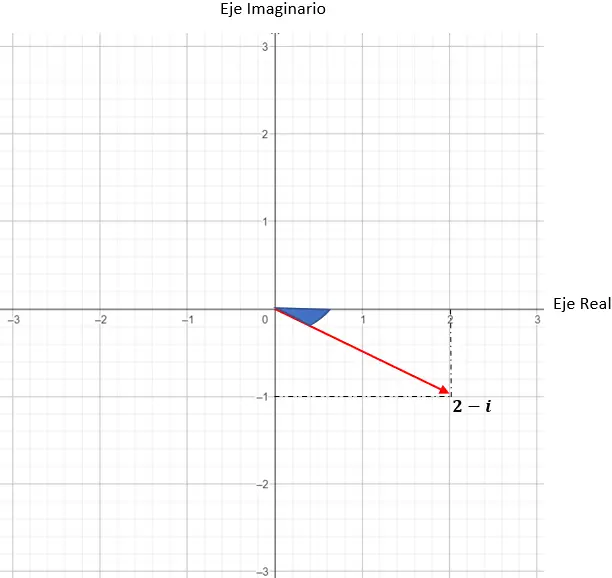
z = 2 – je
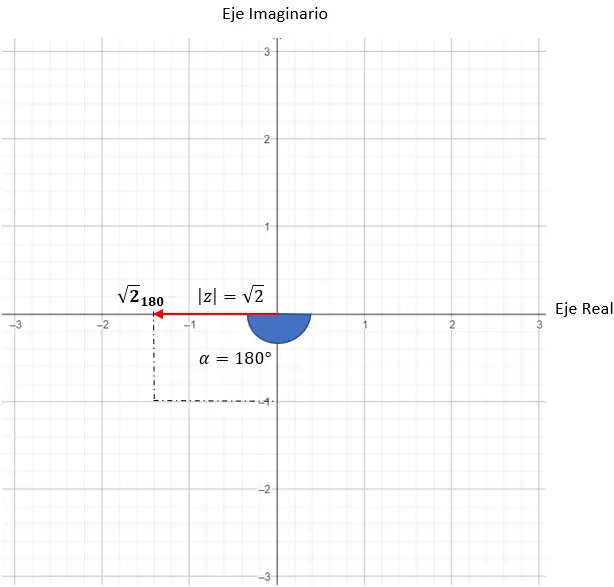
w = √2180
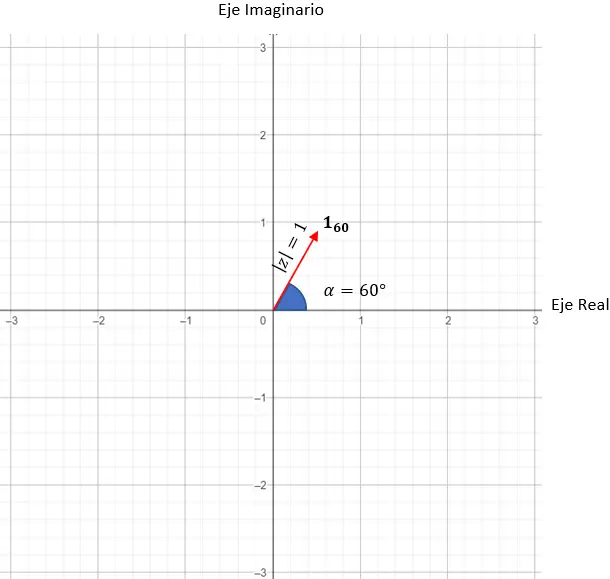
p = cos(60) + je sin(60)