دالة خطية ووظيفة تقاربية -

ستجد في هذه المقالة شرح الدالة الأفينية والدالة الخطية، بالإضافة إلى الاختلافات الموجودة بين هذين النوعين من الدوال. بالإضافة إلى ذلك، سترى أمثلة على كيفية رسم دالة تقاربية ودالة خطية وكيفية حساب تعبيراتهما من نقطتين. وأخيرا، سوف تكون قادرا على التدرب مع العديد من التمارين التي تم حلها خطوة بخطوة.

ما هي وظيفة أفينية وظيفة خطية؟

تعريفات الدالة المتقاربة والدالة الخطية هي كما يلي:

الدالة المتقاربة هي دالة متعددة الحدود من الدرجة الأولى، أي دالة تمثل خطًا مستقيمًا، ممثلة في الرسم البياني. الوظائف المرتبطة هي كما يلي:

$f(x)=mx+n$

ذهب

$m$

هو ميل الخط و

$n$

هذا هو التقاطع y، حيث تتقاطع الدالة مع المحور الرأسي.

في الرياضيات، تُسمى الدوال المتقاربة أيضًا بالتحويلات الخطية في سياق الجبر الخطي.

الدالة الخطية هي دالة تقاربية لا تحتوي على مصطلح مستقل. ولذلك، فإن صيغة الوظائف الخطية هي:

$f(x)=mx$

ذهب

$m$

هو ميل الخط.

المجال والمدى (أو المدى) للدالة الخطية والدالة المتقاربة كلها أرقام حقيقية:

$\text{Dom } f=\mathbff{R}$

$\text{Im } f= \mathbb{R}$

ما هو الفرق بين وظيفة خطية ووظيفة أفينية؟

الآن بعد أن رأيت مفهومي الوظيفة الخطية والوظيفة التقريبية، ستلاحظ أنهما متشابهان جدًا مع بعضهما البعض. ومع ذلك، فإن الفرق التالي بينهما مهم جدا:

الفرق الوحيد بين الدالة الخطية والدالة المتقاربة هو أن الدالة الخطية لا تحتوي على مصطلح مستقل بينما الدالة المتقاربة دائمًا يكون معامل التقاطع (n) مختلفًا عن الصفر (0).

دالة خطية

$f(x)=mx$

دالة خطية

$f(x)=mx+n$

وهذا يعني أن الدالة الخطية تمر دائمًا عبر أصل الإحداثيات ، النقطة (0,0). من ناحية أخرى، لن تمر الدالة التقاربية أبدًا عبر هذه النقطة لأنها تحتوي على تقاطع غير 0.

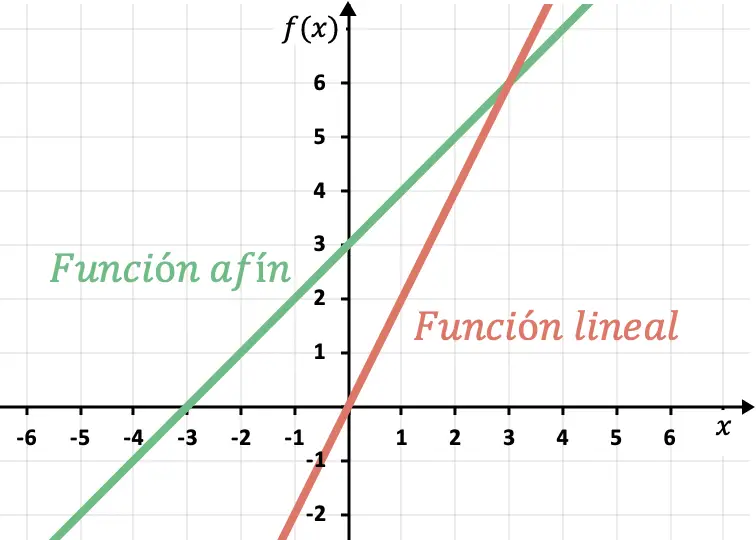
ما هو الفرق بين وظيفة خطية ووظيفة أفينية؟

الميل والتقاطع y للدالة الخطية أو المتقاربة

في هذا القسم، سنقوم بتحليل مثال على دالة أفينية أو خطية لفهم معنى المصطلحات

$m$

$n$

، أو بمعنى آخر، الميل وتقاطع y.

حدد تعبير الدالة الموضحة في الرسم البياني وصنفها كدالة خطية أو تقاربية.

تتبع هذه الأنواع من الوظائف التعبير التالي:

$f(x)=mx+n$

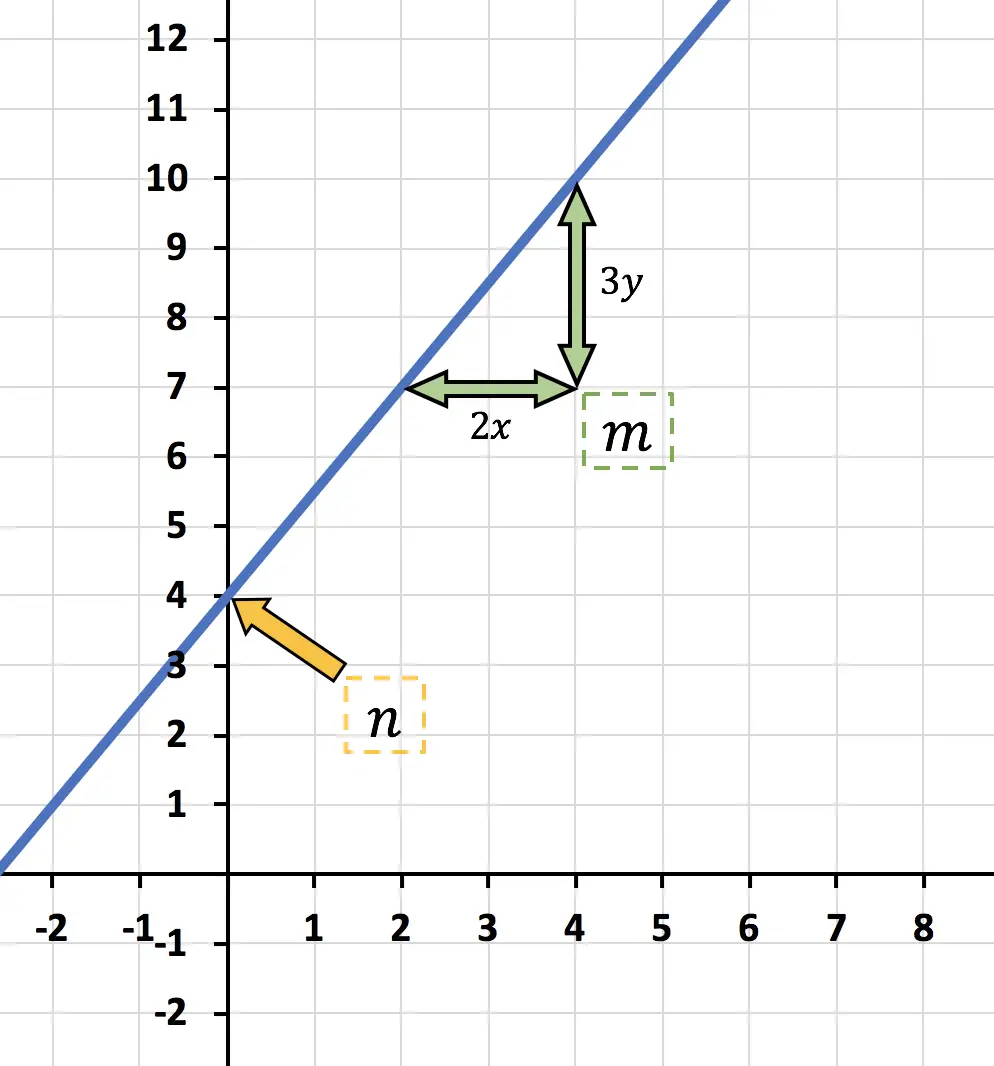
بمعنى الميل والتقاطع y الخطي أو الدالة المتقاربة m و n

$n$

هذا هو التقاطع y، أي حيث تتقاطع الدالة مع المحور Y الرأسي. لذلك في هذه الحالة:

$n=4$

وعلى جانب آخر،

$m$

هو ميل الخط. يمكن حساب Y بقسمة الفرق في y بين نقطتين على الفرق في x بين نفس النقطتين:

$m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}$

$m$

يقول “كم يزيد y لكل x” ، لذلك في هذه الحالة الدالة “3y تزيد لكل 2x” .

في الختام، التعبير عن الدالة التقاربية الممثلة في الرسم البياني هو:

$\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}$

بالإضافة إلى ذلك، نظرًا لأن تقاطع y ليس صفرًا، فهو دالة تقاربية .

نعرض لك أدناه المزيد من الأمثلة على الوظائف الخطية والمتقاربة لإكمال فهمك:

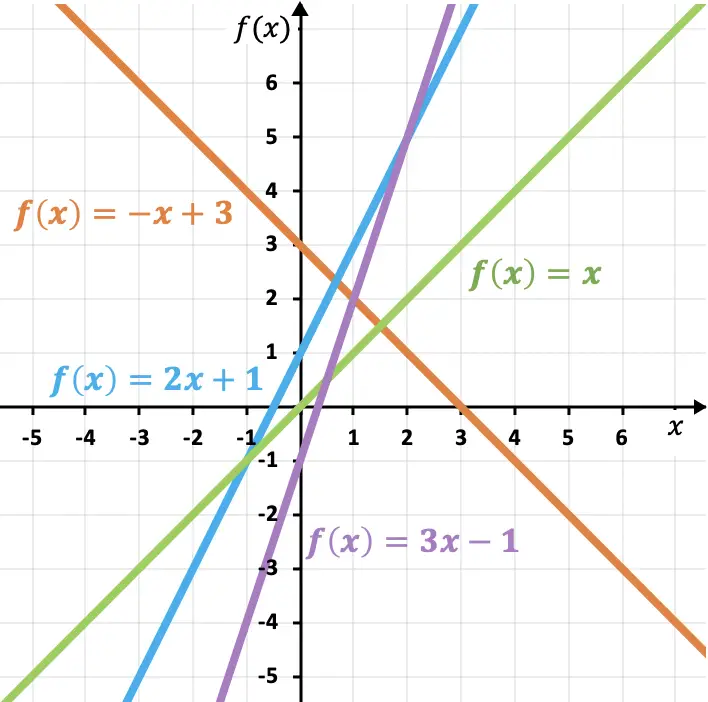
كما ترون في هذه الأمثلة، كلما زاد الميل، كلما كان الخط أكثر انحدارًا، وبالتالي زادت الدالة. وبالمثل، يحدد معامل الميل نمو أو نقصان الدالة:

إذا كان الميل موجبًا، فإن الدالة تتزايد ، أي أنها تزيد مع زيادة x .
إذا كان الميل سالبًا، فإن الدالة تتناقص ، أي أنها تتناقص مع زيادة x .

بالإضافة إلى ذلك، يمكنك أيضًا معرفة ما إذا كان الخطان متوازيين أو متعامدين من خلال ميليهما:

عندما يكون لخطين نفس الميل، فإنهما يكونان متوازيين ، أي لا يتقاطعان في أي نقطة أو يكونان متطابقين تمامًا.

$m_1 = m_2$

من ناحية أخرى، الخطان متعامدان ، أي أنهما يتقاطعان بزاوية رأسية (90 درجة)، إذا كان ميلاهما يتوافقان مع العلاقة التالية:

$m_1 = -\cfrac{1}{m_2}$

مثال لتمثيل دالة تقاربية أو خطية

دعونا نرى كيفية رسم دالة من الدرجة الأولى باستخدام مثال.

قم برسم دالة affine التالية:

$f(x)=2x-1$

أول شيء يتعين علينا القيام به هو إنشاء مجموعة من القيم. للقيام بذلك، نمنح القيم التي نريدها

$x$

للحصول على قيم

$f(x)$

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

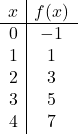
على الرغم من أن جدول القيم بنقطتين يكفي، إلا أنه يمكننا عمل المزيد من النقاط للتأكد من صحته.

بمجرد إنشاء جدول القيم، نرسم النقاط على الرسم البياني:

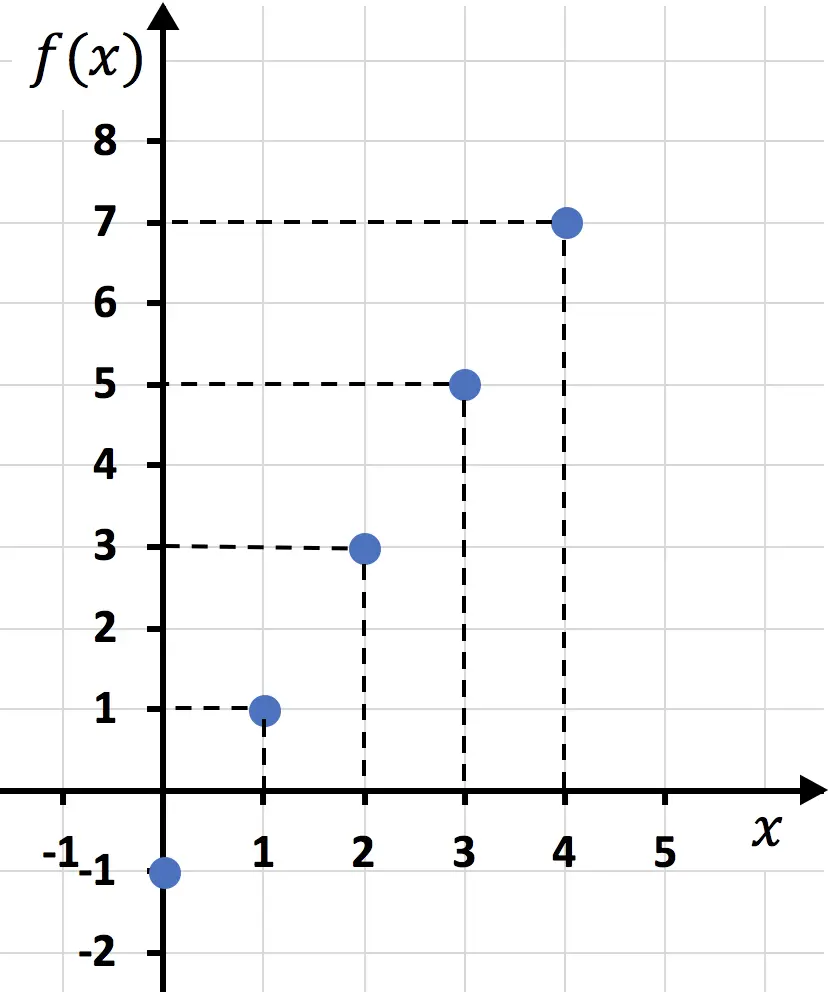
وأخيرًا نجمع النقاط ونرسم خطًا:

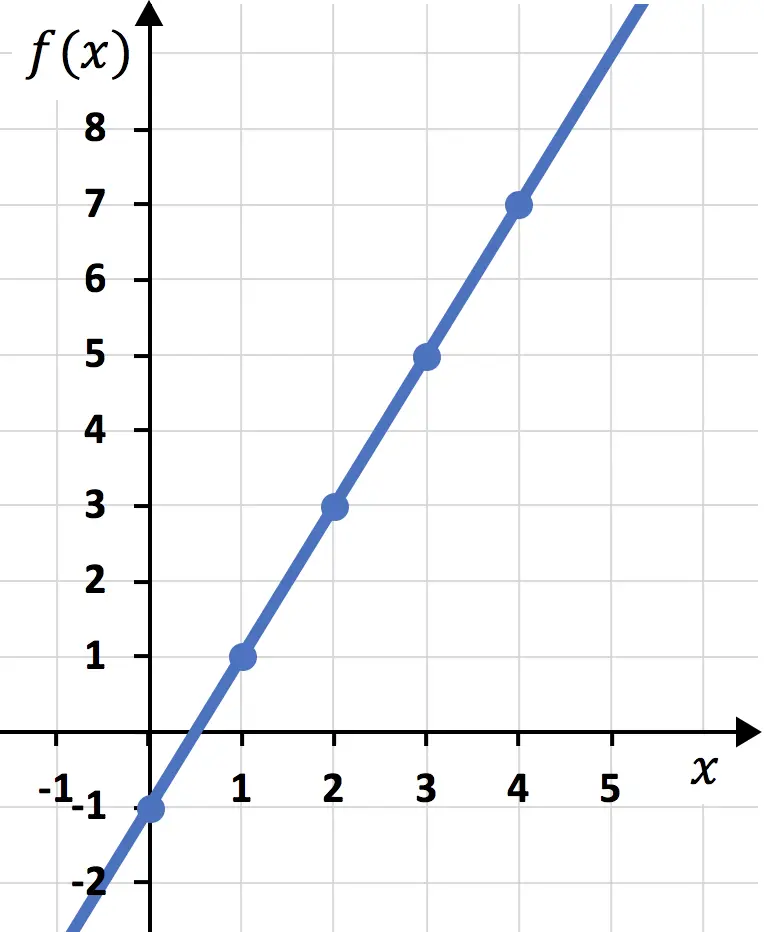
وبهذه الطريقة، نكون قد مثلنا الدالة بالفعل على الرسم البياني. كما ترون، الأمر ليس معقدًا، ما عليك سوى إنشاء جدول قيم أولاً ثم رسم النقاط على الرسم البياني.

كيفية حساب دالة خطية أو متقاربة من نقطتين

الآن دعونا نرى كيفية العثور على دالة خطية أو متقاربة من نقطتين باستخدام مثال:

احسب الدالة الخطية التي تحققها
$f(3)=5$

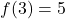
وانتقل من خلال هذه النقطة

$(1,-1).$

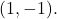
أولاً،

$f(3)=5$

وهذا يعني أن الدالة تمر عبر النقطة

$(3,5)$

ومن ثم، بما أن لدينا نقطتين تمر عبرهما الدالة، فيمكننا حساب الميل

$m$

وظيفة:

وبالنظر إلى نقطتين،

$P_1=(x_1,y_1)$

$P_2=(x_2,y_2)$

، ميل

$m$

يتم حساب الدالة:

$m=\cfrac{y_2-y_1}{x_2-x_1}$

في حالتنا تمر الدالة عبر النقاط

$(3,5)$

$(1,-1)$

. لذلك المنحدر

$m$

من الدالة هي:

$m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3$

وبالتالي ستكون الدالة على الشكل:

$f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n$

بمجرد أن نعرف

$m$

يمكننا حل اللغز

$n$

. للقيام بذلك، نعوض بإحداثيات نقطة تنتمي إلى الدالة في المعادلة. على سبيل المثال النقطة (3.5):

$f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n$

نحل المعادلة الناتجة:

$5=3\cdot 3+n$

$5= 9 + n$

$5-9=n$

$-4=n$

وبالتالي فإن الدالة الخطية هي:

$\bm{f(x)=3x-4}$

تمارين محلولة على الدوال الخطية والأفينية

التمرين 1

حدد ميل وأصل الدالة التقريبية التالية:

$f(x)=-5x-2$

انظر الحل

الدالة الخطية لها الشكل

$f(x)=mx+n .$

وبالتالي فإن ميل الدالة هو الرقم المصاحب لـ x ، وهو في هذه الحالة -5:

$\bm{m=-5}$

والتقاطع y هو الحد المستقل، وهو في هذه الحالة -2:

$\bm{n=-2}$

تمرين 2

قم برسم دالة affine التالية:

$f(x)=x+1$

انظر الحل

نعطي القيم أولاً

$x$

لإنشاء جدول القيم:

$x= 0 \ \longrightarrow \ f(0)=0+1 = 1$

$x= 1 \ \longrightarrow \ f(1)=1+1= 2$

$x= 2 \ \longrightarrow \ f(2)=2+1 = 3$

$x= 3 \ \longrightarrow \ f(3)=3+1 = 4$

$x= 4 \ \longrightarrow \ f(4)=4+1 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}$

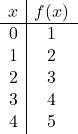
ثم نمثل النقاط من جدول القيم على الرسم البياني ونرسم الخط:

التمرين 3

ارسم الدالة التالية على الرسم البياني:

$f(x)=-2x+6$

انظر الحل

نعطي القيم أولاً

$x$

لإنشاء جدول القيم:

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6$

$x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4$

$x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2$

$x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0$

$x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}$

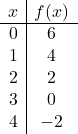
وأخيرًا نمثل النقاط من جدول القيم على الرسم البياني ونرسم الخط:

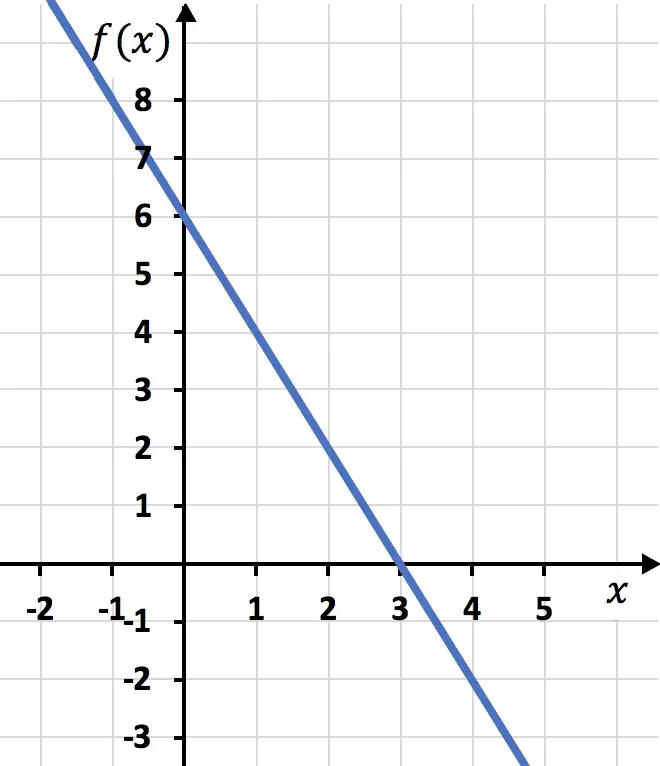
تمرين تم حله خطوة بخطوة للدالة الخطية والتقاربية

التمرين 4

أوجد التعبير الخاص بالدالة التقريبية التي تمر بالنقطتين (2،3) و (0،1).

انظر الحل

تمر الدالة بالنقطتين (2,3) و (0,1) فيكون ميل الدالة كما يلي:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1$

والدالة ستكون على الشكل:

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

بمجرد أن نعرف m، يمكننا حساب n . للقيام بذلك، علينا التعويض بإحداثيات نقطة تنتمي إلى الدالة في المعادلة. على سبيل المثال النقطة (2،3):

$f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}$

$3=2+n$

يجب علينا الآن حل المعادلة الناتجة:

$3-2=n$

$1 = n$

وبالتالي فإن الوظيفة تتوافق مع التعبير التالي:

$\bm{f(x)=x+1}$

التمرين 5

قم برسم دالة affine التالية:

$f(x)=2x-1$

انظر الحل

نعطي القيم أولاً

$x$

لإنشاء جدول القيم:

$x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

ثم نمثل النقاط من جدول القيم على الرسم البياني ونرسم الخط:

التمرين 6

احسب الدالة الخطية التي تحقق الشرطين التاليين:

$\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}$

انظر الحل

نرجو أن يتحقق

$f(3)=-2$

وهذا يعني أن الدالة تمر بالنقطة (3،-2). وبنفس الطريقة،

$f(-1)=6$

وهذا يعني أن الدالة تمر بالنقطة (-1.6).

إذن تمر الدالة بالنقطتين (3,-2) و (-1,6) فيكون ميلها:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2$

وبالتالي ستكون الدالة على الشكل:

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

وبمجرد أن نعرف m، يمكننا حساب n . للقيام بذلك، نعوض بإحداثيات النقطة التي تنتمي إلى الدالة في المعادلة. على سبيل المثال النقطة (3،-2):

$f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n$

ونحل المعادلة الناتجة:

$-2=-6+n$

$-2+6=n$

$4 = n$

وبالتالي فإن الوظيفة هي:

$\bm{f(x)=-2x+4}$

التمرين 7

ابحث عن الوظيفة التقاربية التي يؤديها

$f(1) =6$

ويمر بالنقطة (3.5).

انظر الحل

نرجو أن يتحقق

$f(1)=6$

وهذا يعني أن الدالة تمر بالنقطة (1،6).

وبالتالي فإن الدالة تمر بالنقطتين (1.6) و (3.5) وبالتالي يكون ميلها:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}$

وبالتالي ستكون الدالة على الشكل:

$\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n$

بمجرد أن نعرف المصطلح m يمكننا حساب المعامل n . للقيام بذلك، نعوض بإحداثيات النقطة التي تنتمي إلى الدالة في المعادلة. على سبيل المثال النقطة (1،6):

$\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n$

نحل المعادلة الناتجة:

$6=-\cfrac{1}{2}+n$

$6+\cfrac{1}{2}=n$

تذكر أنه لجمع الكسور، يجب عليك أولًا اختزالها إلى مقام مشترك ثم إضافة البسطين:

$\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n$

$\cfrac{12}{2} +\cfrac{1}{2}=n$

$\cfrac{13}{2}=n$

وبالتالي فإن الوظيفة هي:

$\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}$

التمرين 8

حل المشكلة التالية المتعلقة بالوظائف الخطية والتقاربية:

يبيع متجر 40 وحدة من المنتج عندما يكون السعر 15 يورو/وحدة، و65 وحدة عندما يكون السعر 10 يورو/وحدة.

احسب دالة الطلب للمنتج، على افتراض أنها دالة تقاربية.
كم عدد الوحدات التي سيتم بيعها إذا تم تحديد السعر بـ 12 يورو للوحدة؟

انظر الحل

وبما أنها دالة متقاربة، فإن الدالة ستكون من النوع

$f(x)=mx+n .$

ذهب

$x$

سيكون سعر الوحدة للمنتج و

$f(x)$

سوف تكون الوحدات المباعة.

يخبرنا البيان الصحفي أنه عندما يكون السعر 15 يورو للوحدة، يتم بيع 40 وحدة. لذلك، كما

$x$

هو الثمن و

$f(x)$

الوحدات المباعة، يجب احترام المساواة التالية:

$f(15)=40$

وعندما يكون السعر 10 يورو/وحدة، يتم بيع 65 وحدة. لذلك، باستخدام نفس المنطق:

$f(10)=65$

نرجو أن يتحقق

$f(15)=40$

وهذا يعني أن الدالة تمر بالنقطة (15.40). و

$f(10)=65$

وهذا يعني أن الدالة تمر بالنقطة (10.65).

وبالتالي فإن ميل الدالة هو:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5$

وبالتالي ستكون الدالة على الشكل:

$f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n$

بمجرد أن نعرف m، يمكننا حساب n . للقيام بذلك، نعوض بإحداثيات النقطة التي تنتمي إلى الدالة في المعادلة. على سبيل المثال النقطة (3:40 مساءً):

$f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n$

ونحل المعادلة الناتجة:

$40=-75+n$

$40+75=n$

$115 = n$

وبالتالي فإن الوظيفة التي تربط المبيعات التي تتم بالسعر هي:

$\bm{f(x)=-5x+115}$

ومن ناحية أخرى، في الوظيفة

$x$

يمثل السعر. لذلك، لمعرفة عدد الوحدات التي سيتم بيعها إذا كان السعر 12 يورو/وحدة، يجب علينا الحساب

$f(12):$

$f(x)=-5x+115 \ \xrightarrow{x \ = \ 12} \ f(12)=-5\cdot 12+115$

$f(12)=-60+115$

$f(12)=\bm{55}$

لذا، إذا كان السعر 12 يورو/وحدة ، فسيتم بيع 55 وحدة.

دالة خطية ووظيفة أفيني

ما هي وظيفة أفينية وظيفة خطية؟

ما هو الفرق بين وظيفة خطية ووظيفة أفينية؟

الميل والتقاطع y للدالة الخطية أو المتقاربة

مثال لتمثيل دالة تقاربية أو خطية

كيفية حساب دالة خطية أو متقاربة من نقطتين

تمارين محلولة على الدوال الخطية والأفينية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

التمرين 8

اترك تعليقاً إلغاء الرد