وظيفة ثابتة

يوليو 4, 2023

نوضح في هذه المقالة ما هي الدالة الثابتة وما هو تمثيلها الرسومي. بالإضافة إلى ذلك، ستتمكن من رؤية عدة أمثلة للوظائف الثابتة وجميع خصائص هذا النوع من الوظائف. وأخيرًا، ستتمكن من التدرب من خلال تمارين محلولة للدوال الثابتة.

ما هي الدالة الثابتة؟

الدالة الثابتة هي تلك الدالة التي تأخذ دائمًا نفس الصورة لأي قيمة للمتغير المستقل (x) ، أي أن الدالة الثابتة هي من الشكل f(x)=k حيث k هو أي رقم حقيقي.

$f(x)=k$

التمثيل الرسومي للدالة الثابتة هو خط أفقي.

على سبيل المثال، جميع الوظائف التالية هي ثوابت:

$f(x)=1 \qquad f(x)=7 \qquad f(x)=5$

تمثيل رسومي لوظيفة ثابتة

بعد أن تعرفنا على مفهوم الدالة الثابتة، سنرى كيفية تمثيل دالة ثابتة في الرسم البياني.

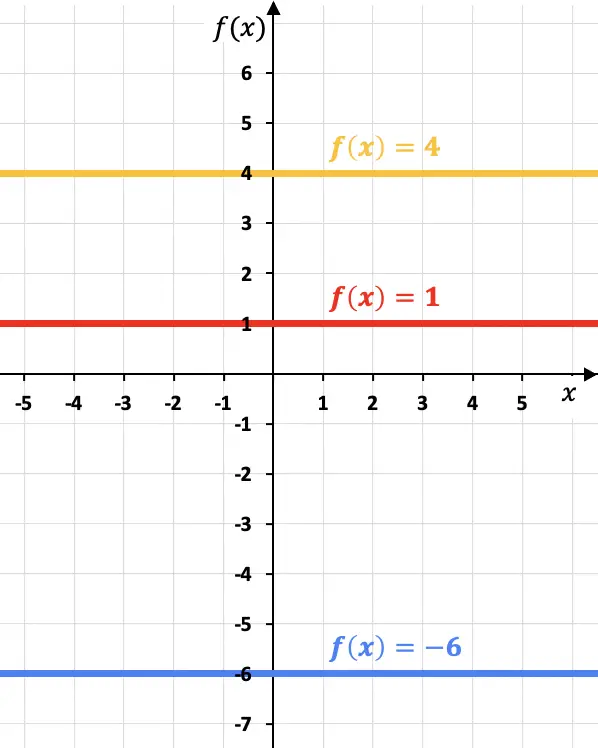
يعد رسم دالة ثابتة أمرًا بسيطًا للغاية، ما عليك سوى رسم خط أفقي في قيمة الدالة (k).

انظر إلى الأمثلة التالية التي قمنا فيها بتمثيل ثلاث دوال ثابتة مختلفة على الرسم البياني:

وظائف ثابتة

لاحظ أن كل دالة ثابتة موازية للمحور السيني.

من ناحية أخرى، عليك أن تضع في اعتبارك أن الخط العمودي ليس دالة ثابتة. في الواقع، الخط العمودي ليس حتى دالة، لأنه حسب التعريف، يمكن أن تحتوي الدالة على صورة واحدة فقط لكل قيمة x.

خصائص الدالة الثابتة

بعد ذلك، سوف نقوم بتحليل خصائص الدالة الثابتة. النظر في وظيفة ثابتة من أي قيمة:

$f(x)=k$

مجال الدالة الثابتة هو جميع الأعداد الحقيقية:

$\text{Dom } f = \mathbb{R}$

مسار أو نطاق الدالة الثابتة هو فقط قيمة الثابت:

$\text{Im } f= k$

وهي دالة متصلة وزوجية، لأن الدالة تأخذ دائمًا نفس القيمة:

$\displaystyle f(x)=f(-x)$

الدالة الثابتة لا تتزايد ولا تتناقص، بل هي نوع من الدالة التي يكون ميلها دائمًا صفرًا:

$m=0$

ويتقاطع دائمًا مع محور OY عند النقطة (0،k).

$(0,k)$

كل دالة ثابتة هي كثيرة الحدود من الدرجة صفر.

نعم
$k\neq 0$

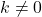
الدالة الثابتة ليس لها جذر، بدلاً من ذلك، if

$k=0$

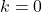
جميع الأعداد الحقيقية هي جذور الدالة الثابتة.

نهاية الدالة الثابتة عندما تقترب x زائد ما لا نهاية أو ناقص ما لا نهاية تساوي قيمة الثابت:

$\displaystyle\lim_{x\to +\infty} f(x)=k$

$\displaystyle\lim_{x\to -\infty} f(x)=k$

مشتقة الدالة الثابتة تكون دائمًا صفرًا:

$f(x)=k \ \longrightarrow \ f'(x)=0$

في الواقع، يمكن أيضًا تعريف الدالة الثابتة من فكرة المشتقة: تكون الدالة ثابتة إذا اختفت مشتقتها في مجالها بالكامل.

تكامل الدالة الثابتة هو الدالة الخطية (أو المتقاربة):

$\displaystyle \int k \ dx= x + C$

➤ انظر: ما هي الدالة الخطية؟

دالة ثابتة على فترة

لقد رأينا كيف تكون الدالة ثابتة، لكن الدالة لا يمكن أن تكون ثابتة إلا في فترة من مجالها.

من أجل فهم هذا المفهوم، تحتاج إلى معرفة الوظائف التي تم تعريفها في أجزاء، لذلك قبل المتابعة نوصي بإلقاء نظرة على الشرح التالي:

➤ انظر: ما هي الدالة متعددة التعريف؟

بمجرد أن تعرف ما هي هذه الأنواع من الوظائف، انظر إلى الوظيفة المحددة في الأجزاء الموضحة أدناه:

كما ترون من الرسم البياني، فإن الدالة ليست ثابتة عبر جميع الأرقام في مجالها. لكنها ثابتة في الفترة [-2,4)، لذا فهي دالة ثابتة في فترة واحدة فقط.

وظيفة ثابتة القضايا الثابتة

التمرين 1

حدد أي من الدوال التالية تعتبر ثوابت:

$f(x)=4\qquad g(x)=x+3\qquad h(x)=0\qquad z(x)=5x$

انظر الحل

الوظيفة الأولى،

$f(x)=4$

، هي دالة ثابتة لأنها دائمًا 4 مهما كانت القيمة التي يأخذها المتغير x.

الوظيفة الثانية،

$g(x)=x+3$

، ليست دالة ثابتة لأن قيمة الدالة تختلف باختلاف قيمة x. إنها وظيفة تقريبية.

الوظيفة الثالثة,

$h(x)=0$

، تساوي دائمًا 0 لأي قيمة لـ x، لذا فهي بالفعل دالة ثابتة.

الوظيفة الرابعة,

$z(x)=5x$

، ليست دالة ثابتة لأنها تختلف باختلاف قيمة x. إنها دالة خطية.

تمرين 2

أوجد الدالة الثابتة التي تمر بالنقطة (0.6).

انظر الحل

جبريًا، صيغة الدالة الثابتة دائمًا لها نفس الشكل:

$f(x)=k$

ومن الناحية البيانية، تكون الدالة الثابتة دائمًا خطًا أفقيًا، وبالتالي، تكون إحداثيات الدالة الثابتة دائمًا متساوية وذات قيمة

$k.$

بما أن النقطة التي تمر بها الدالة لها الإحداثيات y=6، فإن الدالة الثابتة التي نبحث عنها في هذه المشكلة يجب أن تكون:

$f(x)=6$

التمرين 3

ارسم الدوال الثابتة التالية على نفس الرسم البياني:

$f(x)=4\qquad f(x)=1\qquad f(x)=-6$

انظر الحل

لتمثيل كل دالة ثابتة، ما عليك سوى رسم خط أفقي مستقيم عند ارتفاع كل ثابت:

أمثلة على الوظائف الثابتة

اترك تعليقاً إلغاء الرد