كيفية حساب معامل المتجه

في هذه الصفحة ستشاهد شرح مقدار المتجه وكيفية حسابه مع صيغته. ستتمكن أيضًا من معرفة كيفية العثور على الوحدة من نقطتين: أصلها ونهايتها. بالإضافة إلى ذلك، سوف تكتشف كيفية تحديد مكونات المتجه من معامله وخصائص معامل المتجه. يمكنك أيضًا التدرب باستخدام الأمثلة والتمارين والمسائل خطوة بخطوة.

ما هو معامل المتجه؟

يمثل حجم المتجه المسافة بين أصله ونهايته. وبالتالي، فإن حجم المتجه يساوي طول المتجه المذكور.

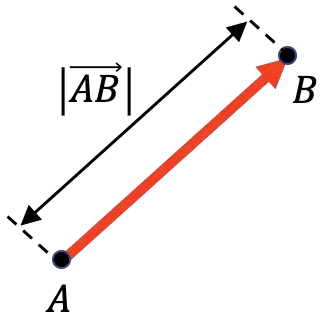
كما ترون في التمثيل البياني أعلاه، يُرمز إلى حجم المتجه بشريط عمودي على كل جانب من المتجه:

$\lvert \vv{AB}\rvert$

من ناحية أخرى، فإن معامل المتجه هو نفس معيار المتجه ، لذا يمكنك رؤيته مكتوبًا بهذه الطريقة أيضًا. ولهذا السبب يوجد علماء رياضيات يمثلون أيضًا وحدة المتجه بوجود شريطين عموديين على كل جانب:

$\lvert \lvert \vv{AB}\rvert\rvert$

صيغة لمعامل المتجه

لإيجاد مقدار المتجه في المستوى، يجب علينا تطبيق الصيغة التالية:

لتحديد مقدار المتجه، يجب علينا حساب الجذر التربيعي (الموجب) لمجموع مربعات مكوناته. بمعنى آخر، إذا كان لدينا المتجه التالي:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

وحدتها هي:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

على سبيل المثال، سوف نحسب مقدار المتجه التالي باستخدام الصيغة:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

احسب مقدار المتجه باستخدام إحداثيات أصله ونهايته

لقد رأينا للتو كيف يتم تحديد مقدار المتجه عندما نعرف مكوناته، ولكن ماذا سيحدث إذا عرفنا فقط النقاط التي يبدأ منها وأين ينتهي؟

وبالتالي، لحساب مقدار المتجه من إحداثيات أصله ونهايته، يجب عليك اتباع الخطوتين التاليتين:

أولا نجد مكونات المتجه. للقيام بذلك، علينا طرح الحد الأقصى ناقص نقطة الأصل.
ثم نحسب وحدة المتجه التي تم الحصول عليها باستخدام الصيغة التي رأيناها في القسم السابق.

دعونا نرى كيف يتم ذلك من خلال مثال:

احسب مقدار المتجه الذي أصله النقطة
$A(2,1)$

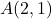
وكنقطة أخيرة

$B(-1,4).$

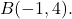
نحتاج أولًا إلى إيجاد مركبات المتجه، لذا نطرح نقطة النهاية ناقص نقطة الأصل:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

بمجرد أن نعرف المتجه، نحسب حجمه باستخدام صيغة حجم المتجه:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

ونترك النتيجة كجذر تربيعي، لأنها ليست دقيقة.

كيفية حساب مكونات المتجه من معامله

لقد رأينا كيفية استخراج مقدار المتجه من مكوناته، ولكن يمكن أيضًا عكس العملية. بمعنى آخر، يمكننا حساب مركبات المتجه من خلال معامله.

تسمى عملية العثور على مكونات المتجه من حجمه بتحلل المتجه . لذا، لتحليل المتجه، نحتاج بوضوح إلى حجمه والزاوية التي يشكلها مع محور الإحداثي السيني (المحور X).

بحيث يمكن حساب مكونات X و Y للمتجه بالنسب المثلثية:

كما ترون في الصورة، فإن حجم المتجه يشكل مثلثًا قائمًا بمكوناته، لذلك يمكن تطبيق الصيغ الأولية لعلم المثلثات.

يجب أن يؤخذ في الاعتبار أنه، على عكس معامل المتجه، يمكن أن تكون مكوناته سالبة لأن الجيب وجيب التمام يمكن أن يأخذا قيمًا سالبة.

على سبيل المثال، سنحل تحليل المتجه للمتجه الذي يكون مقداره وزاويته مع المحور OX:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

المكون الأفقي للمتجه يساوي الوحدة مضروبة في جيب تمام الزاوية:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

والمركب الرأسي للمتجه يساوي ضرب الوحدة في جيب الزاوية:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

وبالتالي فإن المتجه هو كما يلي:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

خصائص معامل المتجه

المعامل هو نوع من عمليات المتجهات التي لها الخصائص التالية:

لا يمكن أن يكون حجم المتجه سالبًا أبدًا ، بل سيكون دائمًا مساويًا أو أكبر من 0.

$\lvert \vv{\text{u}} \rvert \geq 0$

في الواقع، المتجه الوحيد الموجود بحجم صفر هو المتجه الصفري، أي المتجه

$\vv{\text{u}}= (0,0) .$

حجم حاصل ضرب المتجه بعدد حقيقي (أو عددي) يعادل ضرب القيمة المطلقة للعدد في حجم المتجه. ولذلك فإن المساواة التالية تتحقق:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

تم التحقق من عدم المساواة المثلثية : معامل مجموع متجهين أقل من أو يساوي مجموع وحداتهما بشكل منفصل.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

بالإضافة إلى ذلك، يرتبط مقدار مجموع متجهين بحاصل الضرب النقطي بالمعادلة التالية:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

حتى النصر

في الرياضيات، متجه الوحدة هو متجه معامله يساوي واحدًا.

$\lvert \vv{\text{u}} \rvert=1$

وبالتالي، فإن طول متجه الوحدة هو وحدة واحدة.

قد يبدو من الصعب جدًا أن يكون للمتجه معامل يساوي 1 بالضبط، ولكن من السهل في الواقع العثور على هذا النوع من المتجهات:

للعثور على متجه الوحدة لأي متجه، ما عليك سوى قسمته على معامله:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

ذهب

$\vv{\text{v}}_u$

هو ناقل الوحدة ل

$\vv{\text{v}},$

$\lvert \vv{\text{v}} \rvert$

الوحدة النمطية الخاصة بك.

يسمى ناقل الوحدة أيضًا بالناقل أو المتجه الطبيعي.

بالإضافة إلى ذلك، فإن متجه الوحدة له نفس اتجاه واتجاه المتجه الأصلي.

على سبيل المثال، سوف نقوم بحساب متجه الوحدة للمتجه التالي:

$\vv{\text{v}}=(1,-1)$

لتطبيع المتجه، نحتاج أولاً إلى حساب حجمه:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

وأخيرًا، نحسب متجه الوحدة عن طريق قسمة المتجه الأصلي على معامله:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

تمارين وحدة المتجهات التي تم حلها

التمرين 1

احسب حجم المتجه التالي:

$\vv{a}=(6,8)$

انظر الحل

لحساب وحدة المتجه يجب علينا تطبيق صيغته:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

تمرين 2

رتّب المتجهات التالية من الأقصر إلى الأطول.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

انظر الحل

طول المتجه يساوي حجمه. ولذلك، نحن بحاجة إلى حساب معاملات جميع المتجهات:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

وبالتالي، فإن المتجهات المرتبة من الأصغر إلى الأكبر في الطول (أو الوحدة) هي:

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

التمرين 3

تحديد مقدار المتجه الذي أصله هو النقطة

$A(-3,2)$

وكنقطة أخيرة

$B(7,-4).$

انظر الحل

لحساب الوحدة النمطية الخاصة بها، يجب عليك أولاً العثور على المتجه. للقيام بذلك، نطرح الحد الأقصى ناقص الأصل:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

بمجرد معرفة المتجه، يتم حساب معامله باستخدام صيغة المقياس:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

التمرين 4

قم بتحليل المتجه التالي وابحث عن مكوناته:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

انظر الحل

المكون الأفقي للمتجه يساوي الوحدة مضروبة في جيب تمام الزاوية:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

والمركب الرأسي للمتجه يساوي ضرب الوحدة في جيب الزاوية:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

وبالتالي فإن المتجه هو كما يلي:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

في هذه الحالة، المكونان متطابقان، أي أن زاوية ميل المتجه هي 45 درجة.

التمرين 5

احسب المتجه بنفس الاتجاه والاتجاه مثل المتجه التالي ولكن باستخدام الوحدة 1.

$\vv{a} = (-4,3)$

انظر الحل

المتجه الذي له نفس الاتجاه ونفس الاتجاه ولكن مع الوحدة 1 هو متجه الوحدة. لحسابها، نجد أولاً وحدة المتجه:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$

والآن نحسب متجه الوحدة عن طريق قسمة المتجه الأصلي على معامله:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(-4,3)}{5}= \bm{\left(-\frac{4}{5},\frac{3}{5} \right)}$

التمرين 6

قم بتحليل المتجه التالي بشكل متجهي واحسب متجه الوحدة الخاص به:

$\lvert \vv{a} \rvert =6 \qquad \alpha = 20º$

انظر الحل

أولاً، نقوم بتحليل المتجه وإيجاد إحداثياته:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(20º)= 6 \cdot 0,94 = 5,64$

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(20º)= 6 \cdot 0,34 = 2,05$

وبالتالي فإن المتجه هو كما يلي:

$\vv{a}= (5,64 \ ,\ 2,05)}$

والآن نحسب متجه الوحدة عن طريق قسمة المتجه الذي تم الحصول عليه بواسطة وحدته:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(5,64 \ ,\ 2,05)}{6}= \bm{(0,94 \ , \ 0,34) }$

لاحظ أن مكونات متجه الوحدة تساوي جيب التمام وجيب الزاوية التي يشكلها مع المحور X.

ما هو معامل المتجه؟

صيغة لمعامل المتجه

احسب مقدار المتجه باستخدام إحداثيات أصله ونهايته

كيفية حساب مكونات المتجه من معامله

خصائص معامل المتجه

حتى النصر

تمارين وحدة المتجهات التي تم حلها

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

اترك تعليقاً إلغاء الرد