جميع المتجهات المستقلة والمعتمدة خطيًا

نشرح في هذه الصفحة ما هي المتجهات المستقلة خطيًا والمعتمدة خطيًا. سترى أيضًا أمثلة لكيفية معرفة ما إذا كانت مجموعة من المتجهات تابعة أو مستقلة خطيًا. وبالإضافة إلى ذلك، ستجد تمارين ومسائل محلولة خطوة بخطوة حول الاستقلال الخطي والاعتماد.

ما هي المتجهات المستقلة خطيا؟

تكون مجموعة المتجهات الحرة مستقلة خطيًا إذا لم يكن من الممكن كتابة أي منها كمجموعة خطية من المتجهات الأخرى.

وبعبارة أخرى، نظرا لمجموعة من المتجهات

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

هذه مستقلة خطيا إذا كان الحل الوحيد للمعادلة التالية:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

هذه هي جميع المعاملات

$a_i$

يساوي 0:

$a_1=a_2=\dots = a_n=0$

هندسيًا، يكون المتجهان مستقلين خطيًا إذا لم يكن لهما نفس الاتجاه، أي إذا لم يكونا متوازيين.

للإيجاز، نقول أحيانًا بشكل مباشر أنها متجهات LI. أو أن المتجهات لها استقلال خطي.

ما هي المتجهات المعتمدة خطيا؟

من الواضح أن المتجهات المعتمدة خطيًا تعني عكس المتجهات المستقلة خطيًا. ولذلك تعريفه هو:

تعتمد مجموعة المتجهات الحرة للمستوى خطيًا إذا كان من الممكن التعبير عن أي منها كمجموعة خطية من المتجهات الأخرى التي تشكل النظام.

وبعبارة أخرى، نظرا لمجموعة من المتجهات

$\vv{\text{v}}_1, \vv{\text{v}}_2,\ldots \vv{\text{v}}_n,$

وهي تعتمد خطيا إذا كان هناك حل للمعادلة التالية:

$a_1\vv{\text{v}}_1+a_2\vv{\text{v}}_2+\dots + a_n\vv{\text{v}}_n=0$

التي لديها معامل معين

$a_i$

يختلف عن 0:

$a_i\neq 0$

والعكس صحيح أيضًا: إذا كان المتجه عبارة عن مجموعة خطية من ناقلات أخرى، فإن جميع المتجهات في المجموعة تعتمد خطيًا.

بالإضافة إلى ذلك، إذا كان هناك متجهان متوازيان، فهذا يعني أنهما يعتمدان خطيًا.

في بعض الأحيان يتم اختصارها أيضًا وتسمى ببساطة ناقلات LD. أو حتى أن المتجهات لها اعتماد خطي.

مثال لكيفية معرفة ما إذا كانت المتجهات تابعة أو مستقلة خطيًا

سنرى بعد ذلك مثالًا نموذجيًا للمتجهات المستقلة والمعتمدة خطيًا.

حدد ما إذا كانت المتجهات الثلاثة ثلاثية الأبعاد التالية لها اعتماد خطي أم استقلال:

$\vv{\text{u}} = (1,5,2)$

$\vv{\text{v}} = (-2,3,-1)$

$\vv{\text{w}} = (4,2,1)$

أولا، علينا أن نذكر شرط التركيب الخطي:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

الآن نستبدل كل متجه بإحداثياته. مثل الصفر الذي يتوافق مع المتجه الصفري:

$a_1(1,5,2)+a_2(-2,3,-1)+ a_3(4,2,1)=(0,0,0)$

تضرب المعاملات المتجهات، وبالتالي يكون التعبير التالي مكافئًا:

$(a_1,5a_1,2a_1)+(-2a_2,3a_2,-a_2) + (4a_3,2a_3,a_3)=(0,0,0)$

نضيف المتجهات:

$(a_1-2a_2+4a_3 \ , \ 5a_1+3a_2+2a_3 \ , \ 2a_1-a_2+a_3)=(0,0,0)$

إذا نظرنا عن كثب، فإن التعبير السابق يتوافق مع 3 معادلات، حيث أن كل إحداثيات المتجه الأيسر يجب أن تكون مساوية لكل إحداثيات المتجه الأيمن. وبالتالي لدينا نظام متجانس من 3 معادلات مع 3 مجهولين:

$\left. \begin{array}{l} a_1-2a_2+4a_3 = 0 \\[2ex] 5a_1+3a_2+2a_3 =0\\[2ex] 2a_1-a_2+a_3 = 0 \end{array} \right\}$

لذا فإن الشيء الوحيد الذي يتعين علينا فعله هو حل نظام المعادلات المجهولة

$a_1, a_2$

$a_3.$

للقيام بذلك، يمكنك استخدام أي طريقة (طريقة الاستبدال، طريقة غاوس، قاعدة كرامر، وما إلى ذلك). ومع ذلك، لمعرفة ما إذا كانت المتجهات هي LI أو LD يكفي تحديد ما إذا كان هناك حل آخر غير الحل التافه (جميع المعاملات تساوي الصفر). لذا:

إذا كان محدد المصفوفة المكونة من مكونات المتجهات يختلف عن الصفر، فهذا يعني أن نظام المعادلات له حل واحد فقط (
$a_1=a_2=a_3=\dots=0$

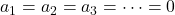
) وبالتالي فإن المتجهات مستقلة خطيًا
من ناحية أخرى، إذا كان محدد المصفوفة المكونة من مكونات المتجهات يساوي الصفر، فهذا يعني أن نظام المعادلات له أكثر من حل، وبالتالي فإن المتجهات تعتمد خطيا .

لذا فإن الشيء الوحيد الذي يجب حسابه هو المحدد بإحداثيات المتجهات (نظرًا لأنه محدد 3×3، يمكن حله باستخدام قاعدة ساروس). يتوافق هذا المحدد مع معاملات نظام المعادلات السابق:

$\displaystyle \begin{vmatrix} 1&-2&4\\[1.1ex] 5&3&2 \\[1.1ex] 2&-1&1 \end{vmatrix} = -37 \bm{\neq 0}$

في هذه الحالة، المحدد يختلف عن 0، وبالتالي فإن المتجهات مستقلة خطيًا .

ولذلك فإن الحل الوحيد الممكن لنظام المعادلات هو الحل البسيط حيث جميع المجهولات تساوي الصفر:

$a_1=a_2=a_3=0$

خصائص المتجهات المستقلة والمعتمدة خطياً

يتميز الاعتماد الخطي أو استقلال المتجهات بالخصائص التالية:

هناك متجهان متناسبان متوازيان، وبالتالي يعتمدان خطيًا لأن لهما نفس الاتجاه.

وبالمثل، إذا لم يكن للمتجهين نفس الاتجاه أو لم يكونا متناسبين، فإنهما مستقلان خطيًا.

ثلاثة نواقل مستوية (توجد في نفس المستوى) مستقلة خطيًا.

ناقل فارغة
$(\vv{\text{v}}=(0,0,0))$

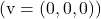
يعتمد خطيا على أي ناقل.

مجموعة من المتجهات المستقلة خطيًا تولد مساحة متجهة وتشكل أساسًا متجهًا. إذا كانت المتجهات الثلاثة متعامدة، فهي قاعدة متعامدة. وإذا كانت وحدتها تساوي أيضًا 1، فهذا يتوافق مع أساس متعامد.

حل تمارين الاعتماد الخطي والاستقلال

يوجد أدناه العديد من التمارين التي تم حلها حول المتجهات المستقلة والمعتمدة خطيًا للتدرب عليها.

التمرين 1

حدد ما إذا كانت المتجهات التالية تابعة أو مستقلة خطيًا:

$\vv{\text{u}} = (1,-2,1)$

$\vv{\text{v}} = (2,1,3)$

$\vv{\text{w}} = (5,-1,1)$

انظر الحل

نطرح أولاً شرط التركيب الخطي:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,-2,1)+a_2(2,1,3)+ a_3(5,-1,1)=(0,0,0)$

$(a_1,-2a_1,a_1)+(2a_2,a_2,3a_2) + (5a_3,-a_3,a_3)=(0,0,0)$

$(a_1+2a_2+5a_3 \ , \ -2a_1+a_2-a_3 \ , \ a_1+3a_2+a_3)=(0,0,0)$

المساواة السابقة تتوافق مع نظام المعادلات الخطية التالي:

$\left. \begin{array}{l} a_1+2a_2+5a_3 = 0 \\[2ex] -2a_1+a_2-a_3 =0\\[2ex] a_1+3a_2+a_3 = 0 \end{array} \right\}$

بعد أن ذكرنا نظام المعادلات، نحل محدد المصفوفة بحدودها:

$\displaystyle \begin{vmatrix} 1&2&5\\[1.1ex] -2&1&-1 \\[1.1ex] 1&3&1 \end{vmatrix} = -29 \bm{\neq 0}$

في هذه الحالة، يختلف المحدد عن 0، وبالتالي فإن المتجهات الثلاثة مستقلة خطيًا عن بعضها البعض.

تمرين 2

صنف المتجهات التالية على أنها تابعة أو مستقلة خطيًا:

$\vv{\text{u}} = (1,4,3)$

$\vv{\text{v}} = (-2,0,2)$

$\vv{\text{w}} = (3,-1,-4)$

انظر الحل

أولًا نطرح معادلة التركيبة الخطية:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}=0$

$a_1(1,4,3)+a_2(-2,0,2)+ a_3(3,-1,-4)=(0,0,0)$

$(a_1,4a_1,3a_1)+(-2a_2,0,2a_2) + (3a_3,-a_3,-4a_3)=(0,0,0)$

$(a_1-2a_2+3a_3 \ , \ 4a_1-a_3 \ , \ 3a_1+2a_2-4a_3)=(0,0,0)$

ومن المساواة السابقة نحصل على نظام المعادلات المتجانس التالي:

$\left. \begin{array}{l} a_1-2a_2+3a_3= 0 \\[2ex] 4a_1-a_3 =0\\[2ex] 3a_1+2a_2-4a_3 = 0 \end{array} \right\}$

بمجرد أن ذكرنا نظام المعادلات، نقوم بحل محدد المصفوفة بإحداثيات المتجهات:

$\displaystyle \begin{vmatrix} 1&-2&3\\[1.1ex] 4&0&-1 \\[1.1ex] 3&2&-4 \end{vmatrix} \bm{= 0}$

في هذه الحالة، المحدد يعادل 0، وبالتالي فإن المتجهات الثلاثة تعتمد خطيًا على بعضها البعض.

التمرين 3

بالنسبة للمتجهات الثلاثة التالية، حدد أزواج المتجهات المعتمدة خطيًا وأي الأزواج مستقلة خطيًا.

$\vv{\text{u}} = (1,2,-2) \qquad \vv{\text{v}} = (2,4,-3) \qquad \vv{\text{w}} = (-4,-8,6)$

انظر الحل

إن أبسط طريقة لمعرفة ما إذا كان زوج من المتجهات يعتمد أو مستقلاً خطيًا هو التحقق مما إذا كانا متناسبين.

نتحقق أولاً من المتجه

$\vv{\text{u}}$

مع المتجه

$\vv{\text{v}} :$

$\cfrac{1}{2} = \cfrac{2}{4} \neq \cfrac{-2}{-3} \ \longrightarrow \ \text{LI}$

ثانيا، نتحقق من المتجه

$\vv{\text{u}}$

مع المتجه

$\vv{\text{w}} :$

$\cfrac{1}{-4} = \cfrac{2}{-8} \neq \cfrac{-2}{6} \ \longrightarrow \ \text{LI}$

وأخيراً، نقوم باختبار المتجه

$\vv{\text{v}}$

مع المتجه

$\vv{\text{w}} :$

$\cfrac{2}{-4} = \cfrac{4}{-8} = \cfrac{-3}{6} = -\cfrac{1}{2} \ \longrightarrow \ \text{Proporcionales}\ \longrightarrow \ \text{LD}$

ومن ثم، فإن الزوج الوحيد من المتجهات الذي يعتمد على بعضها البعض خطيًا هو

$\vv{\text{v}}$

$\vv{\text{w}}.$

علاوة على ذلك، فإن العلاقة بينهما هي كما يلي:

$\vv{\text{v}}= -\cfrac{1}{2} \vv{\text{w}}$

أو ما يعادلها:

$\vv{\text{w}}= -2\vv{\text{v}}$

ومن ناحية أخرى، فإن أزواج المتجهات الأخرى مستقلة خطيًا.

التمرين 4

ادرس الاعتماد الخطي أو استقلال المتجهات الأربعة التالية عن بعضها البعض:

$\vv{\text{u}} = (0,1,2)$

$\vv{\text{v}} = (-1,-2,0)$

$\vv{\text{w}} = (4,1,-1)$

$\vv{\text{x}} = (-2,-3,2)$

انظر الحل

نطرح أولاً شرط التركيب الخطي:

$a_1\vv{\text{u}}+a_2\vv{\text{v}} + a_3\vv{\text{w}}+a_4\vv{\text{x}}=0$

$a_1(0,1,2)+a_2(-1,-2,0)+ a_3(4,1,-1)+a_4(-2,-3,2)=(0,0,0)$

$(0,a_1,2a_1)+(-a_2,-2a_2,0) +(4a_3,a_3,-a_3)+(-2a_4,-3a_4,2a_4)=(0,0,0)$

$(-a_2+4a_3-2a_4\ , \ a_1-2a_2+a_3-3a_4 \ , \ 2a_1-a_3+2a_4)=(0,0,0)$

في هذه الحالة لدينا نظام من 3 معادلات مع 4 مجهولين:

$\left. \begin{array}{l} -a_2+4a_3-2a_4 = 0 \\[2ex] a_1-2a_2+a_3-3a_4 =0\\[2ex] 2a_1-a_3+2a_4 = 0 \end{array} \right\}$

لا يمكننا حل محدد مصفوفة النظام بأكمله، لأنه يمكن تحديد المصفوفات المربعة فقط. لذلك يجب علينا حساب جميع المجموعات الممكنة لمحددات 3×3 ومعرفة ما إذا كانت إحداها تساوي 0، وفي هذه الحالة ستكون المتجهات معتمدة خطيًا، من ناحية أخرى، إذا كانت جميع المحددات مختلفة عن 0 فإن المتجهات الأربعة ستكون تكون مستقلة خطيا.

نحسب محدد المعاملات

$a_1, a_2$

$a_3:$