ميل الخط (الصيغة)

ستجد في هذه الصفحة الشرح الأكثر تفصيلاً لميل الخط: ما هي صيغته، أمثلة حسابية، ماذا يعني مفهوم ميل الخط،… كما ستتمكن من معرفة كيفية تحديد الميل بسهولة لخط من معادلته، وبالإضافة إلى ذلك، ستتمكن من التدرب على حل التمارين خطوة بخطوة.

صيغة لمنحدر الخط

ميل الخط يساوي الإزاحة الرأسية بين نقطتين مقسومة على الإزاحة الأفقية بين هاتين النقطتين.

أي إذا علمنا نقطتين على السطر:

$P_1(x_1,y_1) \qquad P_2(x_2,y_2)$

صيغة ميل الخط هي:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

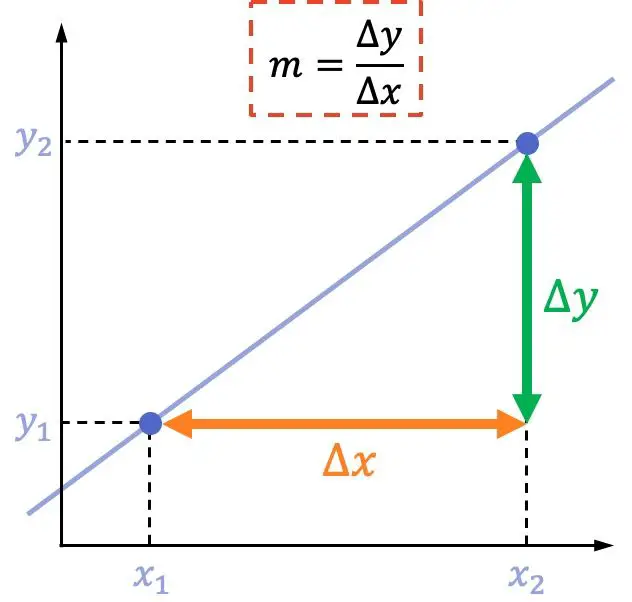
مثال لحساب ميل الخط من نقطتين

بعد ذلك، سنرى مثالاً لكيفية حساب ميل الخط باستخدام الصيغة:

احسب ميل الخط الذي يمر بالنقطتين التاليتين:

$P_1(3,1) \qquad P_2(5,7)$

للعثور على ميل هذا الخط، ما عليك سوى تطبيق صيغته:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{7-1}{5-3}=\cfrac{6}{2} = \bm{3}$

وبالتالي فإن ميل الخط يساوي 3.

إيجاد ميل الخط من معادلته

في القسم أعلاه، رأينا للتو كيفية تحديد ميل الخط عدديًا. ومع ذلك، ليس من الضروري دائمًا إجراء الحسابات، ولكن يمكن أيضًا تحديد قيمتها من معادلة الخط. يختلف كل نوع من المعادلات عن الآخر، لذلك سنقوم بتحليل كل حالة على حدة.

الميل بمعلومية المعادلة الصريحة للخط

تتبع المعادلة الصريحة للخط التعبير التالي:

$y =\color{blue}\bm{m}\color{black}x+n$

ثم المعلمة

$m$

يتوافق مع ميل الخط.

الميل نظرا لمعادلة نقطة الميل للخط

صيغة معادلة نقطة الميل للخط هي كما يلي:

$y -y_0=\color{blue}\bm{m}\color{black}(x-x_0)$

كما كان من قبل، المعامل

$m$

يتوافق مع ميل الخط.

الميل بمعلومية المعادلة الضمنية للخط

بالنظر إلى المعادلة الضمنية للخط (وتسمى أيضًا المعادلة العامة أو الديكارتية):

$Ax+By+C=0$

يمكن العثور على ميل الخط عن طريق القيام بما يلي:

$m=-\cfrac{A}{B}$

الميل مع الأخذ بعين الاعتبار متجه الاتجاه للخط

متجه اتجاه الخط هو المتجه الذي يحدد اتجاهه. لذلك، إذا كان متجه الاتجاه للخط هو:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

ميل هذا الخط هو :

$m=\cfrac{\text{v}_2}{\text{v}_1}$

الميل بمعلومية زاوية

وأخيرا، إذا كان الخط يشكل زاوية

$\alpha$

عند الجزء الموجب من محور الإحداثي السيني (المحور X)، فإن ميله يعادل ظل الزاوية:

$m = \text{tg}(\alpha)$

معنى منحدر الخط

مع كل المعلومات المذكورة أعلاه، نحن نعرف جيدًا كيفية العثور على ميل الخط. لكن في الحقيقة… ماذا يعني ميل الخط؟

يشير ميل الخط إلى الوحدات الرأسية التي يرتفعها الخط لكل وحدة أفقية في الرسم البياني.

على سبيل المثال، في تمثيل الخط التالي، يمكنك أن ترى أنه يتقدم بوحدتين رأسيتين لكل وحدة أفقية، لأن ميله يساوي 2.

بالإضافة إلى ذلك، يشير ميل الخط أيضًا إلى انحداره:

إذا كان الخط يتزايد (يرتفع)، فإن ميله يكون موجبًا.
إذا كان الخط يتناقص (تنازليًا)، فإن ميله يكون سالبًا.
إذا كان الخط أفقيًا تمامًا، فإن ميله يساوي 0.
إذا كان الخط عموديًا تمامًا، فإن ميله يساوي ما لا نهاية.

الموضع النسبي للخطوط

ومن ناحية أخرى، يمكن أيضًا معرفة الموقع النسبي بين خطين من خصائص المنحدرات:

إذا كان لخطين ميلان مختلفان، فهذا يعني أنهما متقاطعان ، أي أنهما يتقاطعان في نقطة ما.

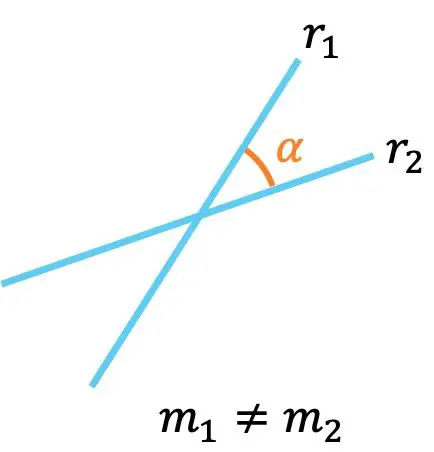
بالإضافة إلى ذلك، يمكن حساب الزاوية بين الخطين عبر ميليهما بالصيغة التالية:

$\text{tg}(\alpha) = \cfrac{m_2-m_1}{1+m_1\cdot m_2}$

ثانيا، إذا كان هناك مستقيمان لهما نفس الميل، فهذا يعني أنهما متوازيان .

وأخيرًا، فإن منحدرات الخطين المتعامدين أو المتعامدين (الذين يشكلان 90 درجة) تستوفي الشرط التالي:

هذه إحدى الطرق لمعرفة ما إذا كان الخطان متوازيين أو متعامدين مع بعضهما البعض، ولكن هناك طرق أخرى وبعضها أسرع. ولمعرفة المزيد يمكنك الذهاب إلى شرح التعامد والتوازي بين الخطوط . بالإضافة إلى ذلك، تشرح هذه الصفحات أيضًا كيفية العثور على خط متعامد (أو موازي) لخط آخر.

حل مسائل ميل الخط

التمرين 1

أوجد ميل الخط الذي يمر بالنقطتين التاليتين:

$P_1(5,6) \qquad P_2(8,3)$

انظر الحل

لحساب ميل الخط، يجب عليك استخدام الصيغة:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{3-6}{8-5}=\cfrac{-3}{3} = \bm{-1}$

تمرين 2

احسب ميل الخط الذي يمر بالنقطتين التاليتين:

$P_1(-3,1) \qquad P_2(-2,-4)$

انظر الحل

للعثور على ميل الخط، يجب عليك استخدام الصيغة:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-4-1}{-2-(-3)}=\cfrac{-5}{-2+3}=\cfrac{-5}{1} = \bm{-5}$

التمرين 3

ما هو ميل كل سطر؟

$\begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}$

انظر الحل

أ) يتم التعبير عن الخط كمعادلة ضمنية، بحيث يكون ميله 2 (المصطلح المصاحب للخط

$x$

ب) يتم تعريف الخط بمعادلة نقطة الميل، لذا فإن ميله هو 4 (الرقم الموجود قبل القوسين).

ج) الخط في صورة معادلة ضمنية، وبالتالي فإن ميله هو:

$m= - \cfrac{A}{B} = -\cfrac{6}{2} = \bm{-3}$

د) يتم تعريف الخط على شكل معادلات بارامترية، لذا يجب علينا أولاً إيجاد متجه اتجاهه ومن خلاله يمكننا حساب ميل الخط. وبالتالي فإن مكونات متجه الاتجاه هي المصطلحات المصاحبة للمعامل

$t:$

$\vv{\text{v}} = (-1,2)$

وبمجرد أن نعرف اتجاه متجه الخط، يمكننا تحديد ميل الخط:

$m = \cfrac{\text{v}_2}{\text{v}_1} = \cfrac{2}{-1} = \bm{-2}$

التمرين 4

تحديد ميل كل خط بياني:

معادلة صريحة للتمرين الخطي تم حلها خطوة بخطوة

انظر الحل

الحق الأزرق

يزداد الخط الأزرق بمقدار Y واحد لكل X، لذا فإن ميله يساوي 1.

$m=1$

الحق الأخضر

يزيد الخط الأخضر بمقدار ثلاثة Y لكل X، لذا فإن ميله هو 3 .

$m=3$

خط أحمر

يتناقص الخط الأحمر بمقدار اثنين Y لكل X، لذا فإن ميله يساوي -2 .

$m=-2$

صيغة لمنحدر الخط

مثال لحساب ميل الخط من نقطتين

إيجاد ميل الخط من معادلته

الميل بمعلومية المعادلة الصريحة للخط

الميل نظرا لمعادلة نقطة الميل للخط

الميل بمعلومية المعادلة الضمنية للخط

الميل مع الأخذ بعين الاعتبار متجه الاتجاه للخط

الميل بمعلومية زاوية

معنى منحدر الخط

الموضع النسبي للخطوط

حل مسائل ميل الخط

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد