معادلة صريحة للخط

ستجد في هذه الصفحة كل ما يتعلق بالمعادلة الصريحة للخط: ما هي، ما هي صيغتها، أمثلة حسابية، إلخ. ستجد أيضًا شرحًا تفصيليًا لما يعنيه الميل وتقاطع المعادلة الصريحة. علاوة على ذلك، سترى أمثلة مختلفة وستكون قادرًا على التدرب على التمارين التي تم حلها خطوة بخطوة.

ما هي المعادلة الصريحة للخط؟

تذكر أن التعريف الرياضي للخط هو مجموعة من النقاط المتتالية الممثلة في نفس الاتجاه بدون منحنيات أو زوايا.

إذن، معادلة الخط الصريح هي طريقة للتعبير عن أي خط رياضيًا. للقيام بذلك، تحتاج فقط إلى معرفة ميل الخط والنقطة التي يتقاطع فيها مع المحور Y.

صيغة للمعادلة الصريحة للخط

صيغة المعادلة الصريحة للخط هي:

$y=mx+n$

ذهب

$m$

هو ميل الخط و

$n$

تقاطعه y، أي الارتفاع الذي يتقاطع عنده مع المحور Y.

دعونا نرى كيف يتم حساب المعادلة الصريحة للخط من خلال مثال:

اكتب المعادلة الصريحة للخط المستقيم الذي يمر بالنقطة
$P(3,1)$

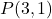
والمنحدر م = 2.

صيغة المعادلة الصريحة للخط هي:

$y= mx+n$

في هذه الحالة، تخبرنا العبارة أن ميل الخط هو m=2، وبالتالي تكون معادلة الخط كما يلي:

$y= 2x+n$

لذلك يكفي حساب المعامل n. للقيام بذلك، علينا التعويض بنقطة تنتمي إلى الخط في معادلته. وفي هذه الحالة، تخبرنا العبارة أن الخط المستقيم يمر بالنقطة

$P(3,1),$

حتى الآن:

$P(3,1)$

$y= 2x+n \ \xrightarrow{x=3 \ ; \ y=1} \ 1=2\cdot 3 +n$

ونحل المعادلة الناتجة لإيجاد قيمة n:

$1=2\cdot 3 +n$

$1=6 +n$

$1-6=n$

$-5 = n$

وبالتالي فإن المعادلة الصريحة للخط هي:

$\bm{y= 2x-5}$

ضع في اعتبارك أنه بالإضافة إلى المعادلة الصريحة، هناك طرق أخرى للتعبير عن الخط تحليليًا. على سبيل المثال، معادلة المتجه ، وهي نوع من المعادلات الخطية تختلف عن جميع المعادلات الأخرى لأنه يتم التعبير عن متجه الاتجاه ونقطة على الخط بإحداثياتهما الخاصة. في الرابط يمكنك أن ترى ما هو ولماذا هو خاص جدا.

معنى المعلمات م و ن

كما رأينا في تعريف المعادلة الصريحة للخط المعلمة

$m$

هو ميل الخط و

$n$

تقاطع y الخاص به. لكن ماذا يعني هذا؟ دعونا نرى ذلك من التمثيل الرسومي للخط:

مصطلح مستقل

$\bm{n}$

هي نقطة تقاطع الخط مع محور الكمبيوتر (محور OY). في الرسم البياني أعلاه

$n$

يساوي 1 لأن الخط يتقاطع مع المحور y عند y=1.

ومن ناحية أخرى فإن مصطلح

$\bm{m}$

يشير إلى ميل الخط ، أي ميله. كما ترون في الرسم البياني،

$m$

يساوي 2 لأن الخط يرتفع بمقدار وحدتين رأسيتين مقابل وحدة أفقية واحدة.

من الواضح أنه إذا كان الميل موجبًا فإن الدالة تتزايد (تصعد)، ومن ناحية أخرى إذا كان الميل سالبًا فإن الدالة تتناقص (تتجه لأسفل).

احسب ميل الخط

علاوة على ذلك، هناك ثلاث طرق مختلفة لتحديد ميل الخط عدديًا:

نظرا لنقطتين مختلفتين على الخط
$P_1(x_1,y_1)$

و

$P_2(x_2,y_2),$

ميل الخط يساوي:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

نعم
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

هو متجه اتجاه الخط، وميله هو:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

نعم
$\alpha$

هي الزاوية التي يشكلها الخط مع محور الإحداثي السيني (المحور X)، وميل الخط يعادل ظل الزاوية المذكورة:

$m = \text{tg}(\alpha )$

الموضع النسبي للخطوط

وأخيرًا، يُستخدم أيضًا ميل الخط لمعرفة العلاقة بين عدة خطوط. بما أن الخطين المتوازيين لهما نفس الميل، ومن ناحية أخرى، إذا كان ميل خط واحد هو المقلوب السلبي لميل خط آخر، فهذا يعني أن هذين الخطين متعامدان .

احسب المعادلة الصريحة للخط المستقيم الذي يمر بنقطتين

المشكلة النموذجية هي إيجاد المعادلة الصريحة لخط بمعلومية نقطتين يمر عبرهما. دعونا نرى كيف يتم حلها من خلال مثال:

حدد المعادلة الصريحة للخط المستقيم الذي يمر بالنقطتين التاليتين:

$P_1(4,-1) \qquad P_2(2,5)$

للعثور على المعادلة الصريحة للخط، عليك أن تعرف قيمة المعلمتين m وn. لذلك نقوم أولاً بحساب ميل الخط باستخدام صيغة النقطتين:

$m =\cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{5-(-1)}{2-4} = \cfrac{6}{-2}= -3$

$y=-3x+n$

وبعد ذلك يمكننا إيجاد تقاطع y عن طريق استبدال نقطة على الخط في المعادلة:

$P_1(4,-1)$

$y= -3x+n \ \xrightarrow{x=4 \ ; \ y=-1} \ -1=-3\cdot 4 +n$

$-1 =-12+ n$

$-1 +12= n$

$11= n$

وبالتالي فإن المعادلة الصريحة للخط هي:

$\bm{y=-3x+11}$

إيجاد المعادلة الصريحة من المعادلة الضمنية

أخيرًا، هناك نوع آخر من المشكلات التي نواجهها غالبًا وهو إيجاد المعادلة الصريحة للخط من معادلته الضمنية (وتسمى أيضًا المعادلة العامة أو الديكارتية). من الواضح، لفهم الطريقة التالية، عليك أن تعرف بالضبط ما هي المعادلة الضمنية وكيف هي؛ ولكن إذا كنت لا تتذكرها على الإطلاق، يمكنك التحقق من ذلك في الرابط.

لذا، إذا كنت تتقن بالفعل المعادلة الضمنية (أو العامة) للخط، فلنرى كيف يعمل هذا الإجراء:

أوجد المعادلة الصريحة للسطر التالي:

$3x-2y+8 =0$

كل ما علينا فعله لإيجاد المعادلة الصريحة للخط هو إيجاد المتغير

$\bm{y}.$

لذلك نحن نمرر الشروط دون

$y$

على الجانب الآخر من المعادلة:

$-2y=-3x-8$

الآن نقوم بمسح المتغير

$y:$

$\displaystyle y=\frac{-3x-8}{-2}$

وأخيرًا، نقوم بتبسيط:

$\displaystyle y=\frac{-3x}{-2} -\cfrac{8}{-2}$

$\displaystyle y=\frac{3x}{2} -(-4)$

$\displaystyle \bm{y=}\frac{\bm{3}}{\bm{2}}\bm{x +4}$

وبالتالي فإن ميل هذا الخط هو

$\displaystyle \frac{3}{2}$

وتقاطع y هو 4.

حل مشاكل المعادلات الصريحة

التمرين 1

أوجد الميل والتقاطع y للسطور التالية:

$\begin{array}{lll} A) \ y= 3x-1 & \qquad & B) \ y=5x+2 \\[2ex] C) \ y=-x+3 & \qquad & D) \ 4x+2y-6=0 \end{array}$

انظر الحل

تتبع المعادلة الصريحة للخط الصيغة التالية:

$y=mx+n$

ذهب

$m$

هو المنحدر و

$n$

الكمبيوتر في الأصل. حتى الآن:

$\bm{A)} \ y= 3x-1 \ \begin{cases} m = 3 \\[2ex] n=-1\end{cases}$

$\bm{B)} \ y= 5x+2 \ \begin{cases} m = 5 \\[2ex] n=2 \end{cases}$

$\bm{C)} \ y= -x+3 \ \begin{cases} m = -1 \\[2ex] n=3\end{cases}$

يتم التعبير عن السطر الأخير بمعادلته الضمنية، لذا نحتاج أولاً إلى تمريره إلى معادلة صريحة (حل من أجل

$y$

) ثم يمكننا تحديد المعلمات:

$\bm{D)} \ 4x+2y-6=0$

$2y =-4x+6$

$y =\cfrac{-4x+6}{2}$

$y =-2x+3$

$\begin{cases} m = -2 \\[2ex] n=3 \end{cases}$

تمرين 2

أوجد المعادلة الصريحة للخط المستقيم الذي يمر بالنقطة

$P(2,-3)$

ولها المنحدر

$m=-2.$

انظر الحل

صيغة المعادلة الصريحة للخط هي:

$y= mx+n$

في هذه الحالة، يجب أن يكون ميل الخط -2، وبالتالي فإن معادلة الخط ستكون على الشكل التالي:

$y= -2x+n$

لذلك يكفي حساب المعامل n. للقيام بذلك، يجب عليك استبدال نقطة تنتمي إلى الخط في معادلته وحل المعادلة الناتجة:

$P(2,-3)$

$y= -2x+n \ \xrightarrow{x=2 \ ; \ y=-3} \ -3=-2\cdot 2 +n$

$-3=-4 +n$

$-3+4= n$

$1= n$

باختصار، المعادلة الصريحة للخط هي:

$\bm{y= -2x+1}$

التمرين 3

أوجد المعادلة الصريحة للخط المستقيم الذي يمر بالنقطتين التاليتين:

$P_1(6,-1) \qquad P_2(3,2)$

انظر الحل

للعثور على المعادلة الصريحة للخط، عليك أن تعرف قيمة المعلمتين m وn. لذلك نحسب أولاً ميل الخط من إحداثيات النقطتين:

$m = \cfrac{\Delta y}{\Delta x}=\cfrac{y_2-y_1}{x_2-x_1} = \cfrac{2-(-1)}{3-6} = \cfrac{3}{-3}= -1$

$y=-x+n$

ثم نحدد التقاطع عن طريق استبدال نقطة على الخط في المعادلة:

$P_1(6,-1)$

$y= -x+n \ \xrightarrow{x=6 \ ; \ y=-1} \ -1=-6 +n$

$-1 +6= n$

$5= n$

وبالتالي فإن المعادلة الصريحة للخط هي:

$\bm{y=-x+5}$

التمرين 4

احسب المعادلة الصريحة للخط الذي يشكل زاوية 45 درجة مع المحور X ويمر عبر أصل الإحداثيات.

انظر الحل

إذا كان الخط يشكل زاوية 45 درجة مع المحور OX فإن ميله سيكون:

$m = \text{tg}(45º) = 1$

$y=x+n$

وبمجرد أن نعرف ميل الخط، يمكننا حساب تقاطع y عن طريق التعويض بنقطة على الخط في المعادلة. بالإضافة إلى ذلك، تخبرنا العبارة أن الخط يمر عبر نقطة الأصل الإحداثي، مما يعني أنه يمر عبر النقطة (0،0). حتى الآن:

$P(0,0)$