معادلة المحيط -

ستجد في هذه الصفحة كل ما يتعلق بمعادلة المحيط: معادلة عادية، معادلة عامة، أنواع أخرى من معادلات المحيط، عندما تكون معادلة المحيط صحيحة،… بالإضافة إلى ذلك، سترى أمثلة لكيفية العثور على المعادلة محيط ويمكنك التدرب مع التمارين المحلولة.

المعادلة العادية للدائرة

قبل معرفة ما هي معادلة المحيط، دعونا نتذكر مفهوم المحيط:

المحيط هو موضع النقاط على المستوى المتساوي البعد عن نقطة ثابتة تسمى المركز.

وبالتالي فإن جميع النقاط الموجودة في الدائرة تقع على نفس المسافة من مركزها.

بالإضافة إلى ذلك، فإن الدائرة هي أحد المقاطع المخروطية الأربعة بالإضافة إلى القطع الناقص والقطع المكافئ والقطع الزائد. أي أنه يمكن الحصول على دائرة عن طريق قطع مخروط بمستوى موازٍ لقاعدته.

إن أبسط طريقة لوصف دائرة في المستوى الديكارتي هي من معادلتها العادية. لذا فإن صيغة المعادلة العادية للمحيط هي كما يلي:

المعادلة العادية للدائرة هي:

$(x-a)^2+(y-b)^2=r^2$

ذهب:

$r$

هو نصف قطر الدائرة.
$a$

و

$b$

هي إحداثيات مركز الدائرة:

$C(a,b)$

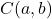
وعلى الرغم من أننا لن نوضحها لأنها مملة بعض الشيء، إلا أنه يمكن الحصول على هذه المعادلة من نظرية فيثاغورس.

دعونا نرى كيف يتم حساب المعادلة العادية للدائرة بمثال:

أوجد المعادلة العادية للدائرة التي نصف قطرها 5 ومركزها النقطة
$C(3,-1).$

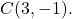
صيغة المعادلة العادية للدائرة هي:

$(x-a)^2+(y-b)^2=r^2$

لذلك، علينا فقط استبدال المجهول

$r$

بقيمة نصف القطر والمجهول

$a$

$b$

بإحداثيات X وY على التوالي لمركز الدائرة:

$(x-3)^2+(y-(-1))^2=5^2$

إذن المعادلة العادية للدائرة هي:

$\bm{(x-3)^2+(y+1)^2=25}$

المعادلة العامة للدائرة

هناك نوع آخر من معادلة المحيط وهي المعادلة العامة، وهي في الواقع الأكثر استخدامًا. وسنرى بعد ذلك كيفية الحصول على المعادلة العامة لأي محيط من معادلته العادية.

النظر في المعادلة العادية للدائرة:

$(x-a)^2+(y-b)^2=r^2$

إذا قمنا بتطوير المساواة الرائعة (أو المنتجات الرائعة):

$x^2+a^2-2ax+y^2+b^2-2by=r^2$

$x^2-2ax+y^2-2by+a^2+b^2-r^2=0$

الآن نقوم بإجراء 3 تغييرات على المتغيرات:

$A=-2a \qquad B=-2b \qquad C=a^2+b^2-r^2$

وأخيرا نحصل على المعادلة العامة للمحيط:

$x^2+y^2+Ax+By+C=0$

وبالتالي فإن صيغة المعادلة العامة للمحيط هي:

$x^2+y^2+Ax+By+C=0$

حيث يكون مركز الدائرة :

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

و نصف قطر الدائرة هو:

$\displaystyle r=\sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C}$

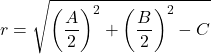
لذا، يتم الحصول على معادلة المحيط هذه دائمًا بالمعادلة العادية. فيما يلي مثال لمعرفة كيفية القيام بذلك:

أوجد المعادلة العامة للدائرة التي نصف قطرها 6 ومركزها النقطة
$C(2,4).$

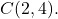
علينا أولًا إيجاد المعادلة العادية للدائرة. للقيام بذلك، نستخدم صيغته:

$(x-a)^2+(y-b)^2=r^2$

$(x-2)^2+(y-4)^2=6^2$

والآن نعمل حتى نجد المعادلة العامة للمحيط، أي حتى لا نتمكن من التبسيط:

$x^2+2^2-2\cdot x \cdot 2+y^2+4^2-2\cdot y \cdot 4=36$

$x^2+4-4x+y^2+16-8y=36$

$x^2-4x+y^2-8y+4+16-36=0$

$x^2-4x+y^2-8y-16=0$

إذن المعادلة العامة للدائرة هي:

$\bm{x^2+y^2-4x-8y-16=0}$

على الرغم من أن المشكلة لم تكن تتطلب ذلك، إلا أنه يمكننا الآن حساب مركز ونصف قطر المعادلة التي تم العثور عليها للتحقق من صحتها.

لتحديد مركز الدائرة نستخدم صيغتها:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{-4}{2}, -\frac{-8}{2}\right)$

$\displaystyle C\bigl(-(-2), -(-4)\bigr)$

$\displaystyle C\left(2,4\right)$

في الواقع، يتطابق مركز الدائرة مع مركز العبارة.

نتحقق أيضًا من نصف قطر المحيط بصيغته:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{-4}{2}\right)^2 +\left(\frac{-8}{2}\right)^2-(-16)} \\[2ex] & =\sqrt{\left(-2\right)^2 +\left(-4\right)^2+16} \\[2ex] &= \sqrt{4+16+16} \\[2ex] &= \sqrt{36} \\[2ex] & = 6 \end{aligned}$

ونصف القطر يساوي أيضًا نصف قطر العبارة. وبالتالي فإن معادلة المحيط المحسوبة صحيحة.

وجود محيط

جميع المعادلات في شكل

$x^2+y^2+Ax+By+C=0$

تتوافق مع دائرة. وبالتالي، لكي يكون هذا النوع من التعبير معادلة دائرة حقًا، يجب استيفاء الشروط الثلاثة التالية:

معاملات
$x^2$

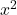
وبناءا على

$y^2$

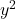
يجب أن يكونا مساويين لـ 1. ضع في اعتبارك أنه إذا كان كلا المتغيرين مسبوقًا برقم آخر ولكن كلاهما لهما نفس الرقم، فمن الممكن قسمة المعادلة بأكملها على هذا الرقم بحيث تكون معاملاتهما 1.
لا يمكن أن تحتوي المعادلة على حد
$xy.$
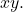
يجب أن يكون التعبير التالي إيجابيا:

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> </ol> <h2 class=$ أنواع أخرى من المعادلات الدائرة

المعادلتان الدائرتان اللتان رأيناهما، المعادلة العادية والمعادلة العامة، هما الأكثر استخداماً للتعبير رياضياً عن دائرة في المستوى (في R2). ومع ذلك، هناك عدة أنواع من المعادلات لوصف هذا الكائن الهندسي، وفيما يلي شرح لكل منها.

المعادلة الكنسية للدائرة

تُستخدم المعادلة القانونية أو المعادلة المخفضة للدائرة لوصف أي دائرة يقع مركزها عند أصل الإحداثيات ، أي عند النقطة (0،0). المعادلة المذكورة هي كما يلي:

$x^2+y^2=r^2$

بالإضافة إلى ذلك، إذا كان نصف القطر مكافئًا للوحدة (1)، فإن معادلة المحيط ستكون:

$x^2+y^2=1$

هذه المعادلة الأخيرة تتوافق مع محيط قياس الزوايا، ويسمى أيضًا محيط الوحدة أو دائرة الوحدة. وهي الدائرة التي نصف قطرها 1 ومركزها أصل الإحداثيات.

معادلات دائرتين متحدة المركز

معادلتان متحدة المركز هي تلك التي يكون مركزها في نفس النقطة. والشيء الوحيد المختلف بين الدائرتين متحدتي المركز هو نصف القطر.

ومن ثم، لكي يتحقق هذا الشرط، تكون معادلات الدائرتين متحدتي المركز متماثلتين تمامًا باستثناء حديهما المستقلين، اللذين يجب أن يكونا مختلفين.

$x^2+y^2+Ax+By+C=0$

$x^2+y^2+Ax+By+C'=0$

على سبيل المثال، الدائرتان التاليتان متحدة المركز، حيث أن جميع معاملاتهما متطابقة باستثناء الحدود المستقلة:

$x^2+y^2+3x-4y+1=0$

$x^2+y^2+3x-4y+5=0$

المعادلة البارامترية للدائرة

كما هو الحال مع الخط، يمكن أيضًا تحديد معادلة الدائرة باستخدام الدوال المثلثية للجيب وجيب التمام. وبالتالي فإن المعادلات البارامترية للدائرة هي:

$\diplaystyle \begin{cases}x= a + r \cdot \text{cos}(t) \\[2ex] y= b + r\cdot \text{sen}(t)\end{cases} \qquad t\in[0,2\pi)$

حيث النقطة

$(a,b)$

هو مركز الدائرة و

$r$

هذا هو القسم الخاص بك.

حل مسائل معادلة الدائرة

التمرين 1

احسب المعادلة العامة للدائرة التي نصف قطرها 5 ومركزها النقطة

$C(-1,2).$

انظر الحل

لإيجاد المعادلة العامة للدائرة، علينا أولًا إيجاد معادلتها العادية. للقيام بذلك، نستخدم صيغة المعادلة العادية للدائرة:

$(x-a)^2+(y-b)^2=r^2$

$(x-(-1))^2+(y-2)^2=5^2$

$(x+1)^2+(y-2)^2=25$

وبمجرد معرفة المعادلة العادية نعمل حتى نجد المعادلة العامة للدائرة:

$x^2+1^2+2\cdot x \cdot 1+y^2+2^2-2\cdot y \cdot 2=25$

$x^2+1+2x+y^2+4-4y=25$

$x^2+2x+y^2-4y+1+4-25=0$

$x^2+2x+y^2-4y-20=0$

إذن المعادلة العامة للدائرة هي:

$\bm{x^2+y^2+2x-4y-20=0}$

تمرين 2

في كل دائرة من الدوائر التالية، أوجد إحداثيات مركزها وطول نصف قطرها.

$\text{A)}\ (x-2)^2+(y+5)^2=36$

$\text{B)}\ x^2+y^2+8x-10y+1 = 0$

$\text{C)}\ x^2+y^2=4$

انظر الحل

محيط أ)

$(x-2)^2+(y+5)^2=36$

يتم التعبير عن المحيط في شكل معادلة عادية صيغتها هي:

$(x-a)^2+(y-b)^2=r^2$

وبالتالي فإن إحداثيات مركز الدائرة هي:

$C(a,b)$

$\bm{C(2,-5)}$

ونصف قطرها هو:

$r^2=36$

$\bm{r=6}$

محيط ب)

$x^2+y^2+8x-10y+1 = 0$

يتم التعبير عن هذا المحيط على شكل معادلة عامة، لذا لحساب إحداثيات مركزه يجب استخدام الصيغة التالية:

$\displaystyle C\left(-\frac{A}{2}, -\frac{B}{2}\right)$

$\displaystyle C\left(-\frac{8}{2}, -\frac{-10}{2}\right)$

$\displaystyle C\bigl(-4, -(-5)\bigr)$

$\displaystyle \bm{C(-4, 5)}$

ومن ناحية أخرى، فإن صيغة العثور على نصف قطر الدائرة هي:

$\displaystyle \begin{aligned} r & = \sqrt{\left(\frac{A}{2}\right)^2 +\left(\frac{B}{2}\right)^2-C} \\[2ex] & =\sqrt{\left(\frac{8}{2}\right)^2 +\left(\frac{-10}{2}\right)^2-1} \\[2ex] & =\sqrt{\left(4\right)^2 +\left(-5\right)^2-1} \\[2ex] &= \sqrt{16+25-1} \\[2ex] &= \bm{\sqrt{40}} \end{aligned}$

محيط ج)

$x^2+y^2=4$

يتم التعبير عن المحيط في شكل معادلة عادية صيغتها هي:

$(x-a)^2+(y-b)^2=r^2$

وبالتالي فإن إحداثيات مركز الدائرة هي:

$C(a,b)$

في هذه الحالة، المعادلة ليس لها حد.

$a$

لا

$b,$

لذلك يتمحور حول أصل الإحداثيات:

$\bm{C(0,0)}$

ونصف قطرها هو:

$r^2=4$

$\bm{r=2}$

التمرين 3

أي المعادلات التالية هي معادلة الدائرة؟

$\text{A)}\ x^2+y^2+4x-6y-1=0$

$\text{B)}\ x^2+y^2+5x+5y+2xy-4 = 0$

$\text{C)}\ 2x^2+2y^2-8x+4y+2=0$

$\text{D)}\ x^2+y^2+x+2y+6=0$

انظر الحل

لكي يكون التعبير معادلة دائرة، يجب أن تكون الشروط التالية صحيحة:

1. معاملات

$x^2$

وبناءا على

$y^2$

يجب أن تكون مساوية لـ 1.
2. لا يمكن أن تحتوي المعادلة على حد

$xy.$

$\displaystyle \left(\frac{A}{2}\right)^2+\left(\frac{B}{2}\right)^2-C>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”190″ style=”vertical-align: -17px;”> <p class=$ ولذلك يجب علينا التحقق من استيفاء الشروط الثلاثة لكل معادلة.

المعادلة أ)

$x^2+y^2+4x-6y-1=0$

معاملات

$x^2$

$y^2$

هي 1 والمعادلة ليس لها حد

$xy.$

ويكفي إذن التحقق من الشرط الثالث:

$\displaystyle \left(\frac{4}{2}\right)^2+\left(\frac{-6}{2}\right)^2-(-1)>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”216″ style=”vertical-align: -17px;”> <p style=$

$\displaystyle 2^2+\left(-3\right)^2+1>0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”146″ style=”vertical-align: -5px;”> <p style=$

$\displaystyle 4+9+1>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> <p style=$

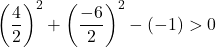
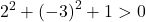
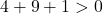
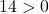$\displaystyle 14>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”49″ style=”vertical-align: -2px;”> <p class=$ المعادلة تحقق الشروط الثلاثة فهي معادلة دائرة.

المعادلة ب)

$x^2+y^2+5x+5y+2xy-4 = 0$

المعادلة لها حد مع

$xy,$

التي لا تتوافق معها المعادلة مع دائرة.

المعادلة ج)

$2x^2+2y^2-8x+4y+2=0$

معاملات

$x^2$

$y^2$

ليست 1، ولكن يمكننا تحويل المعادلة عن طريق قسمة جميع الحدود:

$x^2+y^2-4x+2y+1=0$

بهذه الطريقة الآن معاملات

$x^2$

$y^2$

نعم هم 1، وعلاوة على ذلك، فإن المعادلة ليس لها حد

$xy.$

فلا يبقى لنا إذن إلا أن نؤكد الشرط الثالث:

$\displaystyle \left(\frac{-4}{2}\right)^2+\left(\frac{2}{2}\right)^2+1>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”189″ style=”vertical-align: -17px;”> <p style=$

$\displaystyle (-2)^2+\left(1\right)^2+1>0″ title=”Rendered by QuickLaTeX.com” height=”22″ width=”158″ style=”vertical-align: -5px;”> <p style=$

$\displaystyle 4+1+1>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”103″ style=”vertical-align: -2px;”> <p style=$

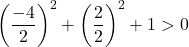
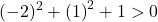
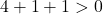
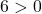$\displaystyle 6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> <p class=$ المعادلة تحقق الشروط الثلاثة فهي معادلة دائرة.

المعادلة د)

$x^2+y^2+x+2y+6=0$

معاملات

$x^2$

$y^2$

هي 1 والمعادلة ليس لها حد

$xy.$

ويكفي إذن التحقق من الشرط الثالث:

$\displaystyle \left(\frac{1}{2}\right)^2+\left(\frac{2}{2}\right)^2-6>0″ title=”Rendered by QuickLaTeX.com” height=”47″ width=”175″ style=”vertical-align: -17px;”> <p style=$

$\displaystyle 0,25+1-6>0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”128″ style=”vertical-align: -4px;”> <p style=$

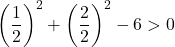
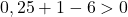
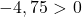$\displaystyle -4,75 \ \cancel{>} \ 0″ title=”Rendered by QuickLaTeX.com” height=”17″ width=”82″ style=”vertical-align: -4px;”> <p class=$ المعادلة لا تحقق الشرط الأخير، لذا فهي ليست معادلة دائرة .

التمرين 4

حدد معادلة الدائرة التي تمر بالنقاط الثلاث التالية:

$A(0,0) \quad B(3,0) \quad C(2,-2)$

انظر الحل

المعادلة العامة لأي دائرة هي:

$x^2+y^2+Ax+By+C=0$

ومن ثم، علينا التعويض بإحداثيات النقاط في معادلة الدائرة لإيجاد المعلمات

$A,$

$B$

$C.$

بالنقطة الأولى نجد المعامل

$C:$

$A(0,0) \ \longrightarrow \ 0^2+0^2+A\cdot 0 +B\cdot 0+C=0 \ \longrightarrow \ \bm{C = 0}$

بالنقطة الثانية نجد المعامل

$A:$

$\begin{aligned}A(3,0) \ \longrightarrow \ & 3^2+0^2+A\cdot 3 +B\cdot 0+C=0 \\[2ex] & 9+A\cdot 3 =0\\[2ex]& \bm{A=-3} & \end{aligned}$

ومن النقطة الثالثة نجد المعامل

$B:$

$\begin{aligned} A(2,-2) \ \longrightarrow \ & 2^2+(-2)^2+A\cdot 2 +B\cdot (-2)+C=0 \\[2ex] & 4+4+(-3)\cdot 2+ B\cdot (-2)+0=0 \\[2ex] & 8-6-2B=0 \\[2ex] & \bm{B=1} \end{aligned}$

في الختام، المعادلة العامة للمحيط هي:

$\bm{x^2+y^2-3x+y=0}$

التمرين 5

إذا كان طرفا الدائرة المتقابلان هما النقطتان التاليتان:

$A(2,3) \qquad B(6,-1)$

ما هي المعادلة العادية للدائرة؟

انظر الحل

إذا كانت النقطتان هما طرفا الدائرة، فإن مركزها يكون نقطة المنتصف بين هاتين النقطتين:

$\displaystyle C\left(\frac{2+6}{2} , \frac{3+(-1)}{2} \right)$

$\displaystyle C\left(\frac{8}{2} , \frac{2}{2} \right)$

$\displaystyle C\left(4,1 \right)$

من ناحية أخرى، سيكون قطر الدائرة هو المسافة بين النقطتين، والتي يمكن حسابها باستخدام مقدار المتجه الذي تشكله النقطتان:

$\vv{AB} = B-A=(6,-1) - (2,3) = (4,-4)$

$d = \lvert \vv{AB} \rvert =\sqrt{4^2+(-4)^2} = \sqrt{16+16} = \sqrt{32}$

ونصف قطر الدائرة هو نصف القطر:

$r = \cfrac{\sqrt{32}}{2}$

وبالتالي فإن المعادلة العادية للدائرة هي:

$(x-a)^2+(y-b)^2=r^2$

$\displaystyle (x-4)^2+(y-1)^2=\left(\frac{\sqrt{32}}{2}\right)^2$

$\displaystyle \bm{(x-4)^2+(y-1)^2=}\frac{\bm{32}}{\bm{4}}$

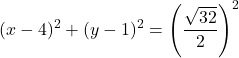
أخيرًا، إذا كانت هذه المقالة مفيدة لك، فمن المؤكد أنك ستهتم أيضًا بصفحات القطع الزائد (الرياضيات) والقطع المكافئ (الرياضيات) . ستجد شرحا مفصلا لماهية القطع الزائد والقطع المكافئ ومعادلاتهما وخصائصهما وأمثلة وتمارين محلولة…

المعادلة العادية للدائرة

المعادلة العامة للدائرة

وجود محيط

المعادلة الكنسية للدائرة

معادلات دائرتين متحدة المركز

المعادلة البارامترية للدائرة

حل مسائل معادلة الدائرة

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد