مصفوفة لا إرادية

في هذه الصفحة سوف تتعلم ما هي المصفوفة الملتوية. نعرض لك أيضًا أمثلة على المصفوفات الملزمة للأبعاد 2×2 و3×3 و4×4. وأخيرًا، ستجد صيغة المصفوفة غير الملتوية.

ما هي المصفوفة غير الملتوية؟

معنى المصفوفة اللاإرادية هو كما يلي:

تعريف المصفوفة الالتفافية : مصفوفة مربعة قابلة للعكس ومصفوفتها العكسية هي المصفوفة نفسها.

$A^{-1} = A$

ذهب

$A$

هو أي مصفوفة و

$A^{-1}$

يمثل معكوسه.

من الواضح أن المصفوفة غير الملتوية هي مثال لمصفوفة عادية أو غير متدهورة .

إذا كنت لا تعرف ما هو معكوس المصفوفة، يمكنك أن ترى هنا كيفية حساب المصفوفة العكسية 3×3 . من المهم معرفة كيفية قلب المصفوفة، ولكن لهذا تحتاج أيضًا إلى معرفة كيفية حساب المصفوفة المجاورة .

لكن العودة إلى الموضوع: عندما تكون المصفوفة غير حلقية، فإن ضرب المصفوفة بالمصفوفة نفسها يعطي مصفوفة الهوية. ألق نظرة على العرض التوضيحي:

أي مصفوفة مضروبة في معكوسها تعطي مصفوفة الهوية (أو الوحدة). لذا:

$\displaystyle A \cdot A^{-1} = I$

وبما أن معكوس المصفوفة الالتفافية هو المصفوفة نفسها:

$\displaystyle A \cdot A = I$

وبالتالي، فإن المصفوفة التربيعية غير الملتوية تعطي مصفوفة الهوية:

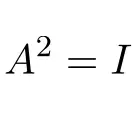
أمثلة على المصفوفات الالتفافية

مثال لمصفوفة حلزونية 2×2:

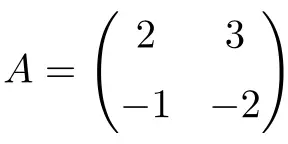
يمكننا التحقق من أنها مصفوفة لاالتفافية عن طريق حساب القوة الثانية للمصفوفة:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

بما أن المصفوفة A تربيع هي مصفوفة الهوية، فإن المصفوفة A هي مصفوفة ارتدادية 2×2.

مثال لمصفوفة حلزونية 3×3:

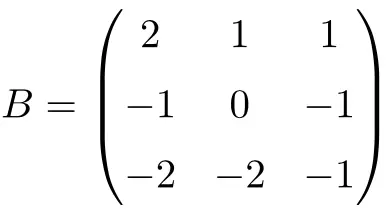
يمكننا التحقق من أنها مصفوفة لاالتفافية عن طريق حل منتج المصفوفة بمفردها:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

بما أن المصفوفة B تربيع هي مصفوفة الهوية، فإن المصفوفة B هي مصفوفة ارتدادية 3×3.

مثال لمصفوفة حلقية 4×4:

مصفوفة الهوية (أو الوحدة)، مهما كان أبعادها، هي بحكم تعريفها مصفوفة لاالتفافية.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

يمكننا التحقق من أنها مصفوفة لاالتفافية عن طريق رفع المصفوفة إلى 2:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

بما أن مصفوفة الهوية المربعة هي مصفوفة الهوية، فإن مصفوفة الهوية هي مصفوفة ارتدادية 4×4.

من الواضح أن مصفوفة الهوية يمكن أن تكون بأي بعد، لأنها مجرد مصفوفة قطرية بها جميع الأرقام 1 على القطر الرئيسي والباقي 0. لذا فإن مصفوفة الهوية ستكون دائمًا مصفوفة غير ملتوية، مهما كان ترتيبها.

صيغة المصفوفة المتضمنة

من خصائص المصفوفة الالتفافية إمكانية معرفة صيغتها. لكن إثبات صيغة المصفوفة الالتفافية من الدرجة الثانية أمر ممل للغاية، لذلك سنتركك مباشرة للنتيجة، وهذا هو المهم حقًا. إذا كنت مهتمًا أكثر بالعرض التوضيحي، فيمكنك رؤيته مشروحًا خطوة بخطوة أدناه في التعليقات.

صيغة المصفوفة الملزمة للبعد 2 × 2 هي كما يلي:

ولذلك، فإن أي مصفوفة تكون قيم قطرها الرئيسية متقابلة ومحددها هو -1، ستكون مصفوفة لاالتفافية.

ومع ذلك، بالإضافة إلى المصفوفات الموصوفة في هذه الصيغة، يجب أن يؤخذ في الاعتبار أن مصفوفة الهوية وعكسها هي أيضًا مصفوفات لاالتفافية من الرتبة 2:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

خصائص المصفوفة الملتفة

المصفوفات غير الملتوية لها الخصائص التالية:

محدد المصفوفة الالتفافية يساوي دائمًا -1 أو +1.

هناك علاقة بين المصفوفات اللاالتفافية والمصفوفات العاجزة : المصفوفة
$A$

يكون غير التفافي إذا وفقط إذا كانت المصفوفة

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

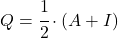
هو عاجز.

نعم
$A$

و

$B$

هما مصفوفتان انتقاليتان متبادلتان، ثم حاصل ضرب المصفوفة

$AB$

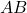
هي أيضًا مصفوفة التفافية أخرى.

أي قوة للمصفوفة الالتفافية تؤدي إلى مصفوفة لاالتفافية أخرى. على وجه الخصوص، المصفوفة غير الملتوية المرفوعة إلى أس فردي ستكون مساوية لنفسها، من ناحية أخرى، إذا تم رفعها إلى أس زوجي فستكون مكافئة لمصفوفة الهوية.

$A^2 = I$

$A^3 = A$