▷ مشتق المنتج (الصيغة والتدريبات المحلولة)

نوضح في هذه المقالة كيفية اشتقاق منتج وظيفتين (الصيغة). بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة على مشتقات حواصل ضرب الدوال وحتى التدرب على حل التمارين على مشتقات الضرب.

صيغة مشتق المنتج

مشتقة منتج دالتين مختلفتين يساوي منتج مشتقة الدالة الأولى في الدالة غير المتمايزة الثانية بالإضافة إلى منتج الدالة غير المتمايزة الأولى في مشتق الوظيفة الثانية.

بمعنى آخر، إذا كانت f(x) و g(x) دالتين مختلفتين، فإن صيغة مشتق الضرب بين الدالتين هي كما يلي:

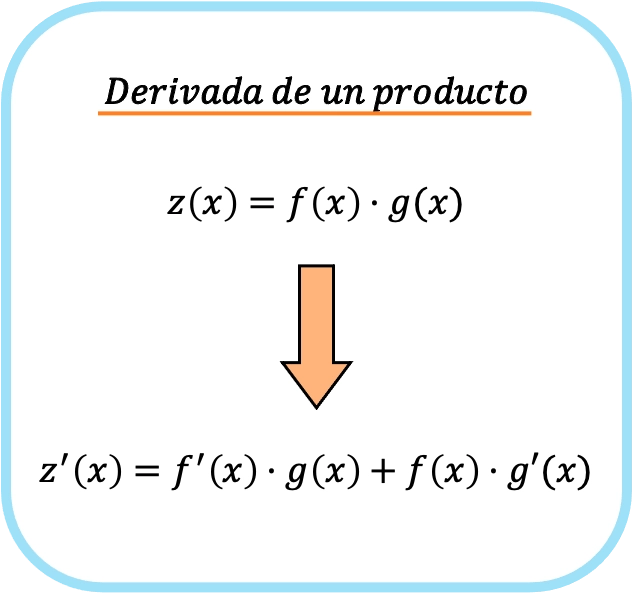
وهكذا، من خلال تطبيق قاعدة مشتقة المنتج، ننتقل من الضرب البسيط إلى منتجين مختلفين.

أمثلة على مشتقات المنتج

بمجرد أن نعرف ما هي صيغة مشتقة المنتج (أو الضرب)، فسنقوم بحل عدة أمثلة لهذا النوع من المشتقات. وهذا سيجعل الأمر أسهل بكثير بالنسبة لك لفهم كيفية اشتقاق منتج من وظيفتين.

مثال 1

في هذا المثال، سنحل مشتقة دالتين محتملتين عن طريق الضرب:

$f(x)=5x^2\cdot (x^3+4x-6)$

كما رأينا في القسم السابق، فإن صيغة مشتقة الضرب هي:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

لذلك، يجب علينا أولاً حساب مشتقة كل دالة على حدة:

$\cfrac{d}{dx}\ 5x^2=10x$

$\cfrac{d}{dx}\ (x^3+4x-6)=3x^2+4$

وبمجرد معرفة مشتقة كل دالة، يمكننا تطبيق صيغة مشتقة حاصل ضرب دالتين. أي أننا نضرب مشتقة العامل الأول في العامل الثاني دون اشتقاق، ثم نضيف حاصل ضرب العامل الأول دون اشتقاق في مشتقة العامل الثاني:

$\begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}$

أخيرًا، نقوم بتنفيذ العمليات لتبسيط النتيجة التي تم الحصول عليها:

$\begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}$

مثال 2

في هذه الحالة سوف نشتق حاصل ضرب الثابت بواسطة دالة:

$f(x)=7\cdot (x^2+3x)$

القاعدة المشتقة للمنتج هي كما يلي:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

وبالتالي، فإننا نشتق بشكل منفصل كل وظيفة تشكل جزءًا من المنتج:

$\cfrac{d}{dx}\ 7=0$

$\cfrac{d}{dx}\ (x^2+3x)=2x+3$

ثم نطبق قاعدة مشتقة الضرب:

$\begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}$

لاحظ أن مشتقة الثابت تكون دائمًا صفرًا، لذلك يمكننا استنتاج أن مشتقة ضرب ثابت في دالة تساوي حاصل ضرب الثابت ومشتقة الدالة.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=k\cdot f(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=k\cdot f'(x)\end{array} \end{empheq}$

مثال 3

دعونا نحل المنتج بين الدالة الأسية واللوغاريتم الطبيعي:

$f(x)=4^{3x}\cdot \ln(x^2)$

صيغة مشتق ضرب وظيفتين هي:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

لذلك يجب علينا أولاً أن نقوم بعمل مشتقة كل دالة تشكل المنتج بشكل منفصل، وهي كما يلي:

$\cfrac{d}{dx}\ 4^{3x}=4^{3x}\cdot \ln (4) \cdot 3$

$\cfrac{d}{dx}\ \ln(x^2)=\cfrac{2x}{x^2}=\cfrac{2}{x}$

وبالتالي فإن المنتج المشتق من الوظائف هو:

$\begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}$

تمارين محلولة على مشتقة المنتج

يشتق المنتجات الوظيفية التالية:

$\text{A) }f(x)=5\ln(3x)$

$\text{B) }f(x)=(4x^2+1)(6x^3-7)$

$\text{C) }f(x)=\text{cos}(4x)\cdot e^{x^2}$

$\text{D) }f(x)=(3x^3-4x^2+8x)\cdot \sqrt{6x^2+3x}$

$\text{E) }f(x)=5^{4x}\cdot \log_9(x^3-x)$

$\text{F) }f(x)=\left(10x^6-6x^5\right)^4\cdot \text{arcsen}(x^2+9x)$

انظر الحل

$\text{A) } f'(x)=5\cdot \cfrac{3}{3x} =\cfrac{5}{x}$

$\begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}$

$\text{C) }f'(x) =-4\text{sen}(4x)\cdot e^{x^2}+\text{cos}(4x)\cdot e^{x^2}\cdot 2x$

$\text{D) }f'(x)=(9x^2-8x+8)\cdot \sqrt{6x^2+3x}+(3x^3-4x^2+8x)\cdot\cfrac{12x+3}{2\sqrt{6x^2+3x}}$

$\text{E) }f'(x)=5^{4x}\cdot \ln(5) \cdot 4 \cdot \log_9(x^3-x)+ 5^{4x}\cdot\cfrac{3x^2-1}{(x^3-x)\ln(9)}$

$\begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}$

مشتقة من منتج ثلاثي الوظائف

بعد ذلك، نتركك مع صيغة مشتقة ضرب 3 دوال، لأنها تشبه إلى حد كبير صيغة مشتقة دالتين ويمكن أن تكون مفيدة في بعض الحالات.

مشتقة حاصل ضرب ثلاث دوال تساوي حاصل ضرب مشتقة الدالة الأولى والدالتين الأخريين، بالإضافة إلى حاصل ضرب مشتقة الدالة الثانية والدالات الأخريين، بالإضافة إلى حاصل ضرب مشتقة الدالة الوظيفة الثالثة. تعمل بواسطة الوظيفتين الأخريين.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=1mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=f(x)\cdot g(x)\cdot h(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)\cdot h(x)+f(x)\cdot g'(x)\cdot h(x)+f(x)\cdot g(x)\cdot h'(x)\end{array} \end{empheq}$

على سبيل المثال، إذا أردنا استخلاص الضرب التالي لثلاث دوال مختلفة:

$f(x)=3x\cdot e^{2x} \cdot \text{sen}(x)$

لحل المشتقة، يجب علينا تطبيق قاعدة مشتقة منتج ثلاث وظائف، وبالتالي:

$f'(x)=3\cdot e^{2x} \cdot \text{sen}(x)+3x\cdot 2e^{2x} \cdot \text{sen}(x)+3x\cdot e^{2x} \cdot \text{cos}(x)$

عرض صيغة مشتق المنتج

وأخيرًا، سنوضح صيغة مشتقة الضرب. ليس عليك أن تحفظها، ولكن من الجيد دائمًا أن تفهم من أين تأتي الصيغ. 🙂

من التعريف الرياضي للمشتق:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

دع الدالة z تكون حاصل ضرب دالتين مختلفتين:

$z(x)=f(x)\cdot g(x)$

إذن مشتقة z حسب التعريف ستكون:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)\cdot g(x+h)\bigr]-\bigl[f(x)\cdot g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

وكما نعلم، إذا أضفنا حدًا بالجمع والطرح، فإن ذلك لا يؤثر على النتيجة طالما أن كلاهما هو نفس الحد. لذلك يمكننا الانتقال إلى الخطوة التالية:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)\color{orange}\bm{-f(x+h)\cdot g(x)+f(x+h)\cdot g(x)}\color{black}-f(x)\cdot g(x)}{h}$

نستخدم الآن خصائص الحدود لفصل الحد السابق إلى حدين مختلفين:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x+h)\cdot g(x)}{h}+\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x)}{h}$

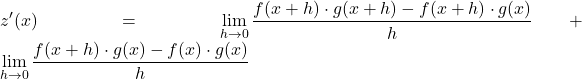
نستخرج العامل المشترك في بسط الكسرين:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\bigl(g(x+h)-g(x)\bigr)}{h}+\lim_{h \to 0}\frac{g(x)\bigl(f(x+h)-f(x)\bigr)}{h}$

ومن ناحية أخرى، فإننا نعرف نتيجة النهاية التالية:

$\displaystyle \lim_{h \to 0}f(x+h)=f(x)$

وبالتالي يمكننا تبسيط الحدود:

$\displaystyle z'(x)=\lim_{h \to 0}f(x+h)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+\lim_{h \to 0}g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$\displaystyle z'(x)=f(x)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

وأخيرًا، بالنظر إلى الحدين المتبقيين، فإن كل منهما يتوافق مع تعريف مشتقة الدالة. وبالتالي يمكن تبسيط المساواة:

$\displaystyle z'(x)=f(x)\cdot g'(x)+g(x)\cdot f'(x)$

أو ما يعادلها:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{empheq}$

مشتق من المنتج (أو الضرب)

صيغة مشتق المنتج

أمثلة على مشتقات المنتج

مثال 1

مثال 2

مثال 3

تمارين محلولة على مشتقة المنتج

مشتقة من منتج ثلاثي الوظائف

عرض صيغة مشتق المنتج

اترك تعليقاً إلغاء الرد