مشتق قاطع التمام

نشرح في هذه المقالة كيفية اشتقاق قاطع التمام للدالة (الصيغة). ستجد أيضًا تمارين محلولة خطوة بخطوة لمشتقة قاطع التمام. وأخيرًا، ستتمكن من مشاهدة عرض توضيحي لصيغة هذا النوع من المشتقات المثلثية.

صيغة مشتقة كوزيكانت

مشتق قاطع التمام لـ x يساوي ناقص حاصل جيب التمام لـ x مقسومًا على مربع جيب التمام لـ x.

$f(x)=\text{cosec}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}$

باستخدام الصيغ المثلثية، يمكننا أيضًا تحديد مشتق قاطع التمام لـ x مطروحًا منه ناتج ظل التمام لـ x في قاطع التمام لـ x.

$f'(x)=-\cfrac{\text{cos}(x)}{\text{sen}^2(x)}=-\cfrac{\text{cos}(x)}{\text{sen}(x)}\cdot \cfrac{1}{\text{sen}(x)}=-\text{cot}(x)\cdot \text{cosec}(x)$

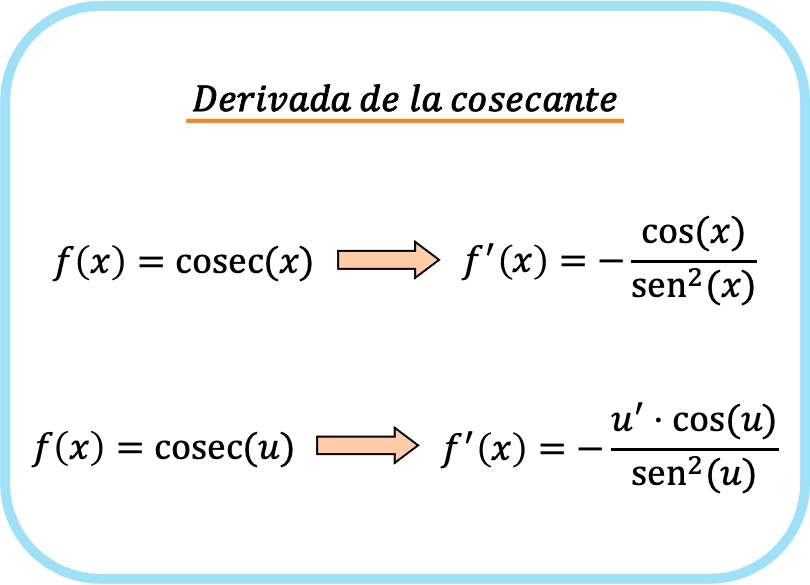
وإذا طبقنا قاعدة السلسلة، فإن مشتقة قاطع تمام الدالة تساوي حاصل ضرب مشتقة الدالة في جيب تمام الدالة مقسومًا على مربع جيب الدالة.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

وبالتالي فإن الصيغة المستخدمة لاشتقاق قاطع التمام للدالة هي كما يلي:

أمثلة على مشتق قاطع التمام

بعد أن رأينا صيغة مشتقة قاطع التمام، سنقدم الآن عدة أمثلة. لذلك يمكنك أن ترى بالضبط كيف يتم اشتقاق قاطع التمام للدالة.

مثال 1: مشتق قاطع التمام 2x

في هذا المثال سوف نرى كم هو مشتق قاطع التمام 2x:

$f(x)=\text{cosec}(2x)$

تختلف دالة وسيطة قاطع التمام عن x، لذا نحتاج إلى استخدام قاعدة مشتقة قاطع التمام مع قاعدة السلسلة.

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

لذا، للعثور على مشتق هذه الدالة المثلثية، ما عليك سوى استبدال القيم في الصيغة السابقة: في وسيطة جيب التمام والجيب، نضع 2x، وu’ يتوافق مع مشتق 2x، أي 2:

$f(x)=\text{cosec}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2\cdot \text{cos}(2x)}{\text{sen}^2(2x)}$

مثال 2: مشتق قاطع التمام لـ x تربيع

في هذا التمرين، سنرى مقدار مشتقة قاطع التمام لـ x تربيع:

$f(x)=\text{cosec}(x^2)$

منطقيًا، يتم حل مشتقة هذه الدالة المثلثية باستخدام صيغة مشتق قاطع التمام:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

مشتق x تربيع يعطي 2x، وبالتالي فإن مشتق قاطع تمام x أس اثنين هو:

$f(x)=\text{cosec}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x\cdot \text{cos}(x^2)}{\text{sen}^2(x^2)}$

مثال 3: مشتقة قاطع التمام المكعب للدالة الأسية

$f(x)=\text{cosec}^3(e^{5x})$

مهما كانت وسيطة الدالة، فإن قاعدة مشتقة قاطع التمام للدالة هي:

$f(x)=\text{cosec}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'\cdot \text{cos}(u)}{\text{sen}^2(u)}$

لكن في هذه الحالة لدينا دالة مركبة، لأن قاطع التمام مرفوع إلى ثلاثة، علاوة على ذلك، توجد في سعتها دالة أسية. لذا، للتمييز بين الدالة بأكملها، نحتاج إلى تطبيق قاعدة السلسلة عدة مرات:

$\begin{aligned}\displaystyle f'(x)& = 3\text{cosec}^2(e^{5x})\cdot\left(-\frac{5e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\right)\\[1.5ex]&=-\frac{-15\text{cosec}^2(e^{5x})\cdot e^{5x}\cdot \text{cos}(e^{5x})}{\text{sen}^2(e^{5x})}\end{aligned}$

حل مسائل مشتق قاطع التمام

اشتق وظائف قاطع التمام التالية:

$\text{A) }f(x)=\text{cosec}(x^4-2x^2)$

$\text{B) }f(x)=\text{cosec}(x^3+e^x-10)$

$\text{C) }f(x)=\text{cosec}\bigl(\ln(x^3+7x^2)\bigr)$

$\text{D) }f(x)=\text{cosec}\bigl(\text{arccos}(x^7)\bigr)$

$\text{E) }f(x)=\text{cosec}\left(\sqrt{9x^2-4x}\right)$

انظر الحل

$\text{A) }f('x)=-\cfrac{(4x^3-4x)\cdot \text{cos}(x^4-2x^2)}{\text{sen}^2(x^4-2x^2)}$

$\text{B) }f('x)=-\cfrac{(3x^2+e^x)\cdot \text{cos}(x^3+e^x-10)}{\text{sen}^2(x^3+e^x-10)}$

$\begin{aligned}\text{C) }f'(x)& =-\cfrac{\cfrac{3x^2+14x}{x^3+7x^2}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{\cfrac{3x+14}{x^2+7x}\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{\text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\\[1.5ex] &= -\cfrac{(3x+14)\cdot \text{cos}\bigl(\ln(x^3+7x^2)\bigr)}{(x^2+7x)\cdot \text{sen}^2\bigl(\ln(x^3+7x^2)\bigr)}\end{aligned}$

$\begin{aligned}\text{D) }f'(x)& =-\cfrac{-\cfrac{7x^6}{\sqrt{1-\left(x^7\right)^2}}\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =-\cfrac{(-7x^6)\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\\[1.5ex] & =\cfrac{7x^6\cdot \text{cos}\bigl(\text{arccos}(x^7)\bigr)}{\left(\sqrt{1-x^{14}}\right)\cdot \text{sen}^2\bigl(\text{arccos}(x^7)\bigr)}\end{aligned}$

$\begin{aligned} \text{E) }f'(x)& =-\cfrac{\cfrac{18x-4}{2\cdot\sqrt{9x^2-4x}} \cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{\text{sen}^2\left(\sqrt{9x^2-4x}\right)}\\[1.5ex] &=-\cfrac{(18x-4)\cdot \text{cos}\left(\sqrt{9x^2-4x}\right)}{2\sqrt{9x^2-4x}\cdot \text{sen}^2\left(\sqrt{9x^2-4x}\right)} \end{aligned}$

إثبات صيغة مشتق قاطع التمام

بعد ذلك، سنوضح صيغة مشتقة قاطع التمام. على عكس العروض التوضيحية الأخرى، في هذه الحالة لن نستخدم النهاية التي تحدد المشتقة، لكننا سنبدأ من التعريف الرياضي لقاطع التمام.

جبريًا، الدالة المثلثية قاطع التمام هي المعكوس الضربي للجيب:

$f(x)=\text{cosec}(x)=\cfrac{1}{\text{sen}(x)}$

يمكننا إذن أن نأخذ مشتقة قاطع التمام باستخدام قاعدة خارج القسمة:

$f'(x)=\cfrac{0\cdot \text{sen}(x)-1\cdot \text{cos}(x)}{\text{sen}^2(x)}$

$f'(x)=\cfrac{-\text{cos}(x)}{\text{sen}^2(x)}$

كما ترون، فقط من خلال تطبيق قاعدة مشتقة القسمة نصل إلى صيغة مشتقة قاطع التمام. وبما أن مشتقة خارج القسمة مثبتة بالفعل (يمكنك رؤيتها في الرابط التالي)، فقد تم إثبات قاعدة مشتقة قاطع التمام أيضًا.

➤ انظر: إثبات مشتقة خارج القسمة

مشتق من قاطع التمام

صيغة مشتقة كوزيكانت

أمثلة على مشتق قاطع التمام

مثال 1: مشتق قاطع التمام 2x

مثال 2: مشتق قاطع التمام لـ x تربيع

مثال 3: مشتقة قاطع التمام المكعب للدالة الأسية

حل مسائل مشتق قاطع التمام

إثبات صيغة مشتق قاطع التمام

اترك تعليقاً إلغاء الرد