مشتق أركسين

نشرح في هذه المقالة كيفية اشتقاق قوس جيب الزاوية للدالة. ستجد أمثلة على مشتقات قوس جيب الدوال ويمكنك أيضًا التدرب على التمارين التي تم حلها خطوة بخطوة. وأخيرًا، ستشاهد أيضًا عرضًا توضيحيًا لصيغة مشتقة أركسين.

ما هو مشتق أركسين؟

مشتق قوس الجيب لـ x هو واحد على الجذر التربيعي لواحد ناقص x تربيع.

$f(x)=\text{arcsen}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{\sqrt{1-x^2}}$

وبالتالي، فإن مشتقة قوس جيب الزاوية للدالة يساوي حاصل قسمة مشتقة تلك الدالة على الجذر التربيعي لواحد ناقص الدالة التربيعية.

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

منطقيا، يتم الحصول على الصيغة الثانية من خلال تطبيق قاعدة السلسلة على الصيغة الأولى.

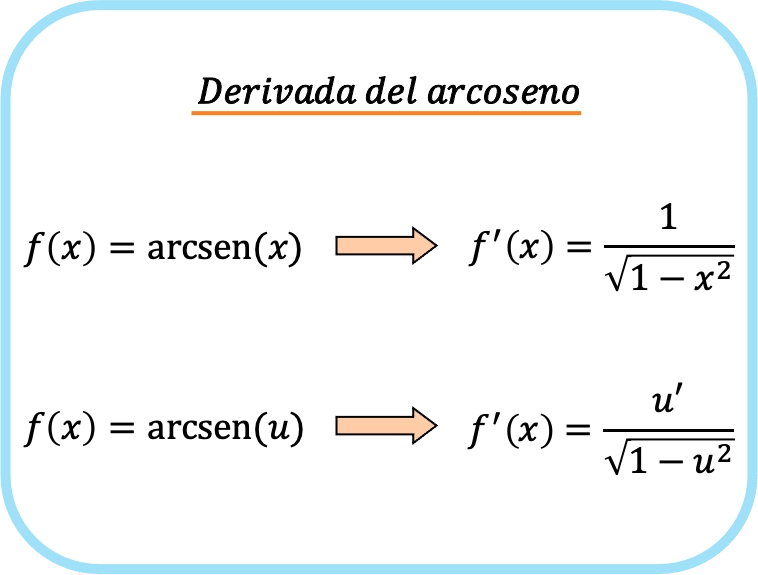
تذكر أن أركسين هي دالة عكسية للجيب، ولهذا السبب تسمى أيضًا جيب الجيب العكسي.

أمثلة على مشتق أركسين

بعد الاطلاع على صيغة مشتقة أركسين، سنشرح عدة أمثلة لهذا النوع من المشتقات المثلثية. بهذه الطريقة سيكون من الأسهل عليك فهم كيفية اشتقاق قوس جيب الزاوية للدالة.

مثال 1: مشتق قوس جيب الجيب لـ 2x

$f(x)=\text{arcsen}(2x)$

للعثور على مشتق دالة أركسين، نحتاج إلى استخدام الصيغة المقابلة لها:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

إذن مشتق 2x هو 2، وبالتالي فإن مشتق قوس جيب الجيب 2x هو 2 مقسومًا على جذر واحد ناقص 2x تربيع:

$f(x)=\text{arcsen}(2x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2}{\sqrt{1-(2x)^2}}=\cfrac{2}{\sqrt{1-4x^2}}$

مثال 2: مشتق قوس جيب التمام لـ x تربيع

$f(x)=\text{arcsen}(x^2)$

نستخدم صيغة مشتق أركسين لاشتقاقها:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

الدالة x ² هي من الدرجة الثانية، لذا فإن مشتقتها هي 2x. وبالتالي، فإن مشتق قوس جيب الجيب لـ x مرفوعًا للقوة 2 هو:

$f(x)=\text{arcsen}(x^2) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{2x}{\sqrt{1-\left(x^2\right)^2}}=\cfrac{2x}{\sqrt{1-x^4}}$

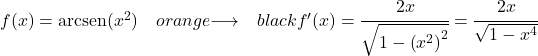
مثال 3: مشتق قوس جيب e ^x

$f(x)=\text{arcsen}(e^x)$

الدالة في هذا المثال هي دالة مركبة، لذا نحتاج إلى تطبيق قاعدة السلسلة لحل المشتقة:

$f(x)=\text{arcsen}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{\sqrt{1-u^2}}$

مشتق e ^x هو نفسه، وبالتالي فإن مشتق الدالة بأكملها هو:

$f(x)=\text{arcsen}(e^x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{e^x}{\sqrt{1-\left(e^x\right)^2}}=\cfrac{e^x}{\sqrt{1-e^{2x}}}$

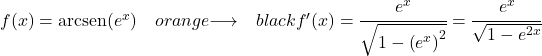
حل مسائل مشتق أركسين

استنتج دوال arcsine التالية:

$\text{A) }f(x)=\text{arcsen}(6x)$

$\text{B) }f(x)=\text{arcsen}(x^2-4x)$

$\text{C) }f(x)=\text{arcsen}\left(3x^4-6x^3+9+e^{x^2}\right)$

$\text{D) }f(x)=\text{arcsen}\left(\log_5(3x)\right)$

$\text{E) }f(x)=\text{arcsen}\left(\sqrt{4x}\right)$

انظر الحل

$\text{A) }f'(x)=\cfrac{6}{\sqrt{1-(6x)^2}}=\cfrac{6}{\sqrt{1-36x^2}}$

$\text{B) }f'(x)=\cfrac{2x-4}{\sqrt{1-(x^2-4x)^2}}$

$\text{C) }f'(x)=\cfrac{12x^3-18x^2+2x\cdot e^{x^2}}{\sqrt{1-(3x^4-6x^3+9+e^{x^2})^2}}$

$\text{D) }f'(x)=\cfrac{1}{\sqrt{1-\left(\log_5(3x)\right)^2}}\cdot \cfrac{3}{3x\cdot \ln 5}=\cfrac{1}{x\cdot \ln 5\cdot \sqrt{1-\left(\log_5(3x)\right)^2}}$

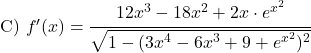
$\begin{aligned}\text{E) } f'(x)& =\cfrac{1}{\sqrt{1-\left(\sqrt{4x}\right)^2}}\cdot \cfrac{4}{2\sqrt{4x}}\\[1.5ex] &=\cfrac{2}{\sqrt{1-4x}\cdot 2\sqrt{x}}\\[1.5ex] &=\cfrac{1}{\sqrt{x-4x^2}} \end{aligned}$