▷ مشتق ظل التمام (الصيغة والأمثلة)

في هذه المقالة، سنرى كيفية استنتاج ظل التمام للدالة. ستجد أمثلة على مشتقات ظل التمام وحتى التمارين التي تم حلها خطوة بخطوة. وأخيرًا، نثبت صيغة مشتقة ظل التمام.

صيغة مشتقة ظل التمام

مشتق ظل التمام لـ x يساوي سالب واحد على مربع جيب التمام لـ x. مشتق ظل التمام لـ x يساوي أيضًا ناقص مربع قاطع التمام لـ x، وناقص مجموع واحد زائد مربع ظل التمام لـ x.

$\begin{array}{c}f(x)=\text{cotg}(x)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{1}{\text{sen}^2(x)}=-\text{cosec}^2(x)=-\left(1+\text{cotg}^2(x)\right)\end{array}$

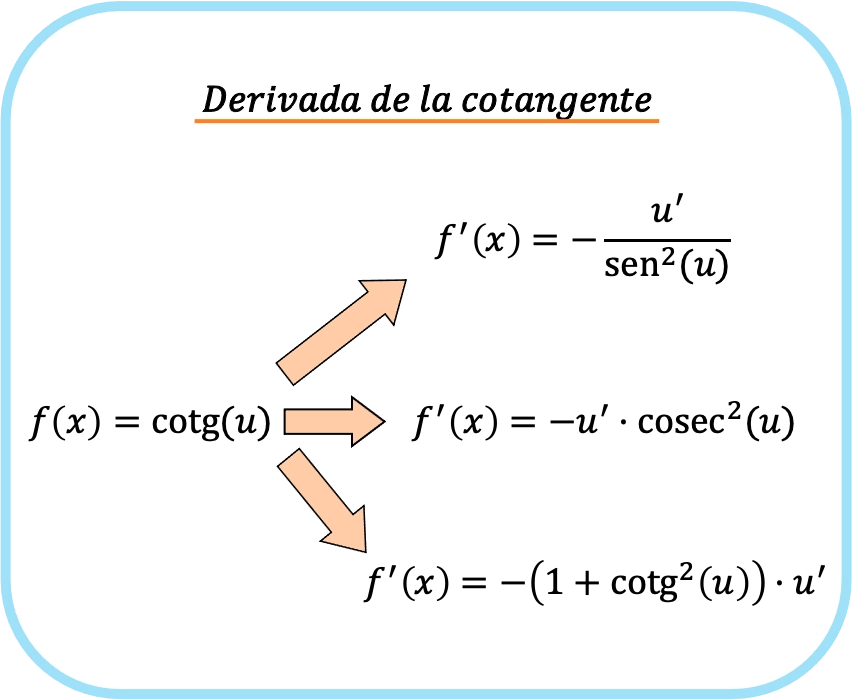
إذا كانت وسيطة ظل التمام دالة أخرى غير x، فإن صيغ مشتق ظل التمام للدالة هي نفس الصيغ السابقة، ولكن بضرب التعبيرات في مشتقة دالة الوسيطة.

$\begin{array}{c}f(x)=\text{cotg}(u)\\[1.5ex]\color{orange}\bm{\downarrow}\color{black}\\ f'(x)=-\cfrac{u'}{\text{sen}^2(u)}=-u' \cdot \text{cosec}^2(u)=-u' \cdot \left(1+\text{cotg}^2(u)\right)\end{array}$

هذا يعني أن هناك ثلاث صيغ مختلفة لإيجاد مشتقة ظل التمام. لكن، منطقياً، ليس من الضروري استخدام الصيغ الثلاثة جميعها، ولكن يمكنك اشتقاقها بالصيغة التي تفضلها.

أمثلة على مشتقات ظل التمام

الآن بعد أن رأينا صيغة مشتقة ظل تمام الدالة، سنحل في هذا القسم عدة أمثلة لهذا النوع من المشتقات المثلثية.

مثال 1: مشتقة ظل التمام 2x

في هذا المثال، سنرى ما هي مشتقة ظل التمام للدالة 2x.

$f(x)=\text{cotg}(2x)$

كما رأينا، لحساب مشتقة ظل التمام، يمكنك استخدام إحدى الصيغ الثلاث الموضحة أعلاه. في هذه الحالة، سوف نستخدم الصيغة الجيبية:

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

بما أن 2x هو حد من الدرجة الأولى، فإن مشتقته هي 2. وبالتالي فإن مشتقة ظل التمام 2x هي سالب اثنين مقسومًا على مربع جيب الزاوية 2x:

$f(x)=\text{cotg}(2x)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2}{\text{sen}^2(2x)}$

مثال 2: مشتق ظل التمام لـ x تربيع

في المثال الثاني، سنحدد مشتقة ظل التمام لـ x تربيع.

$f(x)=\text{cotg}(x^2)$

في هذا المثال، دالة وسيطة ظل التمام ليست x، لذلك يجب علينا تطبيق قاعدة السلسلة للتمييز بين ظل التمام.

$f(x)=\text{cotg}(u)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{u'}{\text{sen}^2(u)}$

مشتقة x تربيع هي 2x، لذا فإن مشتقة ظل التمام لـ x ² هي:

$f(x)=\text{cotg}(x^2)\quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=-\cfrac{2x}{\text{sen}^2(x^2)}$

مثال 3: مشتقة ظل التمام مكعبة

وأخيرًا، سنجد ما مقدار مشتقة ظل التمام المكعب لدالة متعددة الحدود:

$f(x)=\text{cotg}^3(x^5-6x^2+10)$

في هذه الحالة لدينا تركيبة من الدوال، لذلك نحتاج إلى استخدام قاعدة السلسلة مع صيغة مشتقة القوة لإيجاد مشتقة ظل التمام:

$\displaystyle f'(x)=-3\cdot\text{cotg}^2(x^5-6x^2+10)\cdot\frac{5x^4-12x}{\text{sen}^2(x^5-6x^2+10)}$

تمارين محلولة على مشتقة ظل التمام

احسب مشتقة دوال ظل التمام التالية:

$\text{A) } f(x)=\text{cotg}(5x)$

$\text{B) } f(x)=\text{cotg}(2x^4+10x-3)$

$\text{C) } \displaystyle f(x)=\text{cotg}^5\left(\frac{x}{2}\right)$

$\text{D) } f(x)=\text{cotg}\left(e^{x^2}\right)$

$\text{E) } f(x)=\text{cotg}\bigl(\ln(x^2)\bigr)$

$\text{F) } f(x)=\text{cotg}\left(\sqrt{8x}\right)$

انظر الحل

$\text{A) } f'(x)=-\cfrac{5}{\text{sen}^2(5x)}$

$\text{B) } f'(x)=-\cfrac{8x+10}{\text{sen}^2(2x^4+10x-3)}$

$\text{C) } \displaystyle f'(x)=5\cdot \text{cotg}^4\left(\frac{x}{2}\right)\cdot \left(-\frac{1}{\text{sen}^2\left(\frac{x}{2}\right)}\right)\cdot \frac{1}{2}=-\frac{5\cdot \text{cotg}^4\left(\frac{x}{2}\right)}{2\cdot \text{sen}^2\left(\frac{x}{2}\right)}$

$\text{D) } f'(x)=-\cfrac{2x\cdot e^{x^2}}{\text{sen}^2(e^{x^2})}$

$\text{E) } f'(x)=-\cfrac{\cfrac{2x}{x^2}}{\text{sen}^2\bigl(\ln(x^2)\bigr)}=-\cfrac{2}{x\cdot\text{sen}^2\bigl(\ln(x^2)\bigr)}$

$\text{F) } f'(x)=-\cfrac{\frac{8}{2\sqrt{8x}}}{\text{sen}^2\left(\sqrt{8x}\right)}=-\cfrac{4}{\sqrt{8x}\cdot \text{sen}^2\left(\sqrt{8x}\right)}$

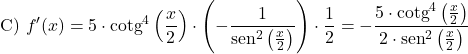
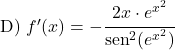
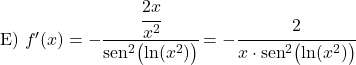
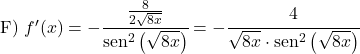
إثبات مشتقة ظل التمام

في هذا القسم الأخير، سنوضح صيغة مشتقة ظل التمام. للقيام بذلك، سنبدأ من التعريف الرياضي لدالة ظل التمام، والتي تساوي جيب التمام مقسومًا على الجيب:

$\text{cotg}(x)=\cfrac{\text{cos}(x)}{\text{sen}(x)}$

الآن نحن نشتق الدالة من خلال تطبيق قاعدة مشتقة خارج القسمة؛

$\displaystyle\bigl(\text{cotg}(x)\bigr)'=\left(\frac{\text{cos}(x)}{\text{sen}(x)}\right)'$

$\text{cotg}'(x)=\cfrac{-\text{sen}(x)\cdot \text{sen}(x)-\text{cos}(x)\cdot \text{cos}(x) }{\text{sen}^2(x)}$

$\text{cotg}'(x)=\cfrac{-\text{sen}^2(x)-\text{cos}^2(x)}{\text{sen}^2(x)}$

نأخذ العامل المشترك في المقام ونزيل إشارة السالب من الكسر:

$\text{cotg}'(x)=\cfrac{-\bigl(\text{sen}^2(x)+\text{cos}^2(x)\bigr)}{\text{sen}^2(x)}$

$\text{cotg}'(x)=-\cfrac{\text{sen}^2(x)+\text{cos}^2(x)}{\text{sen}^2(x)}$

ومن ناحية أخرى، نعلم أن مربع جيب الجيب بالإضافة إلى مربع جيب التمام يساوي واحدًا بفضل المتطابقة المثلثية الأساسية.

$\text{sen}^2(x)+\text{cos}^2(x)=1$

$\text{cotg}'(x)=-\cfrac{1}{\text{sen}^2(x)}$

وبذلك حصلنا على الصيغة الأولى لمشتقة ظل التمام. وبالمثل، فإن قاطع التمام هو المعكوس الضربي للجيب، لذلك تم أيضًا إثبات القاعدة الثانية لمشتقة ظل التمام:

$\text{cotg}'(x)=-\text{sec}^2(x)$

وأخيرًا، يمكن إثبات الصيغة الثالثة لمشتقة هذه الدالة المثلثية عن طريق تحويل الكسر من الخطوة السابقة إلى مجموع الكسور: