ما هو التخصيم متعدد الحدود؟ إنها تقنية رياضية تسمح لك بتحليل كثير الحدود إلى عوامل أو تعبيرات أبسط. وبفضل هذا التبسيط، سنكون قادرين على إجراء العمليات بين عدة تعبيرات جبرية بسهولة وراحة أكبر. لذلك، خلال هذه المقالة، سنناقش الطرق المختلفة لتحليل كثيرات الحدود وجميع حالات التحليل المحتملة.
كيفية تحليل كثير الحدود؟
هناك العديد من طرق التحليل التي لها بنية الحل الخاصة بها، ولكنها تعتمد في النهاية على نفس الشيء. بالإضافة إلى ذلك، يمكنك أيضًا العثور على مجموعة واسعة من الحالات المتعلقة بتكوين كثيرات الحدود. ولهذا السبب سنناقش في الأقسام التالية كافة الإجراءات الموجودة ومتى يتم استخدام كل منها. وأخيرا، سوف نطبق ذلك على مثال حقيقي حتى تنتهي من اكتساب المفاهيم.
عامل كثير الحدود بقاعدة روفيني
الطريقة الأكثر استخدامًا لتحليل كثيرات الحدود هي قاعدة روفيني ، لأنها سهلة الاستخدام ويمكن العثور على النتيجة بسرعة. الشيء الطبيعي هو استخدام هذه التقنية لتحليل كثيرات الحدود من الدرجة الأكبر من اثنين، أو حتى في بعض الأحيان لتحليل كثيرات الحدود من الدرجة الثانية. لأنه يسمح لك بالحصول على جذور كثير الحدود هذا بيانياً للغاية. على الرغم من أنه سيتم شرح هذا الاستخدام في القسم التالي الذي يركز على جذور التعبير الرياضي من هذا النوع.
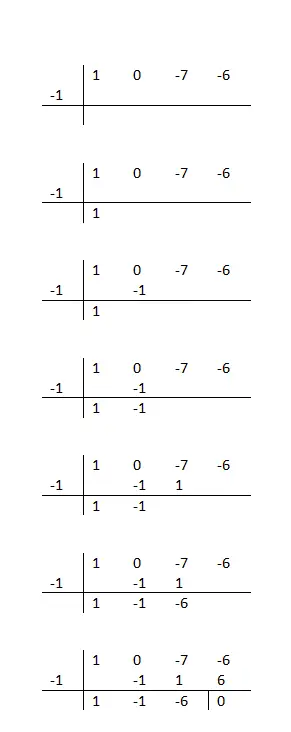
كيفية عمل Ruffini لتحليل كثيرات الحدود؟
في الأساس، سيتعين علينا كتابة معاملات المقسوم على خط أفقي وقيمة الجذر المحتمل لكثيرة الحدود في الجانب. نقول ممكن، لأنه سيتعين علينا البحث عن المقسوم عليه الذي يتيح لنا الحصول على باقي يساوي صفرًا. وإلا فإن هذا الرقم لن يكون جذرًا صالحًا وسيتعين عليك الاستمرار في المحاولة.
كنصيحة، نوصي بتجربة أرقام المقسوم عليها للمصطلح المستقل (القيمة الأخيرة للخط الأفقي فقط). لذا، لمعرفة ما إذا كان الرقم الذي اخترته صحيحًا، ما عليك سوى اتباع التسلسل الحسابي التالي:
تقوم بتقليل المعامل، وضربه في الجذر الذي تختبره، ثم كتابته أسفل المعامل التالي، ثم إجراء عملية جمع رأسي. كل ما عليك فعله هو تكرار هذه الخطوات حتى النهاية، وبمجرد الانتهاء ستعرف ما إذا كانت هذه القيمة صحيحة أم لا. نظرًا لأن الأرقام التي تعطي صفرًا فقط ستكون صالحة.
إذا لم يكن الإجراء الرياضي الذي يتعين عليك اتباعه واضحًا جدًا بالنسبة لك، فيمكنك إلقاء نظرة على المثال الموجود في العمود الموجود على يسار هذا النص. نوصي أيضًا بمحاولة تحليل كثيرة الحدود التالية إلى عوامل: x³ + 2x² – x – 2 (استنادًا إلى المثال). وأخيرًا، لمعرفة ما إذا كنت قد قمت بحل التمرين بشكل صحيح أم لا، يمكنك مقارنة نتيجتك بهذه النتيجة:
- التعبير الزائد = x² + 3x + 2
- الباقي = 0
وسنقوم الآن بتقديم شرح مختصر عن تطبيق روفيني في التحليل . على الرغم من أنك إذا كنت تريد معرفة كيفية استخدام هذا المورد الرياضي بالتفصيل، فإننا نوصي بالوصول إلى المقالة الأخيرة التي قمنا بربطها، حيث تم شرح كل شيء جيدًا هناك. ومع ذلك، فلنبدأ بشرح كيفية تحليل كثيرات الحدود إلى عوامل مع قاعدة روفيني:
- نرسم الشبكة: كما نرى في الصورة أعلاه، سنقوم بإنشاء صندوق نصنع فيه الروفيني. في الأساس، عليك أن تكتب معاملات التعبير مرتبة أفقيًا دون ترك تلك التي لها قيمة صفر. في النهاية، يجب أن يكون لديك تمثيل مشابه لتلك الموجودة في الصورة ولكن مع قيم كثيرة الحدود الخاصة بك.
- نقوم بحساب الجذور: بمجرد رسم البنية والتأكد من كتابة جميع الأرقام بشكل صحيح، سنبدأ في حساب الجذر. سوف تحتاج إلى العثور على الجذور باتباع تسلسل الحساب الذي تحدثنا عنه أعلى هذه القائمة مباشرةً (مع الصور).
- نعبر عن الجذر بالصورة (x – a): عندما يكون لدينا جميع جذور كثيرة الحدود فيجب أن نعبر عنها بالصورة التالية (x – a). مع الأخذ في الاعتبار أن a هي القيم التي حصلنا عليها، فمثلاً إذا استخرجنا النتيجة x = 2 و x = -2 و x = 4 فإننا سنحصل على (x – 2) و(x + 2) و( س – 4).
- نحن نجمع كل العوامل في تعبير واحد: أخيرًا، عندما يكون لدينا بالفعل جميع الجذور المعبر عنها بالتنسيق الصحيح، سيتعين علينا فقط جمعها في تعبير جبري واحد. بالاستمرار في المثال السابق، سيكون لدينا شيء مثل هذا: (x – 2) · (x + 2) · (x – 4).
إلى عوامل كثيرة الحدود باستخدام جذور كثيرة الحدود
لقد شرحنا نصف المفهوم الجذري لكثيرة الحدود في قسم روفيني. لكن التعريف الدقيق سيكون: جذر كثير الحدود P(x) هو قيمة عددية a، بحيث P(a) = 0 . وبالتالي فهو رقم قادر على إلغاء الدالة أو كثيرة الحدود المعنية. باختصار، يمكننا القول أنه يتم استخدامه لتحليل كثيرة الحدود إلى حاصل ضرب العوامل.
على سبيل المثال، إذا حصلنا على التعبير التالي x² − x − 2 وقمنا بتحليله إما باستخدام قاعدة روفيني أو ببساطة عن طريق حل المعادلة التربيعية x² − x − 2 = 0. سنحصل على قيمتين x = -1 و x = 2، لذا إذا قمنا بتغييرها إلى الصيغة (x – a) وجمعناها معًا، فسنصل إلى التعبير التالي: (x + 1) (x − 2)، أي كثيرة الحدود المحللة . ويمكننا تطبيق ذلك على كثيرات الحدود ذات الدرجة الأكبر من اثنين، على الرغم من أن التعبير يتكون من أكثر من حد واحد.
تحليل كثير الحدود عن طريق استخراج العامل المشترك
عندما نريد تحليل كثيرات الحدود دون وجود حد مستقل أو تعبيرات لها عامل مشترك في جميع الحدود، فيمكننا تبسيط كثيرة الحدود باستخدام هذه التقنية. إنها تتضمن بشكل أساسي تطبيق خاصية التوزيع على التعبير بأكمله، وإزالة العامل المشترك المتكرر وإضافته عن طريق ضرب كثير الحدود بالكامل. ستجد أدناه مثالاً للحالة الأولى التي تحدثنا عنها (كثيرة الحدود بدون مصطلح مستقل):
2x³ + 10x² – 6x = 2x (x² + 5x – 3)
استخراج مزدوج للعامل المشترك
يمكن أيضًا استخراج العوامل المشتركة عن طريق استخلاص عوامل أكثر تعقيدًا، والتي تتضمن متغيرات متعددة. ويمكنك حتى استخراج كثيرات الحدود المشتقة من التعبير الرئيسي نفسه. من المهم عدم وضع حدود عندما تريد إجراء هذا النوع من العمليات، لأن الهدف من استخلاص العوامل هو تبسيط التعبير الجبري قدر الإمكان .
تحليل كثيرات الحدود باستخدام الهويات البارزة
يمكن أن تساعدنا المنتجات البارزة في تحليل التعبيرات كثيرة الحدود، لأنها نوع من التعبيرات الجبرية المبسطة. ومن ثم فهي تساعدنا على الانتقال مباشرة من كثيرة الحدود الطويلة إلى صيغة صغيرة تتكون من بضعة حدود. ولذلك يوصى بشدة بتعلم صيغ الهويات البارزة لتتمكن من تحديد متى يمكنك استخدامها بسرعة. وبالتالي توفير الوقت في التخصيم باستخدام Ruffini أو أي من الطرق الأخرى. بعد ذلك، سنغطي القواعد الثلاثة التي تحتاج إلى تعلمها:
- فرق المربعات: أ² – ب² = (أ + ب) · (أ – ب)
- مربع المجموع: أ² + 2أ + ب² = (أ + ب)²
- مربع الطرح: أ² – 2أ ب + ب² = (أ – ب)²
تحليل كثيرات الحدود عن طريق التجميع
في بعض الحالات يمكننا العثور على كثيرة الحدود ذات البنية x² – ax – bx + ab والتي يمكن تبسيطها عن طريق إزالة العامل المشترك: x (x – a) – b (x – a). وإذا أخذنا العامل المشترك مرة أخرى، فيمكن تبسيطه أكثر: (x – a) · (x – b). لذلك، فإن جذور كثيرة الحدود هذه ستكون x = a و x = b. كما ترى، هذا النوع من التعبيرات الجبرية له بنية سهلة التحليل والاستخدام.
تمارين تحليل كثيرات الحدود
وأخيرًا، نريد أن نقدم لك سلسلة من التمارين حتى تتمكن من التدرب على تحليل كثيرات الحدود إلى عواملها. بهذه الطريقة ستتمكن من استيعاب النظرية التي شرحناها اليوم بشكل أفضل. ببساطة، عليك حل التمارين الموجودة في دفترك ثم مقارنة النتائج مع تلك التي نقدمها لك أدناه.
- س 4 -1 = (س 2 + 1) (س + 1) (س – 1)
- س 5 + س 4 – س – 1 = (س – 1) (س + 1) 2 (س 2 + 1)
- 9×2 + 30س + 25 = (3س + 5) 2
- س 4 – 3س 3 – 3س 2 + 11س – 6 = (س + 2) (س – 3) (س – 1) 2