قوى المصفوفة -

في هذه الصفحة سنرى كيفية حساب قوى المصفوفات. ستجد أيضًا أمثلة وتمارين تم حلها خطوة بخطوة لقوى المصفوفات والتي ستساعدك على فهمها بشكل مثالي. سوف تتعلم أيضًا ما هي القوة n للمصفوفة وكيفية العثور عليها.

كيف يتم حساب قوة المصفوفة؟

لحساب قوة المصفوفة ، يجب عليك ضرب المصفوفة في نفسها عدة مرات كما يقول الأس. على سبيل المثال:

$A^4 = A \cdot A \cdot A \cdot A$

لذلك، للحصول على قوة المصفوفة، عليك أن تعرف كيفية حل ضرب المصفوفات . وإلا فلن تتمكن من حساب مصفوفة الطاقة.

مثال لحساب قوة المصفوفة:

ولذلك، يتم حساب قوة المصفوفة التربيعية عن طريق ضرب المصفوفة في نفسها. وبالمثل، فإن المصفوفة المكعبة تساوي المصفوفة التربيعية للمصفوفة نفسها. وبالمثل، لإيجاد قوة مصفوفة مرفوعة إلى أربعة، يجب ضرب المصفوفة المرفوعة إلى ثلاثة في المصفوفة نفسها. وما إلى ذلك وهلم جرا.

هناك خاصية مهمة لقوة المصفوفة يجب أن تعرفها: لا يمكن حساب قوة المصفوفة إلا عندما تكون مربعة ، أي عندما تحتوي على نفس عدد الصفوف مثل الأعمدة.

ما هي قوة n للمصفوفة؟

القوة n للمصفوفة هي تعبير يسمح لنا بحساب أي قوة للمصفوفة بسهولة.

غالبًا ما تتبع قوى المصفوفات نمطًا ما . لذلك، إذا تمكنا من فك رموز التسلسل الذي تتبعه، فسنكون قادرين على حساب أي قوة دون الحاجة إلى إجراء جميع عمليات الضرب.

هذا يعني أنه يمكننا إيجاد صيغة تعطينا القوة النونية لمصفوفة دون الحاجة إلى حساب جميع القوى.

نصائح لاكتشاف النمط الذي تتبعه القوى:

تكافؤ الأس . ربما تكون حتى القوى في اتجاه والقوى الفردية في الاتجاه الآخر.
تباين العلامات. على سبيل المثال، يمكن أن تكون عناصر القوى الزوجية موجبة وعناصر القوى الفردية سالبة، أو العكس.
التكرار: هل تتكرر نفس المصفوفة كل عدد معين من القوى أم لا.
يجب علينا أيضًا أن ننظر إلى ما إذا كانت هناك علاقة بين الأس وعناصر المصفوفة.

مثال لحساب القدرة n للمصفوفة:

يكون
$A$

المصفوفة التالية، احسب

$A^n$

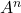
و

$A^{100}$

.

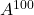
$\displaystyle A = \begin{pmatrix} 1 & 1 \\[1.1ex] 1 & 1 \end{pmatrix}$

سنقوم أولاً بحساب عدة قوى للمصفوفة

$A$

لمحاولة تخمين النمط الذي تتبعه القوى. لذلك نحن نحسب

$A^2$

$A^3$

$A^4$

$A^5:$

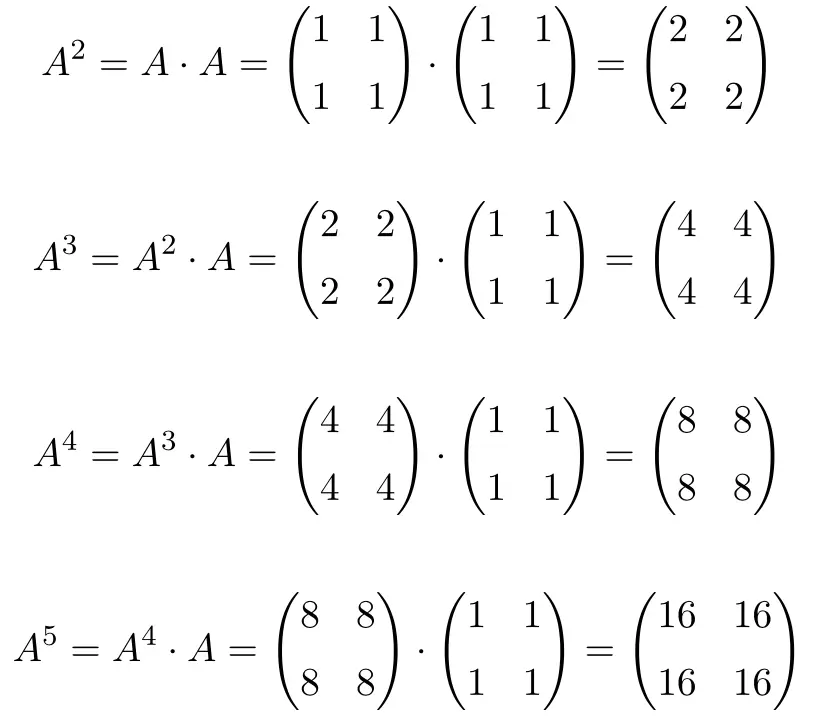
تمرين تم حله خطوة بخطوة لقوى المصفوفات 2×2

عند حساب ما يصل إلى

$A^5$

، نرى أن صلاحيات المصفوفة

$A$

وهي تتبع نمطًا: لكل زيادة في الأس، يتم ضرب النتيجة في 2. لذلك، جميع المصفوفات هي قوى للعدد 2:

$\displaystyle A^2= \begin{pmatrix} 2 & 2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 2^1 & 2^1 \\[1.1ex] 2^1 & 2^1 \end{pmatrix}$

$\displaystyle A^3= \begin{pmatrix} 4 & 4 \\[1.1ex] 4 & 4 \end{pmatrix}=\begin{pmatrix} 2^2 & 2^2 \\[1.1ex] 2^2 & 2^2 \end{pmatrix}$

$\displaystyle A^4= \begin{pmatrix} 8 & 8 \\[1.1ex] 8 & 8 \end{pmatrix}=\begin{pmatrix} 2^3 & 2^3 \\[1.1ex] 2^3 & 2^3 \end{pmatrix}$

$\displaystyle A^5= \begin{pmatrix} 16 & 16 \\[1.1ex] 16 & 16 \end{pmatrix}=\begin{pmatrix} 2^4 & 2^4 \\[1.1ex] 2^4 & 2^4 \end{pmatrix}$

يمكننا بالتالي استنتاج صيغة القوة النونية للمصفوفة

$A:$

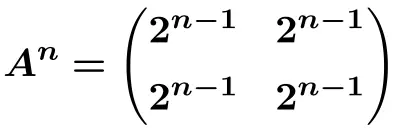
ومن هذه الصيغة يمكننا الحساب

$A^{100}:$

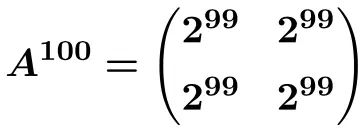
حل مشاكل قوة المصفوفة

التمرين 1

خذ بعين الاعتبار المصفوفة التالية ذات البعد 2×2:

$\displaystyle A=\begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix}$

احسب:

$\displaystyle A^4$

انظر الحل

لحساب قوة المصفوفة، عليك ضرب المصفوفة واحدة تلو الأخرى. ولذلك، فإننا نحسب أولا

$\displaystyle A^2 :$

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1\end{pmatrix}$

الآن نحسب

$\displaystyle A^3 :$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 4 \\[1.1ex] -2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} =\begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix}$

وأخيرا نحسب

$\displaystyle A^4 :$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} -5 & 2 \\[1.1ex] -1 & -5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 2 \\[1.1ex] -1 & 1 \end{pmatrix} = \begin{pmatrix} \bm{-7} & \bm{-8} \\[1.1ex] \bm{4} & \bm{-7} \end{pmatrix}$

تمرين 2

النظر في المصفوفة التالية من الترتيب 2:

$\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}$

احسب:

$\displaystyle A^{35}$

انظر الحل

$\displaystyle A^{35}$

إنها قوة كبيرة جدًا بحيث لا يمكن حسابها يدويًا، لذلك يجب أن تتبع قوى المصفوفة نمطًا ما. لذلك دعونا نحسب

$\displaystyle A^5$

لمحاولة فهم التسلسل الذي يتبعونه:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix} \cdot \begin{pmatrix}1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}$

بهذه الطريقة يمكننا أن نرى النمط الذي تتبعه القوى: عند كل قوة، تظل جميع الأرقام كما هي، باستثناء العنصر الموجود في العمود الثاني من الصف الثاني، والذي يتم ضربه بـ 3. لذلك، تظل جميع الأرقام كما هي دائمًا. والعنصر الأخير هو قوة 3:

$\displaystyle A=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^1 \end{pmatrix}$

$\displaystyle A^2=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 9 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^2 \end{pmatrix}$

$\displaystyle A^3=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 27 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^3 \end{pmatrix}$

$\displaystyle A^4=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 81 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^4 \end{pmatrix}$

$\displaystyle A^5=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 243 \end{pmatrix}=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^5 \end{pmatrix}$

إذن صيغة القوة النونية للمصفوفة

$\displaystyle A$

شرق:

$\displaystyle A^n=\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 3^n\end{pmatrix}$

ومن هذه الصيغة يمكننا الحساب

$\displaystyle A^{35}:$

$\displaystyle\bm{A^{35}=}\begin{pmatrix} \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{3^{35}}\end{pmatrix}$

التمرين 3

خذ بعين الاعتبار المصفوفة 3×3 التالية:

$\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

احسب:

$\displaystyle A^{100}$

انظر الحل

$\displaystyle A^{100}$

إنها قوة كبيرة جدًا بحيث لا يمكن حسابها يدويًا، لذلك يجب أن تتبع قوى المصفوفة نمطًا ما. لذلك دعونا نحسب

$\displaystyle A^5$

لمحاولة فهم التسلسل الذي يتبعونه:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1\end{pmatrix} \cdot \begin{pmatrix}1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

بهذه الطريقة يمكننا أن نرى النمط الذي تتبعه القوى: عند كل قوة، تظل جميع الأرقام كما هي، باستثناء الكسور، التي تزيد بمقدار واحد في البسط:

$\displaystyle A=\begin{pmatrix} 1 & \frac{1}{5} & \frac{1}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^2= \begin{pmatrix} 1 & \frac{2}{5} & \frac{2}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^3= \begin{pmatrix} 1 & \frac{3}{5} & \frac{3}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= \begin{pmatrix} 1 & \frac{4}{5} & \frac{4}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^5= \begin{pmatrix} 1 & \frac{5}{5} & \frac{5}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

إذن صيغة قوة المصفوفة n

$\displaystyle A$

شرق:

$\displaystyle A^n= \begin{pmatrix} 1 & \frac{n}{5} & \frac{n}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

ومن هذه الصيغة يمكننا الحساب

$\displaystyle A^{100}:$

$\displaystyle A^{100}= \begin{pmatrix} 1 & \frac{100}{5} & \frac{100}{5} \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} \bm{1} & \bm{20} & \bm{20} \\[1.1ex] \bm{0} & \bm{1} & \bm{0} \\[1.1ex] \bm{0} & \bm{0} & \bm{1} \end{pmatrix}$

التمرين 4

خذ بعين الاعتبار المصفوفة التالية ذات الحجم 2×2:

$\displaystyle A=\begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}$

احسب:

$\displaystyle A^{201}$

انظر الحل

$\displaystyle A^{201}$

إنها قوة كبيرة جدًا بحيث لا يمكن حسابها يدويًا، لذلك يجب أن تتبع قوى المصفوفة نمطًا ما. في هذه الحالة، لا بد من حساب

$\displaystyle A^{8}$

لمعرفة التسلسل الذي يتبعونه:

$\displaystyle A^2= A \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1\end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix}$

$\displaystyle A^6= A^5 \cdot A = \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

$\displaystyle A^7= A^6 \cdot A = \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix}$

$\displaystyle A^8= A^7 \cdot A = \begin{pmatrix}0 & 1 \\[1.1ex] -1 & 0 \end{pmatrix} \cdot \begin{pmatrix} 0 & -1 \\[1.1ex] 1 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \bm{I}$

بهذه الحسابات يمكننا أن نرى أن كل 4 قوى نحصل عليها مصفوفة الهوية. وهذا يعني أنه سيعطينا نتيجة لذلك مصفوفة هوية القوى

$\displaystyle A^4$

$\displaystyle A^8$

$\displaystyle A^{12}$

$\displaystyle A^{16}$

،… لذا احسب

$\displaystyle A^{201}$

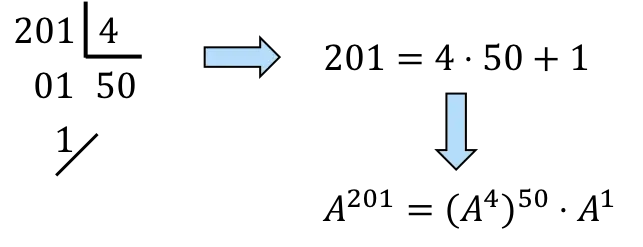
يجب علينا تحليل 201 إلى مضاعفات 4:

تمرين تم حله خطوة بخطوة لقوى المصفوفات 2x2 والقوة n

$\displaystyle 201= 4 \cdot 50 +1$

،حتى الآن،

$A^{201}$

سيكون 50 مرة

$\displaystyle A^{4}$

و لمرة واحدة

$\displaystyle A^{1}:$

$\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1$

وكيف نعرف ذلك

$\displaystyle A^4$

هي مصفوفة الهوية

$\displaystyle I :$

$\displaystyle A^4 =I$

$\displaystyle A^{201}=\left(A^4 \right)^{50} \cdot A^1 = I^{50}\cdot A$

علاوة على ذلك، فإن مصفوفة الهوية المرفوعة إلى أي رقم تعطي مصفوفة الهوية. حتى الآن:

$\displaystyle A^{201}= I^{50}\cdot A = I \cdot A$

وأخيرًا، أي مصفوفة مضروبة في مصفوفة الهوية تعطي المصفوفة نفسها. لذا:

$\displaystyle A^{201}= I \cdot A = A$

لماذا

$A^{201}$

مساوي ل

$A:$

$\displaystyle A^{201}= A =\begin{pmatrix} \bm{0} & \bm{-1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

التمرين 5

خذ بعين الاعتبار المصفوفة التالية من الترتيب 3:

$\displaystyle A=\begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}$

احسب:

$\displaystyle A^{62}$

انظر الحل

من الواضح، حساب قوة المصفوفة

$\displaystyle A^{62}$

هذه عملية حسابية كبيرة جدًا بحيث لا يمكن إجراؤها يدويًا، لذا يجب أن تتبع قوى المصفوفة نمطًا ما. في هذه الحالة، لا بد من حساب

$\displaystyle A^{6}$

لمعرفة التسلسل الذي يتبعونه:

$\displaystyle A^2= A \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}$

$\displaystyle A^3= A^2 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\displaystyle A^4= A^3 \cdot A = \begin{pmatrix}1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix}$

$\displaystyle A^5= A^4 \cdot A = \begin{pmatrix}3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1 \end{pmatrix}$

$\displaystyle A^6= A^5 \cdot A = \begin{pmatrix}3 & 3 & 1 \\[1.1ex] -2 & -2 & -1 \\[1.1ex] 0 & 1 & -1\end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & -3 & 1 \\[1.1ex] -2 & -3 & 0 \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

بهذه الحسابات يمكننا أن نرى أن كل 3 قوى نحصل على مصفوفة الهوية. وهذا يعني أنه سيعطينا نتيجة لذلك مصفوفة هوية القوى

$\displaystyle A^3$

$\displaystyle A^6$

$\displaystyle A^{9}$

$\displaystyle A^{12}$

،… لكي تحسب

$\displaystyle A^{62}$

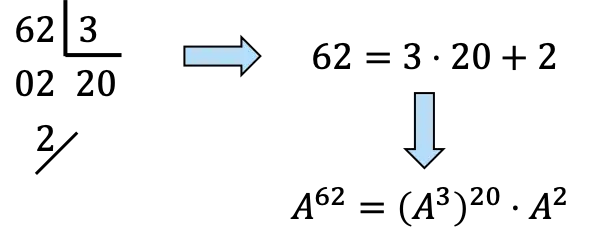
يجب علينا تحليل 62 إلى مضاعفات 3:

تمرين تم حله خطوة بخطوة لقوة مصفوفة 3x3، القوة n

$\displaystyle 62= 3 \cdot 20 +2$

،حتى الآن،

$\displaystyle A^{62}$

سيكون 20 مرة

$\displaystyle A^{3}$

و لمرة واحدة

$\displaystyle A^{2}:$

$\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2$

وكيف نعرف ذلك

$\displaystyle A^3$

هي مصفوفة الهوية

$\displaystyle I :$

$\displaystyle A^3 =I$

$\displaystyle A^{62}=\left(A^3 \right)^{20} \cdot A^2 = I^{20}\cdot A^2$

علاوة على ذلك، فإن مصفوفة الهوية المرفوعة إلى أي رقم تعطي مصفوفة الهوية. حتى الآن:

$\displaystyle A^{62}= I^{20}\cdot A^2 = I \cdot A^2$

وأخيرًا، أي مصفوفة مضروبة في مصفوفة الهوية تعطي نفس المصفوفة. حتى الآن:

$\displaystyle A^{62}= I \cdot A^2 = A^2$

لماذا

$A^{62}$

سيكون مساويا ل

$A^{2}$

والتي قمنا بحساب النتيجة لها سابقًا:

$\displaystyle A^{62}= A^2=\begin{pmatrix} \bm{3} & \bm{3} & \bm{1} \\[1.1ex] \bm{-2} & \bm{-2} & \bm{-1} \\[1.1ex] \bm{0} & \bm{1} & \bm{-1} \end{pmatrix}$

إذا كانت هذه التمارين المتعلقة بقوى المصفوفات المربعة مفيدة لك، فيمكنك أيضًا العثور على تمارين محلولة خطوة بخطوة حول جمع وطرح المصفوفات ، وهي إحدى العمليات الأكثر استخدامًا مع المصفوفات.

كيف يتم حساب قوة المصفوفة؟

مثال لحساب قوة المصفوفة:

ما هي قوة n للمصفوفة؟

مثال لحساب القدرة n للمصفوفة:

حل مشاكل قوة المصفوفة

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد