تسمح لنا قاعدة الثلاثة بمعرفة علاقات التناسب الموجودة بين قيم معينة. وبفضل هذا فإننا نطبقه يوميًا تقريبًا في أي مجال من مجالات الحياة اليومية. على سبيل المثال: حساب النسب المئوية ، وإجراء التحويلات بين الوحدات (الكتلة، والحجم، والوقت، وما إلى ذلك) وبشكل عام إجراء الحسابات على أساس المعادلات. هذا التطبيق الأخير هو الذي يسمح لنا باستخدام هذا المورد الرياضي في أي موضوع تقريبًا.
لذا، إذا كنت تريد معرفة كيفية حل قواعد الثلاثة ، فنوصيك بالبقاء حتى نهاية المقال. وسنشرح فيها كيفية حلها وما هي أنواعها وتطبيقاتها وستجد أيضًا بعض الأمثلة التي تم حلها. باختصار، بحلول الوقت الذي تنتهي فيه من قراءة هذا المقال، ستعرف كل ما يمكن معرفته حول هذا المفهوم الرياضي.
قاعدة الآلة الحاسبة الثلاثة
باستخدام هذه القواعد المكونة من ثلاث آلات حاسبة (الأولى هي التناسب المباشر والثانية هي التناسب غير المباشر)، ستتمكن من التحقق من جميع تمارينك وتصحيحها. تشغيله بسيط للغاية، كل ما عليك فعله هو إدخال البيانات التي تعرفها في ثلاثة من المربعات الأربعة وعندما تنقر على زر الحساب، سيتم عرض قيمة x. لكن لا تقلق إذا كنت لا تزال لا تعرف كيفية هيكلة عملية حسابية من هذا النوع، لأننا في القسم التالي سنشرحها لك بالتفصيل.
القاعدة المباشرة للآلة الحاسبة الثلاثة
عكس القاعدة من ثلاثة حاسبة
كيفية جعل قاعدة الثلاثة؟
لحل قاعدة الثلاثة، يجب عليك أولاً تحديد القاعدة التي ستستخدمها: قاعدة الثلاثة المباشرة أو قاعدة الثلاثة غير المباشرة. علينا أيضًا أن نميز نوع التناسب الذي سنستخدمه: قاعدة الثلاثة البسيطة أو قاعدة الثلاثة المركبة. وبما أن كل شخص لديه أحد هذه الخيارات، فإن لديه طريقة مختلفة لتنظيم البيانات وصيغة مختلفة . لذا، ولمعرفة متى تختار كل نوع، ننصحك بقراءة الشرح التالي حول كيفية حل قاعدة الثلاثة.
1. التعرف على العلاقات بين المتغيرات المختلفة
الخطوة الأولى لحل قاعدة الثلاثة هي عمل رسم بياني أو علاقة بين المتغيرات . بشكل عام، يتم ذلك عادةً باستخدام المخطط النموذجي الذي يمكن رؤيته في الصورة أدناه. بفضل هذا سيكون لدينا هيكل أوضح للحساب وبعد ذلك يمكننا إجراء العمليات الحسابية. تحتاج فقط إلى استبدال الحروف A وB وC بالقيم المقابلة: في العمود الأيسر ستنتقل القيم الرقمية للحجم الذي تعرفه ككل (كلا القيمتين) وفي العمود الأيمن ستنتقل القيم من القدر الذي له المجهول. تحتاج أيضًا إلى احترام الخطوط، لذلك يجب أن تكون A هي قيمة الحجم على اليسار المرتبطة بالمتغير B.
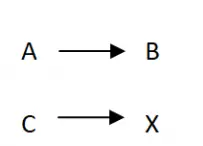
2. تحديد التناسب في قاعدة الثلاثة
ستكون الخطوة التالية هي تحديد التناسب بين المتغيرات، وسنفعل ذلك من خلال تحليل التغير في القيمة العددية بين المتغيرات لكل حجم. إذا انتهى بنا الأمر إلى قاعدة الثلاثة المستقيمة، فعندما تزيد إحدى الكميتين، ستزداد الأخرى أيضًا. لكن إذا انتهى بنا الأمر إلى قاعدة عكسية للثلاثة، فعندما تزيد كمية واحدة، تقل الكمية الأخرى. من المهم أن نأخذ ذلك في الاعتبار، حيث أن الصيغة ستختلف من حالة إلى أخرى.
3. قواعد بسيطة أو مكونة من ثلاثة
وأخيرًا، سنفرق قواعد الثلاثة إلى نوعين، اعتمادًا على عدد المتغيرات التي نربطها باستخدام التناسب. وفي حالة قاعدة الثلاثة البسيطة، نحصل على قيمة المتغير X من تناسب كمية أخرى. بينما تسمح لنا القاعدة المكونة من ثلاثة بحساب المتغير X، على أساس التناسب بين كميتين أو أكثر. بعد ذلك، سوف نعرض لك الصيغ والتمثيل البياني لهذين المفهومين، حتى لا يكون هناك شك في ذلك:

مثال على قاعدة بسيطة من ثلاثة
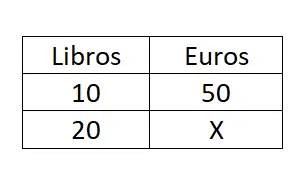
إذا كانت تكلفة عشرة كتب خمسين يورو، فإذا اشترينا 20 كتابًا، فكم سننفق من المال؟
للحصول على النتيجة، علينا حل قاعدة بسيطة ومباشرة من ثلاثة. لذلك سوف نستخدم الصيغة X = (B · C) / A:
مثال على قاعدة مكونة من ثلاثة
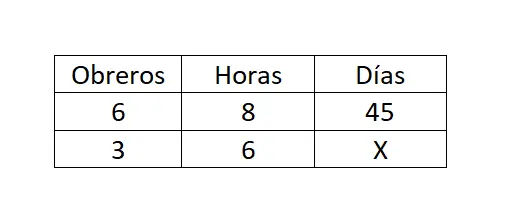
إذا كان 6 عمال يعملون 8 ساعات يوميًا يقومون ببناء منزل في 45 يومًا، فكم يومًا سيستغرق 3 عمال يعملون 6 ساعات يوميًا لإكمال نفس البناء؟
في هذه الحالة لدينا قاعدة مركبة وغير مباشرة وهي ثلاثة. ولذلك، سوف نستخدم الصيغة X = (أ 1 · ب 1 · ج 1 ) / (أ 2 · ب 2 ):
تطبيقات على قاعدة الثلاثة
كما علقنا في المقدمة، فإن قواعد الثلاثة تسمح لنا بحساب أشياء كثيرة، وبالتالي، فإننا نطبقها في أي مجال من مجالات الحياة اليومية. وعلى الرغم من أن هذا النوع من التطبيقات له خاصية مشتركة، إلا أنه يتم حسابه باستخدام النسب . لإعطاء بعض الأمثلة:
- حساب النسب المئوية
- التحويلات بين الوحدات
- حساب جرعات الدواء
- حساب العمولات
- حساب الدرجات
وفي الواقع تقريبا جميع العمليات التي تتطلب التكافؤ أو ما شابه.
القاعدة الثالثة في الآلة الحاسبة العلمية
في الآلات الحاسبة العلمية الأكثر شيوعًا، لا توجد عادةً وظيفة أو مفتاح يسمح لنا بحل قواعد العدد ثلاثة. لذا، إذا لم يكن لديك آلة حاسبة متقدمة ، يمكنك من خلالها إضافة وظائف مخصصة، فلن تكون قادرًا على حل قواعد الرقم 3. لذلك سيتعين عليك القيام بالعملية بشكل منفصل (على ورقة أو في رأسك) ثم قم بإجراء الجزء الحسابي في الآلة الحاسبة. في البداية قد يبدو الأمر بطيئًا بعض الشيء، ولكن عندما تتدرب وتكون قادرًا على تخيل قاعدة الثلاثة المرسومة في عقلك، فسوف تتمكن من حلها في ثانية واحدة .
أخيرًا، دعني أخبرك أنه إذا أردت مراجعة المزيد من قواعد التمارين الثلاثة، نترك لك رابط التمارين للتدرب عليها. ومع ذلك، نأمل أن تساعدك هذه المقالة وآلة حاسبة القاعدة الثالثة المتوفرة لدينا عبر الإنترنت على فهم هذا المفهوم الرياضي بشكل أفضل.