حساب الانحراف المركزي للقطع الناقص

ستجد في هذه الصفحة معنى انحراف القطع الناقص وكيفية حسابه (الصيغة). بالإضافة إلى ذلك، سترى أمثلة على حسابات الانحراف المركزي للقطع الناقص.

ما هو الانحراف المركزي للقطع الناقص؟

انحراف القطع الناقص هو معلمة تقيس مدى استدارة الشكل الناقص أو تسطيحه، أي أن انحراف الشكل الناقص يشير إلى مدى تشابه الشكل الناقص مع الدائرة.

من ناحية أخرى، دعونا نتذكر أيضًا مما يتكون القطع الناقص: القطع الناقص هو موضع جميع نقاط المستوى الذي يكون مجموع المسافات إلى نقطتين ثابتتين أخريين (تسمى البؤرتان F وF’) ثابتًا.

صيغة الانحراف البيضوي

بعد أن رأينا تعريف الانحراف المركزي للقطع الناقص، دعونا نرى كيف يتم حسابه من صيغته:

صيغة الانحراف المركزي للقطع الناقص هي كما يلي:

$e=\cfrac{c}{a}$

ذهب:

$e$

هو الانحراف من القطع الناقص
$c$

هي المسافة من بؤرة القطع الناقص (النقطتان F وF’) إلى مركزه
$a$

هو طول المحور شبه الرئيسي (أو الرئيسي) للقطع الناقص.

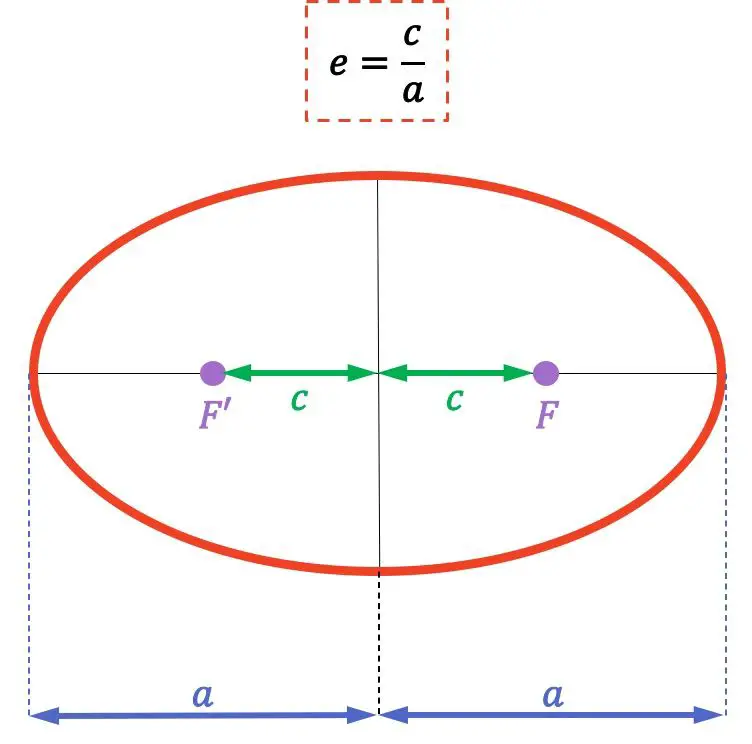
تذكر أن بؤرة الشكل الناقص هي النقاط الثابتة التي يكون مجموع مسافاتها إلى أي نقطة على الشكل الناقص ثابتًا. بالإضافة إلى ذلك، المسافة بين نقطتي التركيز تسمى البعد البؤري.

وتتراوح قيمة الانحراف من صفر، أي أنها دائرة كاملة، إلى واحد، أي أنها خط أفقي. من الواضح أنه لم يتم تضمين 0 و1 لأن الكائنات الهندسية الناتجة لم تعد عبارة عن علامات ناقصة.

$0 Par conséquent, comme vous pouvez le voir dans la représentation graphique ci-dessous, plus la valeur de l'excentricité de l'ellipse est petite, plus elle ressemble à un cercle, au contraire, plus le coefficient est grand, plus l'ellipse est aplatie. <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/excentricite-dellipse.webp" alt="valeur de l'excentricité de l'ellipse" class="wp-image-2095" width="669" height="154" srcset="" sizes=""></figure> </div> <p> En bref, l’excentricité d’une ellipse est un coefficient dont la valeur détermine la forme qu’elle a. </p> <div class="adsb30" style=" margin:12px; text-align:center"> <div id="ezoic-pub-ad-placeholder-109"></div> </div> <p> Si vous êtes plus intéressé par les caractéristiques d’une ellipse, vous pouvez vous référer à l’ <a href="https://mathority.org/equation-de-la-formule-de-l'ellipse/">équation de l’ellipse</a> . Sur cette page, vous trouverez une explication détaillée de ce qu’est une ellipse, de tous ses éléments et de la façon dont son équation est calculée. Et, en plus, vous pourrez voir plusieurs exemples, exercices et problèmes résolus sur des ellipses. </p> <h2 class="wp-block-heading"><span class="ez-toc-section" id="relacion-importante-para-hallar-la-excentricidad-de-la-elipse"></span> Relation importante pour trouver l’excentricité de l’ellipse<span class="ez-toc-section-end"></span></h2> <p> Les différents éléments d’une ellipse sont liés les uns aux autres. De plus, les relations entre eux sont très importantes pour les exercices sur les ellipses, car elles sont généralement nécessaires pour résoudre des problèmes sur les ellipses et déterminer leurs équations. Comme nous l’avons vu plus haut dans l’explication de la notion d’excentricité de l’ellipse, la distance de tout point de l’ellipse au foyer F plus la distance du même point au foyer F’ est constante. Eh bien, cette valeur constante est égale à deux fois ce que mesure le demi-grand axe. Autrement dit, l’égalité suivante vaut pour tout point d’une ellipse :” title=”Rendered by QuickLaTeX.com” height=”478″ width=”3899″ style=”vertical-align: -4px;”></p> <p> د(P,F) + د(P,F’)= 2أ</p> <p class=$ $Où$

د (ف، و)

$et$

د(ف، و’)

$est la distance du point P au foyer F et F' respectivement et$

لديه

$est la longueur de l'axe semi-focal. Par conséquent, puisque le sommet de l'axe secondaire est juste au milieu de l'axe principal, la distance de celui-ci à l'un des foyers est équivalente à la longueur du demi-axe principal ($

لديه

$): <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/relation-delements-dellipse.webp" alt="équation de preuve d'ellipse" class="wp-image-2087" width="332" height="197" srcset="" sizes=""></figure> </div> <p> Par conséquent, à partir du théorème de Pythagore, il est possible de trouver <strong>la relation qui existe entre le demi-axe principal, le demi-axe secondaire et la distance semi-focale d’une ellipse :</strong>” title=”Rendered by QuickLaTeX.com” height=”195″ width=”582″ style=”vertical-align: -5px;”></p> <p> أ^2=ب^2+ج^2</p> <p class=$ $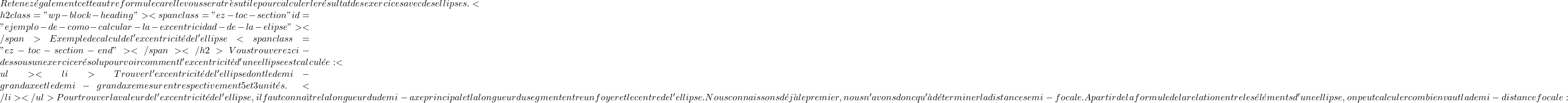Retenez également cette autre formule car elle vous sera très utile pour calculer le résultat des exercices avec des ellipses. <h2 class="wp-block-heading"><span class="ez-toc-section" id="ejemplo-de-como-calcular-la-excentricidad-de-la-elipse"></span> Exemple de calcul de l’excentricité de l’ellipse<span class="ez-toc-section-end"></span></h2> <p> Vous trouverez ci-dessous un exercice résolu pour voir comment l’excentricité d’une ellipse est calculée :</p> <ul> <li> Trouver l’excentricité de l’ellipse dont le demi-grand axe et le demi-grand axe mesurent respectivement 5 et 3 unités.</li> </ul> <p> Pour trouver la valeur de l’excentricité de l’ellipse, il faut connaître la longueur du demi-axe principal et la longueur du segment entre un foyer et le centre de l’ellipse. Nous connaissons déjà le premier, nous n’avons donc qu’à déterminer la distance semi-focale. A partir de la formule de la relation entre les éléments d’une ellipse, on peut calculer combien vaut la demi-distance focale : ” title=”Rendered by QuickLaTeX.com” height=”193″ width=”2952″ style=”vertical-align: -5px;”></p> <p> أ^2=ب^2+ج^2 ج^2=أ^2-ب^2 ج=\sqrt{a^2-b^2} = \sqrt{5^2-3^2}=\sqrt {16} = 4</p> <p class=$ $Et quand on connaît déjà la valeur des termes$