عدم التحديد اللانهائي بين اللانهاية (∞/∞)

نشرح في هذا المقال كيفية حساب ما لا نهاية من عدم التحديد بين ما لا نهاية (∞/∞). ستجد أمثلة على عدم التحديد هذا مع جميع أنواع الدوال: الدوال متعددة الحدود، والدوال الجذرية، والدوال الأسية، وما إلى ذلك. بالإضافة إلى ذلك، سوف تكون قادرًا على التدرب من خلال التمارين التي تم حلها خطوة بخطوة للحدود والتي تعطي تحديدات لا نهائية بين اللانهاية.

كيفية حل عدم التحديد اللانهائي بين اللانهائي

عندما تعطي نهاية الدالة اللانهاية مقسومة على اللانهاية، فهذا يعني أنها غير محددة (أو شكل غير محدد). لحل نهاية الدالة التي تعطي ما لا نهاية من عدم التحديد بين ما لا نهاية، يجب مقارنة درجة كثير الحدود البسط مع درجة كثير الحدود المقام.

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

تعتمد نتيجة اللانهاية مقسومة على اللانهاية على درجة البسط ودرجة مقام الكسر:

إذا كانت درجة كثير الحدود البسط أقل من درجة كثير الحدود المقام، فإن ما لا نهاية عدم التحديد مقسومًا على ما لا نهاية يساوي صفرًا.
إذا كانت درجة كثير الحدود في البسط تعادل درجة كثير الحدود المقام، فإن عدم التحديد اللانهائي على اللانهاية هو حاصل قسمة المعاملات الرئيسية لكثيرتي الحدود.
إذا كانت درجة كثير الحدود البسط أكبر من درجة كثير الحدود المقام، فإن ما لا نهاية من عدم التحديد بين ما لا نهاية يعطي ما لا نهاية أكثر أو أقل (تعتمد الإشارة على المصطلحين الرئيسيين لكثيرتي الحدود).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”></p> </p> <h2 class=$ أمثلة على اللانهاية بين اللانهاية

دعونا نرى كيف يتم حل صيغة اللانهاية غير المحددة بين اللانهاية من خلال النظر في عدة أمثلة لكل حالة:

درجة البسط أقل من درجة المقام

كما رأينا أعلاه، عندما تكون درجة كثير الحدود البسط أقل من درجة كثير الحدود المقام، فإن الحد غير المحدد بين اللانهاية يعطي دائمًا 0.

مثال 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

كثيرة حدود البسط هي من الدرجة الثانية، بينما كثيرة حدود المقام هي من الدرجة الثالثة، لذا فإن حل النهاية هو 0.

مثال 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

دالة كثيرة الحدود للبسط هي من الدرجة الأولى، لكن دالة المقام هي من الدرجة الرابعة، لذا فإن نهاية اللانهاية السالبة هي 0.

درجة البسط تساوي درجة المقام

عندما تكون درجة كثير الحدود البسط مساوية لدرجة كثير الحدود المقام، يتم حساب الحد غير المحدد اللانهاية على اللانهاية عن طريق قسمة المعاملات الرائدة (معامل حد الدرجة الأعلى) لكثيرتي الحدود.

مثال 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

في هذه الحالة، كثيرتا الحدود من الدرجة الثانية، لذلك من الضروري تقسيم معاملات حدود الدرجة الأعلى لإيجاد النهاية عند موجب اللانهاية.

مثال 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

على الرغم من أن النهاية تكون عندما تميل x إلى ناقص اللانهاية، فإن عدم التحديد اللانهائي بين اللانهاية يتم حله بنفس الطريقة.

درجة البسط أكبر من درجة المقام

عندما تكون درجة كثير الحدود البسط أكبر من درجة كثير الحدود المقام، فإن الشكل غير المحدد لللانهاية بين اللانهاية سيعطي دائمًا اللانهاية، ويتم تحديد علامة اللانهاية من خلال شروط الدرجة الأعلى لكلتي الحدود.

مثال 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

وظيفة البسط لها درجة أعلى من وظيفة المقام، وبالتالي فإن عدم التعيين اللانهائي على اللانهاية يعطي اللانهاية. وفي هذه الحالة أيضًا، يحصل كل من البسط والمقام على ما لا نهاية موجبة، لذا يجب أن تكون نتيجة النهاية موجبة أيضًا.

مثال 6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

في هذه المشكلة، يتم الحصول على ما لا نهاية موجبة من البسط لأن أي حد مربع يكون موجبًا، ومن ناحية أخرى، يتم الحصول على ما لا نهاية سالبة من المقام. ومن ثم، فإن النهاية الناتجة تكون سالبة؛ لأن موجب مقسومًا على سالب يساوي سالبًا.

اللانهائية اللانهائية بين اللانهاية مع الجذور

لقد رأينا للتو كيفية حساب عدم التحديد اللانهائي بين اللانهاية عندما يكون لدينا دوال كثيرة الحدود. لكن… ما مقدار قسمة اللانهاية على اللانهاية إذا كان لدينا جذور؟

درجة الدالة غير المنطقية (الدالة ذات الجذور) هي حاصل القسمة بين درجة الحد الرئيسي ومؤشر الجذر.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

لذلك، إذا كانت نهاية الدالة ذات الجذور تعطي عدم التعيين بين اللانهاية ، فيجب علينا تطبيق نفس القواعد الموضحة أعلاه لدرجات البسط والمقام، ولكن مع الأخذ في الاعتبار أن درجة كثيرة الحدود ذات الجذور يتم حسابها بشكل مختلف.

انظر إلى المثال التالي لنهاية ما لا نهاية لدالة ذات جذور:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

درجة البسط هي 2 ودرجة المقام هي 4 (8/2=4)، وبالتالي فإن النهاية هي 0 لأن درجة البسط أقل من درجة المقام.

من ناحية أخرى، إذا كانت درجة البسط والمقام متساوية، لحساب النهاية غير المعينة، يجب أن نأخذ المعامل الرئيسي مع الجذر:

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

عدم التحديد اللانهائي بين اللانهاية مع الدوال الأسية

أخيرًا، كل ما علينا فعله هو دراسة حالة حاصل عدم التحديد لللانهاية: ما هو مقدار عدم التحديد اللامتناهي بين اللانهاية والدوال الأسية.

نمو الدالة الأسية أكبر بكثير من نمو دالة كثيرة الحدود، لذلك يجب أن نأخذ في الاعتبار أن درجة الدالة الأسية أكبر من درجة الدالة كثيرة الحدود.

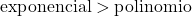$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”></p> </p> <p style=$ لذلك، إذا كانت عدم التحديد اللانهائي مقسومًا على ما لا نهاية ناتجًا عن نهاية ذات دوال أسية، فيكفي تطبيق نفس القواعد الموضحة لدرجات البسط والمقام، ولكن مع الأخذ في الاعتبار أن الدالة الأسية ذات ترتيب أعلى من كثيرة الحدود. .

بالإضافة إلى ذلك، إذا كانت لدينا دوال أسية في بسط ومقام القسمة، فإن الدالة الأسية ذات القاعدة الأكبر ستكون ذات ترتيب أعلى.

$\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

في هذه الحالة، يتكون المقام من دالة أسية، لذا فهو ذو مرتبة أعلى من البسط. ولذلك يختفي شكل اللانهاية غير المعين بين اللانهاية.

حل تمارين عدم التحديد اللانهائي بين ما لا نهاية

التمرين 1

احسب نهاية الدالة العقلانية التالية:

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

انظر الحل

عند حساب النهاية، نحصل على عدم التعيين اللانهائي بين ما لا نهاية، لكن بما أن درجة البسط أقل من درجة المقام، فإن النهاية غير المحددة تساوي صفرًا.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

تمرين 2

حل الحد غير المحدد التالي:

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

انظر الحل

عند محاولة حساب النهاية، يتم الحصول على عدم التعيين ∞/∞. في هذه الحالة، درجة كثير الحدود البسط أكبر من درجة كثير الحدود المقام، وبالتالي فإن الحد غير المحدد يساوي زائد ما لا نهاية.

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

التمرين 3

حل النهاية التالية عند اللانهاية:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

انظر الحل

النهاية تعطي عدم التعيين ناقص اللانهاية بين زائد اللانهاية. درجة البسط أكبر من درجة المقام، وبالتالي فإن النهاية غير المحددة تساوي زائد ما لا نهاية. ومع ذلك، بما أن القسمة هي سالب ما لا نهاية على موجب ما لا نهاية، فإن النتيجة هي سالب ما لا نهاية.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

التمرين 4

حل الحد غير المحدد التالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

انظر الحل

في هذه المسألة، يتم الحصول على الصورة غير المعينة اللانهائية على اللانهاية من حاصل قسمة كثيرتي حدود من نفس الدرجة، وبالتالي فإن نتيجة النهاية غير المعينة هي تقسيم معاملاتهما الرئيسية:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

التمرين 5

احسب النهاية التالية على الأقل إلى ما لا نهاية:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

انظر الحل

درجة التعبير الجبري للبسط أقل من درجة التعبير الجبري للمقام، وبالتالي فإن عدم التعيين +∞/+∞ يعطي 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

التمرين 6

حل النهاية غير المحددة التالية للدالة ذات الجذور:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

انظر الحل

تعبير البسط يقع تحت جذري، لذا فإن درجته هي 7/3. ومن ناحية أخرى، فإن كثيرة الحدود في المقام هي تربيعية. وبما أن 7/3>2، فإن النهاية تعطي زائد ما لا نهاية:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

التمرين 7

حدد نهاية ما لا نهاية للدالة التالية بالكسور:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

انظر الحل

في هذا التمرين، يتم الحصول على عدم التحديد ناقص اللانهاية مقسومًا على ناقص اللانهاية عندما تكون درجة البسط أكبر من درجة المقام، وبالتالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

التمرين 8

أوجد النهاية على الأقل إلى ما لا نهاية للدالة التالية:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

انظر الحل

كثير الحدود المقام هو تربيعي، في حين أن كثير الحدود البسط خطي. لذلك، فإن ما لا نهاية من عدم التحديد مقسومًا على ما لا نهاية يعطي 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

التمرين 9

حل الحد اللانهائي على الأقل للدالة التالية:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

انظر الحل

البسط له درجة أكبر من المقام، وبالتالي فإن نتيجة الصورة غير المحددة ∞/∞ ستكون لا نهائية. بالإضافة إلى ذلك، علامة اللانهاية ستكون سالبة لأن الموجب مقسومًا على السالب يعطي السالب:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

التمرين 10

حل النهاية التالية مع عدم التحديد اللانهائي بين ما لا نهاية:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

انظر الحل

الدالة الأسية ذات ترتيب أعلى من الدالة كثيرة الحدود، وبالتالي فإن النهاية ستعطي ما لا نهاية. لكن بقسمة الموجب على السالب تكون علامة اللانهاية سالبة:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

التمرين 11

احسب الحد التالي:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

انظر الحل

في هذه المشكلة، يتم حل عدم التعيين اللانهائي على اللانهاية عن طريق قسمة المعاملات السائدة لكثيرتي الحدود، حيث أنهما من نفس الدرجة:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

التمرين 12

حل نهاية الدالة التالية عندما تقترب x من اللانهاية:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

انظر الحل

على الرغم من أن المجهول في البسط لا يتم تربيعه بشكل مباشر، إلا أنه عند حل المتطابقة البارزة يمكننا أن نرى بوضوح أن درجة البسط أكبر من درجة المقام. حتى الآن:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

التمرين 13

احسب نهاية ما لا نهاية للدالة التالية باستخدام الجذر التكعيبي:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

انظر الحل

يتكون البسط من جذر تكعيبي، لذا فإن درجته هي 3/3=1. ومن ثم تكون درجة البسط مساوية لدرجة المقام، وبالتالي يتم حل اللانهائية بين اللانهاية على النحو التالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

التمرين 14

حل النهاية إلى ما لا نهاية للدالة التالية مع جذرين:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

انظر الحل

درجة البسط هي 7/3 = 2.33 ودرجة المقام هي 5/2 = 2.5. ولذلك، بما أن درجة البسط أقل من درجة المقام، فإن الحد اللانهائي غير المحدد بين ما لا نهاية هو 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

التمرين 15

احسب الحد التالي:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

انظر الحل

بغض النظر عن درجة البسط، بما أن لدينا دالة أسية في المقام، فإن نتيجة الصيغة غير المحددة اللانهاية على اللانهاية هي 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

كيفية حل عدم التحديد اللانهائي بين اللانهائي

درجة البسط أقل من درجة المقام

مثال 1:

مثال 2:

درجة البسط تساوي درجة المقام

مثال 3:

مثال 4:

درجة البسط أكبر من درجة المقام

مثال 5:

مثال 6:

اللانهائية اللانهائية بين اللانهاية مع الجذور

عدم التحديد اللانهائي بين اللانهاية مع الدوال الأسية

حل تمارين عدم التحديد اللانهائي بين ما لا نهاية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

التمرين 7

التمرين 8

التمرين 9

التمرين 10

التمرين 11

التمرين 12

التمرين 13

التمرين 14

التمرين 15

اترك تعليقاً إلغاء الرد