ضرب عدد في مصفوفة

في هذه الصفحة سنرى كيفية ضرب رقم في مصفوفة. لديك أيضًا أمثلة ستساعدك على فهم الأمر بشكل مثالي وحل التمارين حتى تتمكن من التدرب عليها. سوف تجد أيضًا جميع خصائص منتج العددية والمصفوفة.

كيفية ضرب رقم في مصفوفة؟

لضرب رقم في مصفوفة ، قم بضرب كل عنصر من عناصر المصفوفة في الرقم.

مثال:

حل مسائل ضرب رقم في مصفوفة

التمرين 1:

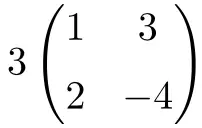
حل تمرين ضرب عدد بمصفوفة 2x2، العمليات على المصفوفات

انظر الحل

إنه ضرب عددي في مصفوفة مربعة من الرتبة 2:

$\displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}$

تمرين 2:

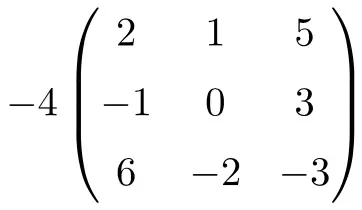
تمرين تم حله خطوة بخطوة لضرب عدد في مصفوفة 3x3، العمليات على المصفوفات

انظر الحل

هو حاصل ضرب عدد في مصفوفة مربعة من الرتبة 3:

$\displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}$

التمرين 3:

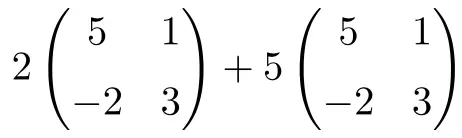
حل تمرين ضرب عدد في مصفوفة 2x2، العمليات المدمجة مع المصفوفات

انظر الحل

هي عملية تجمع بين منتجات الأعداد بالمصفوفات ومجموع المصفوفات ذات البعد 2×2:

$\displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}$

لذلك، علينا أولاً إيجاد المنتجات:

$\displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}$

وأخيرًا نضيف المصفوفات الناتجة:

$\displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}$

التمرين 4:

النظر في المصفوفات التالية:

$\displaystyle A=\begin{pmatrix} 2 & -3 & 5 \\ 1 & 4 & 0 \\ -3 & 2 & -5 \end{pmatrix} \qquad B=\begin{pmatrix} 6 & 0 & 2 \\ -3 & 4 & 1 \\ 3 & 2 & 7 \end{pmatrix}$

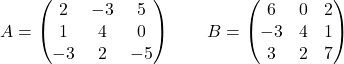
احسب:

$\displaystyle -2A+5I-3B$

انظر الحل

هي عملية تجمع بين الضرب العددي والجمع والطرح للمصفوفات ذات البعد 3×3. علاوة على ذلك، المصفوفة

$I$

هي مصفوفة الهوية، والتي تتكون من 1 على القطر الرئيسي و0 على بقية العناصر:

$\displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}$

لذلك، نقوم أولاً بإجراء الضرب:

$\displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

نضيف المصفوفتين الأوليين:

$\displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

وأخيرًا، نقوم بطرح المصفوفات:

$\displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}$

إذا كانت هذه التمارين على نواتج المصفوفات العددية مفيدة لك، فلا تتردد في التدرب على حل التمارين خطوة بخطوة حول جمع المصفوفات وحاصل ضرب المصفوفات ، نوعي عمليات المصفوفات التي تتكرر أكثر.

خواص حاصل ضرب عدد في مصفوفة

كما تعلمون، هناك أنواع عديدة من المصفوفات : المصفوفات المربعة، والمصفوفات المثلثية، ومصفوفة الوحدة، وما إلى ذلك. لكن، لحسن الحظ، جميع خصائص حاصل ضرب الأعداد في المصفوفات صالحة لجميع فئات المصفوفات.

فيما يلي خصائص الضرب بين الكميات القياسية والمصفوفات:

ملكية مشتركة:

$a \cdot (b \cdot A) = (a \cdot b) \cdot A$

انظر إلى العمليتين التاليتين لأنهما تعطيان نفس النتيجة مهما ضربنا 2 و 3:

$\displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

$\displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

خاصية التوزيع فيما يتعلق بإضافة الكميات:

$(a+b) \cdot A = a \cdot A+ b \cdot A$

كما ترون في المثال أدناه، الأمر نفسه إذا أضفنا أولاً 1+2 ثم ضربناه في مصفوفة، أو إذا ضربنا المصفوفة بشكل منفصل في 1 وفي 2 ثم أضفنا النتائج:

$\displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

$\displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

خاصية التوزيع فيما يتعلق بإضافة المصفوفة:

$a \cdot \left(A + B \right) = a \cdot A + a \cdot B$

بمعنى آخر، فإن إضافة مصفوفتين رياضيتين ثم ضربهما في رقم يعادل ضرب المصفوفتين بشكل منفصل في نفس الرقم ثم جمع النتائج. في المثال أدناه يمكنك التحقق من:

$\displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

$\displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

خاصية العنصر المحايد:

$1 \cdot A = A$

لذلك، عند ضرب مصفوفة في 1، لا نقوم بتعديل المصفوفة:

$\displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}$

هذه كلها خصائص حاصل ضرب العدد القياسي والمصفوفة، وهذه نهاية هذه المقالة. نأمل أن تكون قد نالت إعجابك، وقبل كل شيء، أن تكون قد تعلمت كيفية حل ضرب الأعداد باستخدام المصفوفات.

ومن ناحية أخرى، هناك عمليات مصفوفية أخرى مرتبطة بالضرب، وهي مفيدة جدًا، وهي القوى. هنا نترك لك الصفحة التي ستتعرف فيها على ماهيتها وكيفية حل قوة المصفوفة ، في حال كنت مهتمًا بالفضول.

كيفية ضرب رقم في مصفوفة؟

مثال:

حل مسائل ضرب رقم في مصفوفة

التمرين 1:

تمرين 2:

التمرين 3:

التمرين 4:

خواص حاصل ضرب عدد في مصفوفة

اترك تعليقاً إلغاء الرد