▷ كيفية حساب نقطة المنتصف للمقطع؟ (معادلة)

تشرح هذه الصفحة معنى نقطة المنتصف للقطعة. بالإضافة إلى ذلك، سوف تكتشف كيفية العثور على منتصف القطعة باستخدام صيغتها. سترى أيضًا أمثلة وتمارين ومسائل تم حلها لنقاط منتصف القطعة.

ما هي نقطة المنتصف للقطعة؟

في الرياضيات، نقطة المنتصف للقطعة هي النقطة التي تقع على نفس المسافة من طرفي القطعة. وبالتالي فإن الوسط يقسم القطعة إلى جزأين متساويين.

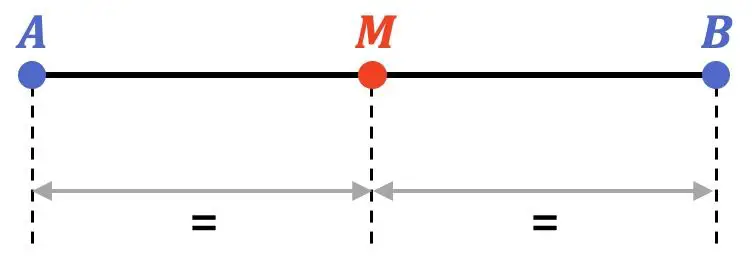
بالإضافة إلى ذلك، فإن نقطة المنتصف تقع مباشرة في وسط القطعة، لذا فهي تنتمي إلى منصف القطعة.

ومن ناحية أخرى، فإن نقطة المنتصف للقطعة هي أيضًا نقطة متساوية البعد عن عنصرين هندسيين: طرفي القطعة.

كيفية حساب نقطة المنتصف للقطعة؟

بالنظر إلى الإحداثيات الديكارتية للنقاط القصوى للقطعة:

$A(x_1,y_1) \qquad B(x_2,y_2)$

تتوافق إحداثيات منتصف القطعة المذكورة مع نصف مجموع إحداثيات النقاط القصوى:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

هذه هي صيغة منتصف القطعة في المستوى الديكارتي (في R2). لكن من الواضح أن الصيغة تنطبق أيضًا على الفضاء الديكارتي (في R3)، فأنت تحتاج فقط إلى إضافة نصف مجموع الإحداثي Z:

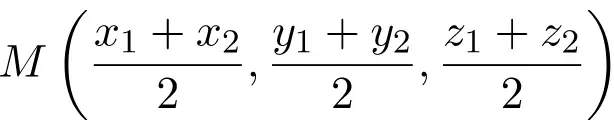
دعونا نلقي نظرة على مثال لكيفية حساب إحداثيات نقطة منتصف القطعة:

حدد نقطة منتصف القطعة المكونة من النقاط التالية:

$A(2,5) \qquad B(4,-1)$

للعثور على منتصف القطعة، ما عليك سوى تطبيق الصيغة الخاصة بها:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

تمارين محلولة في وسط القطعة

التمرين 1

ما نقطة منتصف القطعة التي طرفاها هي النقطتان التاليتان؟

$A(3,-2) \qquad B(5,8)$

انظر الحل

للعثور على منتصف القطعة يجب عليك تطبيق الصيغة مباشرة:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

تمرين 2

أوجد إحداثيات نقطة نهاية القطعة المستقيمة التي تبدأ من النقطة A ونقطة منتصفها M.

$A(4,-1) \qquad M(-2,1)$

انظر الحل

في هذه الحالة، نعرف إحداثيات نقطة البداية ووسط القطعة. لذلك، نعوض بالإحداثيات التي نعرفها في صيغة نقطة منتصف القطعة:

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

والآن نوجد إحداثيات نقطة نهاية القطعة من المعادلة السابقة:

إحداثيات X

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

إحداثيات ص

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

وبالتالي فإن إحداثيات النهاية النهائية للقطعة هي:

$\bm{B(-8,3)}$

التمرين 3

بالنظر إلى متوازي الأضلاع التالي:

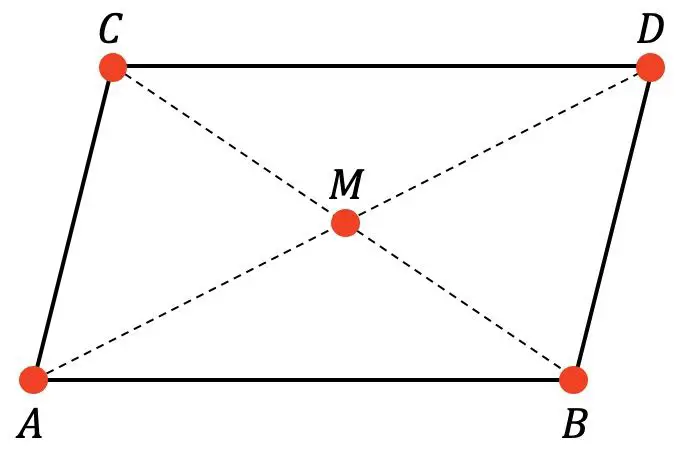
نحن نعلم أن M هو مركز متوازي الأضلاع وأن إحداثيات النقاط A وB وC هي:

$A(1,1) \quad B(5,1) \quad C(7,3)$

من هذه المعلومات وباستخدام صيغة نقطة المنتصف، احسب إحداثيات النقطة D.

انظر الحل

للعثور على إحداثيات النقطة D باستخدام صيغة منتصف القطعة، يجب عليك أولاً حساب إحداثيات النقطة M ثم إحداثيات النقطة D.

النقطة M هي نقطة منتصف القطعة BC، وبالتالي فإن إحداثياتها هي:

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

وبمجرد أن نعرف النقطة M، يمكننا إيجاد النقطة D. النقطة M هي أيضًا منتصف القطعة AD، لذا:

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

الإحداثي X للنقطة D

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

إحداثي Y للنقطة D

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

وبالتالي فإن إحداثيات النقطة D هي:

$\bm{D(11,3}$

التمرين 4

احسب المعادلة المستمرة للخط المستقيم المتعامد مع القطعة PQ عند منتصفها. كن النقاط

$P(1,4)$

$Q(5,-2).$

انظر الحل

لتحديد معادلة الخط، نحتاج إلى متجه اتجاهه ونقطة تشكل جزءًا من الخط.

في هذه الحالة، سيكون متجه الاتجاه للخط عموديًا على المتجه

$\vv{PQ}.$

ولذلك فإننا نحسب المتجه

$\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

ويمكننا إيجاد متجه عمودي على آخر بتغيير مركبات المتجه بينهما ثم تغيير إشارة المركبة، وبالتالي:

$\vv{PQ}_\perp =(6,4)$

لدينا الآن متجه اتجاه الخط، لذا نحتاج فقط إلى نقطة واحدة تنتمي إلى الخط. في هذه الحالة، تخبرنا التعليمات أن الخط يمر بنقطة منتصف القطعة، لذا نحسب نقطة المنتصف باستخدام الصيغة:

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

وأخيرًا، نقوم ببناء المعادلة المستمرة للخط من النقطة والمتجه المحسوبين:

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

ما هي نقطة المنتصف للقطعة؟

كيفية حساب نقطة المنتصف للقطعة؟

تمارين محلولة في وسط القطعة

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد