▷ ذات الحدين لنيوتن (أو نظرية ذات الحدين)

ستجد في هذه الصفحة شرحا لماهية ذات الحدين (أو نظرية ذات الحدين) لنيوتن وما هي صيغتها. يمكنك أيضًا أن ترى كيف يمكن تبسيط ذلك باستخدام مثلث تارتاليا (أو باسكال). بالإضافة إلى ذلك، ستجد تمارين محلولة خطوة بخطوة بشأن ذات الحدين لنيوتن وجميع خصائصها. وأخيرًا، سنشرح الفضول وراء أصل هذه النظرية الخاصة جدًا.

ما هي ذات الحدين لنيوتن؟

في الرياضيات، ذات الحدين لنيوتن ، والمعروفة أيضًا باسم نظرية ذات الحدين ، هي صيغة تسمح لك بحساب قوة ذات الحدين بسهولة. بمعنى آخر، تتكون ذات الحدين لنيوتن من صيغة يمكن من خلالها ^حل التعابير الجبرية على الصورة (أ+ب).

ومن الواضح أن هذه النظرية سميت على اسم الفيزيائي والرياضي والفيلسوف السير إسحاق نيوتن. ومع ذلك، هناك بعض الجدل في هذا الصدد حيث تم العثور على نصوص شرق أوسطية حيث كانت هذه النظرية قيد الاستخدام بالفعل. أدناه سنناقش بعمق أصل هذه الصيغة الرياضية.

صيغة نيوتن ذات الحدين

وكما رأينا في تعريف ذات الحدين لنيوتن، فإن هذه النظرية تستخدم لحل قوى ذات الحدين. لكن… كيف يتم تطبيق ذات الحدين لنيوتن؟ أو بمعنى آخر ما هي صيغة نيوتن ذات الحدين؟

الصيغة الرياضية ذات الحدين لنيوتن هي كما يلي:

$\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k$

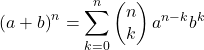
أو ما يعادلها:

$\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}$

الصيغة معقدة بعض الشيء لفهم مفهوم ذات الحدين لنيوتن، لذلك قمنا بعرض قوى ذات الحدين من أدنى درجة أدناه حتى تتمكن من فهمها بشكل أفضل:

كما ترون، عند توسيع ذات الحدين ، تنخفض أسس الحد الأول (أ) بينما تزداد أسس الحد الثاني (ب) ، تمامًا كما يزيد العنصر الأدنى في الأعداد التوافقية.

لذلك، لاستخدام نظرية ذات الحدين، تحتاج إلى معرفة كيفية حل رقم اندماجي، أي التعبير الجبري من النوع

$\begin{pmatrix} 4 \\ 2 \end{pmatrix}$

. لذلك، قبل أن ننظر إلى أمثلة حول كيفية حساب ذات الحدين لنيوتن، دعونا نراجع بإيجاز الأعداد التوافقية.

رقم اندماجي

لتحديد رقم اندماجي (أو معامل ذو الحدين) يجب عليك تطبيق الصيغة التالية:

$\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}$

ذهب

$n!$

$k!$

هذه أرقام عاملية . دعونا نتذكر أيضًا أنه يتم حساب الرقم الضربي عن طريق ضرب جميع الأعداد الصحيحة الموجبة للـ 1 في الرقم المذكور:

$n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n$

على سبيل المثال، سنجد رقمًا اندماجيًا حتى تتمكن من رؤية كيفية القيام بذلك:

$\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4$

يمكن أيضًا تحديد الأرقام التوافقية عبر الآلة الحاسبة باستخدام المفتاح

$\boxed{nCr}.$

نيوتن أمثلة ذات الحدين

الآن بعد أن عرفنا ما هي نظرية ذات الحدين، دعونا نرى كيفية تطبيق صيغة نيوتن ذات الحدين باستخدام مثالين عدديين.

مثال 1

طبّق ذات الحدين لنيوتن لحساب قوة الحدين التاليين:

$(x+3)^2$

من الواضح أنه بما أن هذه ذات الحدين مربعة، فيمكن حلها أيضًا باستخدام صيغ المتطابقات البارزة ( كيفية حل المتطابقات البارزة )، لكننا سنحسبها باستخدام نظرية ذات الحدين كمثال.

أولا، يجب علينا تطبيق صيغة نيوتن ذات الحدين:

في هذه الحالة ن = 2، وبالتالي:

$\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}$

أنظر جيداً، في البداية نرفع الحد الأول (x) إلى الحد الأقصى الممكن، وهو في هذه الحالة هو 2. ومن ناحية أخرى، نرفع الحد الثاني (3) إلى الحد الأدنى الممكن، وهو دائماً 0. لكن عندما نتجه إلى اليمين، نحتاج إلى رفع الحد الأول إلى رقم أقل من السابق والحد الثاني إلى رقم أعلى من السابق.

الآن دعونا نحسب الأرقام التوافقية:

$\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}$

نحن نحل للقوى:

$\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9$

وأخيرًا، نحسب الضرب:

$\left( x+3\right)^2 =x^2 + 6x + 9$

مثال 2

الآن سنقوم بحل مشكلة أكثر صعوبة قليلاً.

قم بتطبيق صيغة نيوتن ذات الحدين لإيجاد قوة ذات الحدين التالية:

$(2x+1)^3$

صيغة نظرية ذات الحدين هي:

في هذه الحالة ن = 3، وبالتالي:

$\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}$

نحسب الأعداد التوافقية:

$\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}$

الآن نحل القوى، لذلك من المهم أن تتذكر الخاصيتين التاليتين:

• عندما يتم رفع وحيدة الحد إلى الأس، يتم رفع المعامل والمتغير إلى نفس الأس →

$(2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3$

• أي حد يصل إلى 0 يعطي 1 →

$(2x)^0=1$

لذلك نجد القوى من خلال هاتين الخاصيتين:

$\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1$

$\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1$

وأخيرًا، نضرب المصطلحات:

$\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1$

ذات الحدين لنيوتن ومثلث تارتاليا (أو باسكال).

كما رأيت في الأمثلة أعلاه، فإن حساب الأرقام التوافقية أمر ممل بعض الشيء. لهذا السبب، سنعلمك خدعة حتى لا تضطر إلى حل الأعداد التوافقية، حيث يمكنك معرفة قيمتها مباشرة باستخدام مثلث تارتاليا، المعروف أيضًا باسم مثلث باسكال.

في حال كنت لا تعرف ما هو، مثلث تارتاغليا ، ويسمى أيضًا مثلث باسكال ، هو تمثيل رياضي للأرقام مرتبة في شكل مثلث.

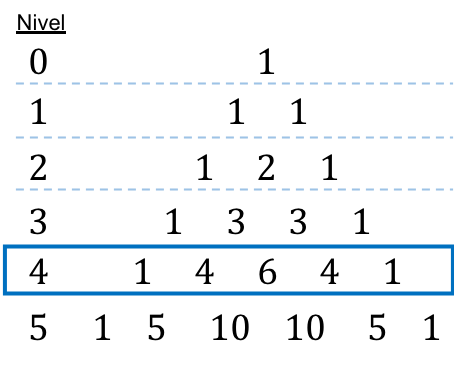
لبناء مثلث تارتاليا أو باسكال يجب أن نبدأ من قمة المثلث والتي تكون دائما 1، ومن ثم يتم تحديد أرقام الخطوط الموجودة أدناه. كل رقم في السطور التالية يساوي مجموع الرقمين اللذين فوقه مباشرة، ما عدا نهايتي السطور التي تكون دائمًا 1.

نيوتن زوج 1 المدرسة الثانوية على الانترنت

إذن، كل رقم من هذه الأرقام في مثلث تارتاليا يتوافق مع نتيجة رقم اندماجي، انظر إلى الشكل التالي:

على سبيل المثال، معامل ذات الحدين

$\begin{pmatrix} 3 \\ 1 \end{pmatrix}$

يعادل 3، لأنه في مثلث تارتاليا يوجد 3 في موضعه.

لذلك يمكننا استخدام مثلث تارتاغليا (أو مثلث باسكال) لحل ذات الحدين لنيوتن بسرعة أكبر بكثير، لأنه يوفر علينا حسابات الأعداد التوافقية.

على سبيل المثال، إذا أردنا إجراء التعزيز التالي لقيمة ذات الحدين:

$(x+5)^3$

وبتطبيق قاعدة نيوتن ذات الحدين نحصل على التعبير الجبري التالي:

$\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}$

حسنًا، بدلًا من حساب الأعداد الاندماجية واحدًا تلو الآخر، يمكننا ببساطة استبدال كل رقم اندماجي بمعامله المقابل في مثلث تارتاليا. في هذه الحالة يتم رفع ذات الحدين إلى المستوى الثالث، وبالتالي فهي تتوافق مع المستوى الثالث للمثلث:

مثلث تارتاجليا أو مثلث باسكال وذو الحدين لنيوتن

$\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}$

والآن كل ما علينا فعله هو القيام بالعمليات المتبقية:

$\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125$

$\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125$

كما ترون، يتم استخدام مثلث تارتاليا (أو باسكال) لحساب ذات الحدين لنيوتن بطريقة أبسط وأسرع، كما أظهرنا. ولهذا السبب نوصي باستخدامه.

لتلخيص كل ما رأيناه حتى الآن، نترككم مع صورة توضح كيف تبدو تعبيرات ذات الحدين لنيوتن مع أرقام مثلث تارتاليا (أو باسكال):

ذات الحدين لنيوتن ومثلث باسكال أو تارتاليا

ذات الحدين السالبة لنيوتن: قوة الطرح

حتى الآن، جميع أمثلة ذات الحدين لنيوتن التي قمنا بحلها كانت مجرد إضافات. من ناحية أخرى، عندما يكون لأحد حدي ذات الحدين علامة سلبية، يظل الإجراء مشابهًا ولكنه يتغير قليلاً.

عندما يكون أحد حدود ذات الحدين سالبًا، أي أنه طرح من النوع (ab) ⁿ ، فإن علامات مفكوك ذات الحدين لنيوتن يجب أن تتناوب على الصورة + – + – + – + – …

قمنا أدناه بتطوير قوى ذات الحدين السالبة للدرجات الخمس الأولى باستخدام نظرية ذات الحدين ومع معاملات مثلث تارتاليا الموجودة بالفعل، بحيث يمكنك العثور مباشرة على التعبير ذي الحدين الذي تحتاجه:

خصائص ذات الحدين لنيوتن

تتميز تعبيرات نيوتن ذات الحدين بالخصائص التالية:

يؤدي تحليل ذات الحدين لنيوتن دائمًا إلى الحصول على حد واحد أكبر من درجة ذات الحدين. أو بمعنى آخر للزوج
$(a+b)^n$

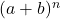
لقد تأثروا

$n+1$

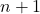
شروط.
صلاحيات العنصر
$a$

أبدا ب

$n$

وتنخفض حتى تصل إلى 0 في الربع الأخير.
صلاحيات العنصر
$b$

يذهبون في الاتجاه الآخر: يبدأون من 0 ويزدادون حتى يصلوا

$n$

في الفصل الأخير.
لكل عنصر من عناصر ذات الحدين لنيوتن، مجموع الأسس
$a$

و

$b$

مساوي ل

$n.$
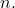
معامل الحد الأول من تعبير نيوتن ذو الحدين هو دائمًا 1 (موجب) والمعامل الثاني يعادل أس ذات الحدين (موجب أو سالب).

احسب الحد k من ذات الحدين لنيوتن

على الرغم من أن هذا أمر غير معتاد، إلا أننا قد نواجه في بعض الأحيان مشكلات، حيث يُطلب منا، بدلاً من القيام بتوسيع ذات الحدين لنيوتن، تحديد الحد k من ذات الحدين لنيوتن، أي الحد الذي يحتل الموضع k.

وبالتالي، لحساب الحد الذي يشغل المكان k في ذات الحدين لنيوتن، يجب علينا استخدام صيغة تعتمد على ما إذا كانت ذات الحدين عبارة عن إضافة أو طرح:

إذا كانت ذات الحدين لنيوتن موجبة، يتم حساب قيمة الحد k بالصيغة التالية:

$(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}$

إذا كانت ذات الحدين لنيوتن سالبة، يتم تحديد قيمة الحد k بالصيغة التالية:

$(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}$

على سبيل المثال، سنجد الحد الرابع من ذات الحدين من الدرجة 5 التالية:

$(x+3)^5$

وبما أنها ذات حدين مكونة من مجموع، فإننا نطبق الصيغة الأولى:

$T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}$

نستبدل المتغيرات في الصيغة بالقيم المقابلة لها:

$T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}$

ونقوم بالعمليات:

$T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}$

$T_4 = 10 \cdot x^{2}\cdot 27$

$T_4 = 270 x^{2}$

وبهذه الطريقة نكون قد حسبنا الحد الرابع من مفكوك نيوتن ذي الحدين دون الحاجة إلى حساب جميع الحدود الأخرى.

تمارين محلولة على ذات الحدين لنيوتن

الآن بعد أن شرحنا ما هي نظرية ذات الحدين، نتركك مع العديد من التمارين التي تم حلها خطوة بخطوة حول نظرية ذات الحدين لنيوتن حتى تتمكن من التدرب عليها. تذكر أيضًا أنه يمكنك ترك أي أسئلة أو اقتراحات لنا في التعليقات.

التمرين 1

قم بتوسيع القوة ذات الحدين التالية باستخدام نظرية ذات الحدين:

$(x+4)^3$

انظر الحل

نستخدم أولاً صيغة نيوتن ذات الحدين:

$\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}$

بما أن ذات الحدين مرفوعة للقوة 3، فإننا ننظر إلى المستوى الثالث لمثلث تارتاليا للعثور مباشرة على الأعداد التوافقية:

تمارين على نظرية ذات الحدين لنيوتن تم حلها خطوة بخطوة 1 ثانوية عامة

$(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3$

نقوم بتنفيذ الصلاحيات:

$1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64$

وأخيرا نضرب:

$x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64$

$\bm{x^3 + 12x^2 + 48 x + 64}$

تمرين 2

احسب القوة التالية باستخدام صيغة نيوتن ذات الحدين:

$(3x+2)^3$

انظر الحل

أولا، نطبق صيغة نيوتن ذات الحدين:

$\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}$

وبما أن ذات الحدين مكعبة، فإننا ننظر إلى المستوى الثالث لمثلث باسكال لمعرفة قيم الأعداد التوافقية بشكل مباشر:

$\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3$

نحسب قوى أحاديات الحد:

$1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8$

وأخيرًا نقوم بعملية الضرب:

$27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8$

$\bm{27x^3 + 54x^2 +36x+8}$

التمرين 3

قم بتوسيع التعبير متعدد الحدود التالي باستخدام صيغة نيوتن ذات الحدين:

$(2x-2)^3$

انظر الحل

أولا، نستخدم صيغة نيوتن ذات الحدين. لكن بما أن لدينا عملية طرح داخل القوسين، فيجب علينا تبديل علامات معاملات كل حد:

$(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3$

بما أن ذات الحدين مرفوعة للقوة ثلاثة، فإننا ننظر إلى المستوى الثالث لمثلث تارتاليا لحساب الأعداد التوافقية مباشرة:

$(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3$

نقوم بتنفيذ الصلاحيات:

$1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8$

ونحل الضرب:

$8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8$

$\bm{8x^3 -24 x^2 +24x -8}$

التمرين 4

أوجد التعبير الموسع لمعادلة نيوتن التالية باستخدام الصيغة:

$(4x-3y)^4$

انظر الحل

يجب علينا تطبيق الصيغة العامة ذات الحدين لنيوتن، ولكن كما في هذه الحالة لدينا عملية طرح بين قوسين، يجب علينا تبديل علامات كل حد:

$\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}$

بما أن ذات الحدين مرفوعة إلى المستوى الرابع، فإننا ننظر إلى المستوى 4 من مثلث تارتاليا للعثور مباشرة على الأعداد التوافقية:

$\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}$

ندرك جميع الصلاحيات:

$1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4$

وأخيرًا، نحل الضرب:

$256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4$

$\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}$

التمرين 5

حدد الحد السابع في مفكوك التعبير ذي الحدين التالي:

$(2x-5y)^{10}$

انظر الحل

وبما أنها ذات حدين سالبة، يجب علينا استخدام الصيغة التالية:

$T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}$

نريد تحديد الحد 7 ويتم رفع ذات الحدين إلى القوة 10، لذلك باستبدال القيم في الصيغة يصبح:

$T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}$

ولذلك يكفي للعمل أن نعرف مصطلح:

$\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}$

تاريخ ذات الحدين لنيوتن

على الرغم من أن أصل نظرية ذات الحدين ينسب إلى العالم الإنجليزي الشهير إسحاق نيوتن (1642-1727)، إلا أنه في الواقع تم اكتشاف الصيغة الأولى للنظرية لأول مرة على يد المهندس الفارسي الكاريجي حوالي عام 1000، بل وقد تم اكتشاف ذلك في القرن الثالث عشر، كان علماء الرياضيات الصينيون يانغ هوي وتشوه شيه تشيه يعرفون بالفعل التوسعات ذات الحدين للدرجات الصغيرة.

لاحقًا، في القرن السابع عشر، بنى نيوتن على الأسس التي وضعها علماء الرياضيات السابقون لتوسيع نظرية ذات الحدين. باستخدام أساليب عالم الرياضيات جون وولز في الاستيفاء والاستقراء ومفاهيم الأسس المعممة، كان قادرًا على تحويل تعبير متعدد الحدود إلى سلسلة لا نهائية.

حوالي عام 1665، نجح نيوتن في إثبات أن الأس n لنظرية ذات الحدين يمكن أيضًا أن يكون أسًا عقلانيًا، وهذا يعني أنه يمكن أيضًا حل قوة ذات الحدين إذا كان الأس كسرًا. ومن ناحية أخرى، فقد ثبت ذلك أيضًا في حالة الأس السالب. والمفاجأة أنه اكتشف أن تطورات التعبيرين هي سلسلة لا نهائية من المصطلحات.

مع هذا الاكتشاف، بدأ نيوتن في التشكيك في العلاقة بين المتسلسلة اللانهائية وتعبيرات متعددة الحدود المحدودة، واستنتج أنه يمكن إجراء العمليات الرياضية مع سلسلة لا نهائية بنفس طريقة تعبيرات متعددة الحدود المحدودة. على الرغم من أن نيوتن لم ينشر هذه النظرية مطلقًا، إلا أن جون وولز فعل ذلك في النهاية في عام 1685، ونسب الفضل إلى نيوتن في هذا الاكتشاف.

نيوتن ذات الحدين (نظرية ذات الحدين)

ما هي ذات الحدين لنيوتن؟

صيغة نيوتن ذات الحدين

رقم اندماجي

نيوتن أمثلة ذات الحدين

مثال 1

مثال 2

ذات الحدين لنيوتن ومثلث تارتاليا (أو باسكال).

ذات الحدين السالبة لنيوتن: قوة الطرح

خصائص ذات الحدين لنيوتن

احسب الحد k من ذات الحدين لنيوتن

تمارين محلولة على ذات الحدين لنيوتن

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

تاريخ ذات الحدين لنيوتن

اترك تعليقاً إلغاء الرد