دالة الظل الزائدية

ستجد في هذه الصفحة كل شيء عن المماس الزائدي: ما هي صيغته، تمثيله البياني، جميع خصائصه،…

صيغة الظل الزائدي

دالة الظل الزائدية هي إحدى الدوال القطعية الرئيسية ويتم تمثيلها بالرمز tanh(x) . رياضياً، المماس الزائدي يساوي جيب التمام الزائدي مقسوماً على جيب التمام الزائدي.

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

من صيغة جيب التمام الزائدية وصيغة جيب التمام الزائدية، يمكننا الوصول إلى التعبير التالي:

$\text{tanh}(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}$

لذلك، ترتبط دالة الظل الزائدية بالدالة الأسية. وفي الرابط التالي يمكنك رؤية كافة خصائص هذه الأنواع من الوظائف:

➤ انظر: خصائص الدوال الأسية

التمثيل الرسومي للظل الزائدي

من صيغتها، يمكننا تمثيل دالة الظل الزائدية بيانياً:

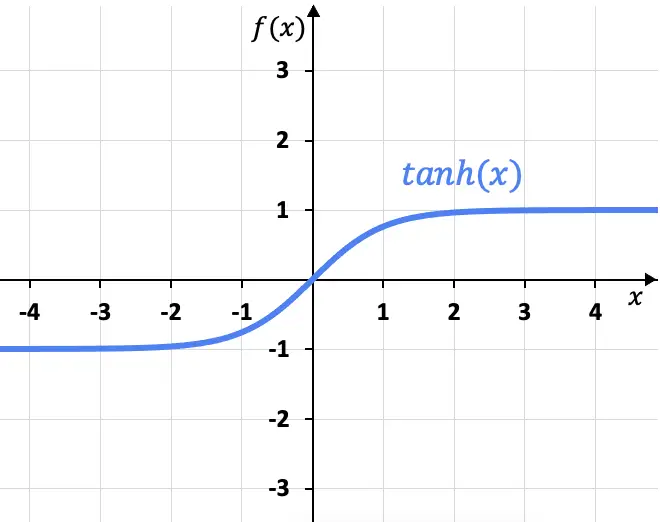
كما ترون من الرسم البياني، فإن دالة الظل الزائدية لها خطان مقاربان أفقيان عند x=+1 وx=-1، نظرًا لأن نهاية الدالة عندما تقترب x من زائد ما لا نهاية تعطي x=+1، والحد من سالب ما لا نهاية يعطي س=-1.

من ناحية أخرى، فإن الرسم البياني للظل الزائدي لا علاقة له بالرسم البياني للظل (الدالة المثلثية)، وهي دالة دورية. يمكنك مشاهدة التمثيل البياني للظل ومدى اختلافه عن الظل الزائدي في الرابط التالي:

➤ انظر: التمثيل البياني لدالة الظل

خصائص الظل الزائدي

تتميز دالة الظل الزائدية بالخصائص التالية:

مجال دالة الظل الزائدي هو كل الأعداد الحقيقية.

$\text{Dom } f = \mathbb{R}$

في المقابل، يقتصر مسار أو نطاق دالة الظل الزائدية على القيم الواقعة بين -1 و+1 (غير شاملة).

$\text{Im } f= (-1,1)$

الظل الزائدي هو دالة مستمرة وثنائية وغريبة (متماثلة بالنسبة لأصل الإحداثيات).

$\displaystyle \text{tanh}(-x) =- \text{tanh}(x)$

تتقاطع الدالة مع المحور X والمحور Y عند نقطة الأصل الإحداثية.

$(0,0)$

حدود زائد/ناقص اللانهاية لدالة الظل الزائدية تعطي +1/-1. ولذلك، فإن الدالة لها خط تقارب أفقي عند x=+1 وخط تقارب أفقي آخر عند x=-1.

$\displaystyle\lim_{x\to+\infty}\text{tanh}(x)=+1$

$\displaystyle\lim_{x\to-\infty}\text{tanh}(x)=-1$

يتزايد المماس الزائدي بشكل صارم على مجاله بأكمله، وبالتالي ليس له نقاط قصوى نسبية (لا الحد الأقصى ولا الحد الأدنى).

ومع ذلك، تتغير الدالة من محدبة إلى مقعرة عند النقطة x = 0، لذا فإن x = 0 هي نقطة انقلاب للدالة.

يُطلق على معكوس دالة الظل الزائدي اسم وسيطة الظل الزائدي (أو ظل الزاوية القطعي) وتكون صيغتها كما يلي:

$\displaystyle\text{tanh}^{-1}(x)=\text{arg tanh}(x)=\cfrac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$

مشتق دالة الظل الزائدي هو 1 مقسومًا على مربع جيب التمام الزائدي:

$f(x)=\text{tanh}(x) \ \longrightarrow \ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=1-\text{tanh}^2(x)$

تكامل دالة الظل الزائدي هو اللوغاريتم الطبيعي لجيب التمام الزائدي:

$\displaystyle\int\text{tanh}(x) \ dx= \ln\Bigl(\text{cosh}(x)\Bigr)+C$

يمكن حساب المماس الزائدي لمجموع رقمين مختلفين من خلال تطبيق المعادلة التالية:

$\text{tanh}(x+y)=\cfrac{\text{tanh}(x)+\text{tanh}(y)}{1+\text{tanh}(x)\cdot \text{tanh}(y)}$

متعددة حدود تايلور أو سلسلة الظل الزائدية لها نصف قطر التقارب
$\left|x\right|<\cfrac{\pi}{2}$

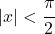
ويتوافق مع التعبير التالي:

$\displaystyle\text{tanh}(x)=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}$

ذهب

$B_n$

هو عدد برنولي .

صيغة الظل الزائدي

التمثيل الرسومي للظل الزائدي

خصائص الظل الزائدي

اترك تعليقاً إلغاء الرد