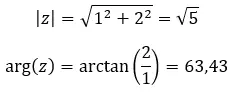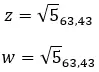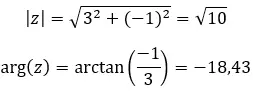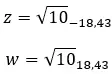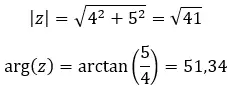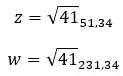في هذه المقالة، سنناقش خصائص الأعداد المركبة ، والتي يمكن أن تكون مفيدة عند حل العمليات الحسابية وتبسيط التعبيرات. دعنا ننتقل مباشرة إلى هذه الخصائص.
معامل ووسيطة عدد مركب
الخاصية الأولى للعدد المركب هي معامل ووسيطة العدد المركب. من السهل جدًا إجراء الحساب، لأنك تحتاج فقط إلى تطبيق بعض الصيغ.
صيغة حساب الوحدة:

صيغة حساب الوسيطة:

الآن، إذا تم التعبير عن العدد بالشكل القطبي أو المثلثي، فليست هناك حاجة لإجراء أي حسابات. لأنه، في نفس التعبير، يتم سرد الوحدة النمطية والوسيطة.
في الصورة أدناه يمكنك رؤية صيغة الرقم في الصورة القطبية، حيث |z| هو المعامل و α هي الوسيطة.

وفي هذه الصورة الأخرى يمكنك رؤية بنية العدد معبرًا عنها بالشكل المثلثي، حيث |z| هو المعامل و α هي الوسيطة.

أعداد معقدة متساوية
الأعداد المركبة المتساوية هي تلك التي تشترك في المعامل والوسيطة. إذن من هاتين القيمتين:

هذه هي نفسها إذا تم استيفاء الخاصية التالية.
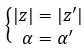
من ناحية أخرى، إذا كان لدينا كلا العددين في صورة ذات الحدين، فيمكننا إجراء فحص سريع وسهل للغاية لمعرفة ما إذا كانا رقمين مركبين متساويين. ببساطة، يجب أن يتحقق التعبير التالي:
أ + ثنائية = أ + ثنائية
دعونا نرى مثالا، لتحديد ما إذا كان العددان المركبان التاليان متساويان:
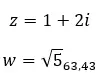
ربط الأعداد المركبة
لننتقل الآن إلى إحدى أهم خصائص الأعداد المركبة، لأن معرفة كيفية حساب مرافق المركب تساعدنا كثيرًا في حل عمليات القسمة المعقدة والتبسيط.
إذن من هاتين القيمتين:

نقول إنهما مترافقان إذا كانا يشتركان في وحدة نمطية ولديهما حجج متعارضة. ولذلك يجب استكماله:
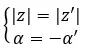
من ناحية أخرى، إذا كان لدينا كلا العددين في صورة ذات الحدين، فيمكننا إجراء فحص سريع وسهل للغاية لمعرفة ما إذا كانا رقمين مترافقين معقدين. ببساطة، يجب أن يتحقق التعبير التالي:
الأمم المتحدة + ثنائية = الأمم المتحدة – ثنائية
دعونا نرى مثالا، لتحديد ما إذا كان العددان المركبان التاليان مترافقين:
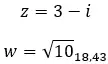
مقابل الأعداد المركبة
بعد ذلك، ننتقل لرؤية خاصية الأعداد المركبة المتقابلة. من هاتين القيمتين:

يمكننا القول أنهما متضادان إذا كان لهما نفس الوحدة وكانت وسيطاتهما تختلف بمقدار 180 درجة أو π راديان:
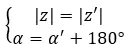
من ناحية أخرى، إذا كان لدينا كلا العددين في صورة ذات الحدين، فيمكننا استخدام طريقة أخرى أسرع وأبسط لمعرفة ما إذا كانا رقمين مركبين متقابلين. ببساطة، يجب أن يتحقق التعبير التالي:
أ + ثنائية = -أ – ثنائية
دعونا نرى مثالا، لتحديد ما إذا كان العددان المركبان التاليان متقابلين:
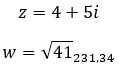
خصائص أخرى
من الواضح أن مجموعة الأرقام هذه لها خصائص أخرى، مثل الأعداد المركبة العكسية وبعض الخصائص الأخرى التي ترتبط ارتباطًا مباشرًا بالعمليات الحسابية الأساسية. على الرغم من أن كل هذا تم تناوله في مقالات أخرى، والتي يمكنك رؤيتها في القائمة أدناه.
تعرف على خصائص الأعداد المركبة
- ارقام مركبة
- العمليات على الأعداد المركبة
- جذور معقدة
- التمثيل البياني للأعداد المركبة