حساب نقطة التقاطع أو التقاطع بين خطين

ستجد هنا كيفية حساب نقطة القطع (أو التقاطع) بين خطين. سترى أيضًا أمثلة ويمكنك التدرب على حل التمارين خطوة بخطوة.

ما هي نقطة القطع أو التقاطع بين خطين؟

نقطة التقاطع (أو القطع) بين خطين هي النقطة التي يتقاطع فيها خطان مختلفان. لذلك، عندما يكون لخطين مختلفين تقاطع أو نقطة قطع، فهذا يعني أنهما يتطابقان عند نقطة واحدة.

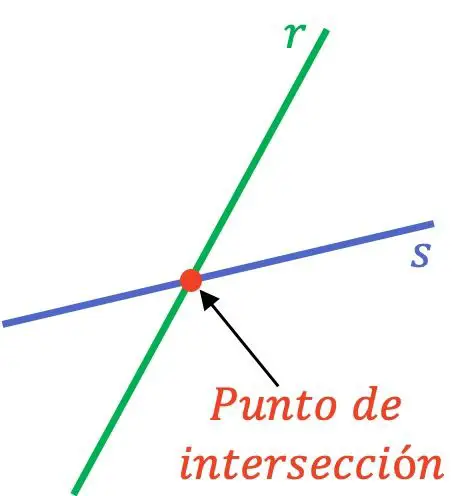
لكي يتقاطع خطان في نقطة ما، يجب أن يكونا خطين متقاطعين، لأن الخطوط المتوازية لا تتلامس في أي نقطة.

إذا كنت لا تتذكر بالضبط ما هي الخطوط المتقاطعة الآن، نوصي بمراجعة صفحة أمثلة الخطوط المتقاطعة ، حيث ستجد شرحًا تفصيليًا لماهية هذه الأنواع من الخطوط وكيفية معرفة ما إذا كان الخطان متقاطعين أم لا.

كيفية حساب نقطة القطع أو التقاطع بين خطين؟

بعد أن رأينا تعريف نقطة التقاطع أو التقاطع بين خطين، دعونا نرى الآن كيف يتم حساب النقطة المذكورة.

للعثور على نقطة التقاطع (أو التقاطع) بين خطين، يجب عليك أولاً التأكد من أن الخطين ليسا متوازيين، لأنه إذا كانا خطين متوازيين فلن يتقاطعا في أي نقطة. لذلك، عليك أولاً معرفة كيفية تحديد متى يكون الخطان متوازيين ومتى لا يكونان كذلك؛ إذا كنت لا تتذكر كيفية القيام بذلك، يمكنك مشاهدته مرة أخرى عن طريق النقر على الرابط.

وبمجرد أن عرفنا أن الخطين غير متوازيين، لتحديد نقطة التقاطع (أو التقاطع) بين الخطين، يجب علينا حل نظام المعادلات التي تتكون من معادلة كل خط. ونتيجة نظام المعادلات المذكور ستكون إحداثيات نقطة التقاطع (أو التقاطع) بين الخطين.

مثال لكيفية إيجاد نقطة التقاطع أو التقاطع بين خطين

على سبيل المثال، سنحل مشكلة حتى تتمكن من معرفة كيفية العثور على نقطة التقاطع (أو التقاطع) بين خطين:

أوجد نقطة التقاطع بين الخطين التاليين:

$r: \ y=4x-1 \qquad \qquad s: \ y=-2x+5$

أولًا، المستقيمان ليسا متوازيين؛ لأن ميليهما مختلفان، لذا فإنهما يتقاطعان عند نقطة على المستوى الديكارتي.

ولمعرفة ذلك يجب علينا حل نظام المعادلات المكون من معادلة كل سطر:

$\left. \begin{array}{l} y=4x-1 \\[2ex] y=-2x+5 \end{array} \right\}$

في هذه الحالة بالذات، سوف نقوم بحل النظام بطريقة المعادلة حيث المجهولين

$y$

تم حلها بالفعل (كلا الخطين في شكل معادلة صريحة):

$y= y$

$4x-1=-2x+5$

نقوم بحذف قيمة المتغير

$x:$

$4x+2x=5+1$

$6x=6$

$x = \cfrac{6}{6}$

$x = 1$

وبمجرد أن تعرف كم يستحق

$x,$

نعوض بقيمته في أي معادلة لإيجاد قيمته

$y:$

$y=4x-1 \ \xrightarrow{x \ = \ 1} \ y=4\cdot 1-1$

$y =4-1$

$y =3$

بحيث تكون إحداثيات نقطة التقاطع بين الخطين هي:

$\bm{(1,3)}$

حل مسائل نقطة التقاطع أو التقاطع بين خطين

التمرين 1

ما هي نقطة التقاطع أو التقاطع بين الخطين التاليين؟

$r: \ y=x+5 \qquad \qquad s: \ y=2x+3$

انظر الحل

أولًا، المستقيمان ليسا متوازيين؛ لأن ميليهما مختلفان، لذا سيلتقي الخطان في نقطة ما على المستوى.

لحساب النقطة المذكورة، من الضروري حل نظام المعادلات المكونة من معادلة كل سطر:

$\left. \begin{array}{l} y=x+5 \\[2ex] y=2x+3 \end{array} \right\}$

في هذه الحالة سوف نقوم بحل نظام المعادلات بطريقة المعادلة حيث المجهولين

$y$

تم حلها بالفعل (كلا الخطين في شكل معادلة صريحة):

$y= y$

$x+5=2x+3$

نقوم بحذف قيمة المتغير

$x:$

$x-2x=3-5$

$-x=-2$

$x=2$

وبمجرد أن تعرف كم يستحق

$x,$

نعوض بقيمته في أي معادلة لإيجاد قيمته

$y:$

$y=x+5 \ \xrightarrow{x \ = \ 2} \ y=2+5$

$y =7$

وبالتالي فإن إحداثيات نقطة التقاطع بين الخطين هي:

$\bm{(2,7)}$

تمرين 2

أوجد نقطة التقاطع أو التقاطع بين الخطين التاليين:

$r: \ y=-3x+1 \qquad \qquad s: \ 4x+2y+6=0$

انظر الحل

الحق

$s$

ويتم التعبير عنها على شكل معادلة ضمنية (أو عامة)، لذا سنمررها أولاً على شكل معادلة صريحة لمعرفة قيمة ميلها:

$4x+2y+6=0$

$2y=-4x-6$

$y=\cfrac{-4x-6}{2}$

$y=-2x-3$

إذن، كلا الخطين لهما ميلان مختلفان، وبالتالي توجد نقطة تقاطع بينهما.

لحساب النقطة المذكورة، من الضروري حل نظام المعادلات المكونة من معادلة كل سطر:

$\left. \begin{array}{l} y=-3x+1\\[2ex] y=-2x-3 \end{array} \right\}$

نحل نظام المعادلات بطريقة المعادلة:

$y= y$

$-3x+1=-2x-3$

نقوم بحذف قيمة المتغير

$x:$

$-3x+2x=-3-1$

$-x=-4$

$x=4$

وبمجرد أن تعرف كم يستحق

$x,$

نعوض بقيمته في أي من المعادلتين لإيجاد قيمة

$y:$

$y=-3x+1 \ \xrightarrow{x \ = \ 4} \ y=-3\cdot 4+1$

$y =-12+1$

$y =-11$

وبالتالي فإن إحداثيات نقطة التقاطع بين الخطين هي:

$\bm{(4,-11)}$

التمرين 3

حدد نقطة التقاطع أو التقاطع بين الخطين التاليين:

$\displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0$

انظر الحل

أولًا، علينا أن نعرف ما إذا كان هذان خطان متوازيان أم لا. للقيام بذلك، سنرى ما إذا كانت متجهات الاتجاه للخطين متناسبة.

الحق

$r$

يتم تعريفه على شكل معادلات بارامترية، وبالتالي فإن مكونات متجه اتجاهه هي المعاملات الموجودة أمام المعلمة

$t:$

$\vv{r} =(2,-3)$

ومن ناحية أخرى، الخط

$s$

يوصف في شكل معادلة ضمنية، وبالتالي فإن متجه اتجاهه هو:

$\vv{s} =(-B,A)=(-2,4)$

بحيث لا تتناسب مركبات متجهي الاتجاه مع بعضها البعض، وبالتالي فإن الخطين غير متوازيين.

$\cfrac{2}{-2} \neq \cfrac{-3}{4} \ \longrightarrow \ r \ \cancel{\parallel} \ s$

وبما أن الخطين غير متوازيين، فهذا يعني أن هناك بالفعل نقطة تقاطع بينهما. ولحسابها يجب علينا حل نظام المعادلات المكونة من معادلة كل سطر:

$\displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases} \qquad \qquad s: \ 4x+2y+8=0$

في هذه الحالة، مثل الخط

$r$

على شكل معادلات بارامترية، فمن الضروري استبدال تعبير كل معادلة بارامترية في معادلة الخط الآخر:

$4(1+2t)+2(-2-3t)+8=0$

الآن دعونا نحل المعادلة الناتجة:

$4+8t-4-6t+8=0$

$8t-6t=-8-4+4$

$2t=-8$

$t=\cfrac{-8}{2}$

$t=-4$

واستبدال قيمة

$t$

وجدت في المعادلات البارامترية للعثور على إحداثيات نقطة القطع:

$\displaystyle r: \ \begin{cases} x=1+2t \\[1.7ex] y=-2-3t \end{cases}$

$\begin{cases} x=1+2(-4)=1-8=-7 \\[1.7ex] y=-2-3(-4)=-2+12=10\end{cases}$

إذن نقطة التقاطع بين الخطين هي:

$\bm{(-7,10)}$

ما هي نقطة القطع أو التقاطع بين خطين؟

كيفية حساب نقطة القطع أو التقاطع بين خطين؟

مثال لكيفية إيجاد نقطة التقاطع أو التقاطع بين خطين

حل مسائل نقطة التقاطع أو التقاطع بين خطين

التمرين 1

تمرين 2

التمرين 3

اترك تعليقاً إلغاء الرد