الخطوط المتوازية

ستجد هنا كل ما يتعلق بالخطوط المتوازية: ماذا تعني، وكيفية تحديد ما إذا كان الخطان متوازيين، وخصائصهما، وما إلى ذلك. بالإضافة إلى ذلك، ستتمكن من رؤية العديد من الأمثلة والتدريبات المحلولة على الخطوط المتوازية.

ما هي الخطوط المتوازية؟

الخطوط المتوازية هي تلك الخطوط التي لا تتقاطع أبدًا، أي أنه حتى لو امتدت مساراتها إلى ما لا نهاية، فإنها لا تتلامس أبدًا. ولذلك، فإن نقاط الخطين المتوازيين تكون دائمًا على نفس المسافة من بعضها البعض، علاوة على ذلك، لا توجد نقاط مشتركة بين الخطين المتوازيين.

على سبيل المثال، الخطان التاليان متوازيان:

نشير بشكل عام إلى أن الخطين متوازيان مع شريطين عموديين || ما بين السطور

من ناحية أخرى، على الرغم من أن الخطين المتوازيين لا يتقاطعان أبدًا، إلا أننا في الهندسة التحليلية نقول إنهما يشكلان زاوية مقدارها 0 درجة لأن لهما نفس الاتجاه.

متى يكون الخطان متوازيين؟

بعد أن تعرفنا على تعريف الخطوط المتوازية، سنرى كيفية العثور على خطين متوازيين. من الواضح أن إحدى الطرق هي رسم الخطوط بيانيًا ومعرفة ما إذا كانت تتقاطع على الرسم البياني، ولكن هناك طرق أبسط وأسهل في الاستخدام.

تحديد توازي خطين مع ميليهما

يمكنك معرفة متى يكون الخطان متوازيين من خلال النظر إلى ميل كل خط. تذكر أن ميل الخط هو المعلمة

$m$

من المعادلة الصريحة ومعادلة نقطة الميل للخط:

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

ومع ذلك، هناك عدة طرق لتحديد ميل الخط، لذا لمعرفة كيفية حسابه، نوصي بإلقاء نظرة على صيغة ميل الخط . بالإضافة إلى ذلك، ستجد أيضًا في الصفحة المرتبطة شرحًا لما يمثله ميل الخط وسبب أهميته بالنسبة للخط.

وبالتالي، في المستوى، يكون الخطان متوازيين إذا كان لهما نفس الميل (المعامل m) وإحداثيات مختلفة عند نقطة الأصل (المعامل n) .

على سبيل المثال، الخطان التاليان متوازيان:

$r: \ y=5x+1 \qquad \qquad s: \ y=5x-3$

إنهما خطان متوازيان لأن كلاهما لهما نفس الميل، علاوة على ذلك، فإن حديهما المستقلين مختلفان.

$m_r =m_s =5$

$n_r =1 \neq n_s =-3$

تجدر الإشارة إلى أنه إذا كان لخطين نفس الميل وفي نفس الوقت نفس الكمبيوتر عند نقطة الأصل، فسيكونان خطين متطابقين لأنهما سيكونان متطابقين تمامًا.

أوجد توازي خطين من المعادلة الضمنية

تذكر أن المعادلة الضمنية (أو العامة) للخط هي:

$Ax+By+C=0$

وبالتالي، إذا كان المعاملان A و B لخطين متناسبين مع بعضهما البعض ولكن ليس مع المعامل C ، فهذا يعني أن الخطين متوازيان.

$r: \ Ax+By+C=0 \qquad \qquad s: \ A'x+B'y+C'=0$

$\cfrac{A}{A'} = \cfrac{B}{B'} \neq \cfrac{C}{C'} \quad \bm{\longrightarrow} \quad r \parallel s$

فيما يلي خطان متوازيان يتم التعبير عنهما بصيغة معادلة عامة (أو ضمنية):

$r: \ 4x-6y+7=0 \qquad \qquad s: \ -2x+3y-1=0$

إنهما متوازيان لأن الأرقام الموجودة أمام المتغير

$x$

تتناسب مع الأرقام الموجودة أمام المتغير

$y$

ولكن ليس بشروط مستقلة.

$\cfrac{4}{-2} = \cfrac{-6}{3} = -2 \neq \cfrac{7}{-1}=-7$

كما كان من قبل، إذا كانت جميع المعاملات (A، B، C) لخطين ضمنيين متناسبة، فإن هذا يعني أن الخطين متطابقان، أو بمعنى آخر، أنهما متساويان.

خصائص الخطوط المتوازية

خصائص الخطوط المتوازية هي كما يلي:

خاصية التماثل : إذا كان أحد المستقيمين موازيا لآخر، فإن هذا الخط موازي للأول أيضا. تمتلك هذه الخاصية أيضًا الخطوط المتعامدة.

$r \parallel s \ \longrightarrow \ s \parallel r$

خاصية متعدية : إذا كان مستقيم موازيا لخط آخر، وهذا الخط الثاني موازي لخط ثالث، فإن السطر الأول موازي للسطر الثالث أيضا.

$\left. \begin{array}{c} r \parallel s\\[2ex] s \parallel q \end{array} \right\} \longrightarrow \ r \parallel q$

المنتج العددي لمتجهات الاتجاه (المتجه الذي يشير إلى اتجاه الخط) لخطين متوازيين يساوي منتج وحداتهما.

$r \parallel s \ \longrightarrow \ \vv{\text{v}}_r \cdot \vv{\text{v}}_s= \lvert \vv{\text{v}}_r \rvert \cdot \lvert \vv{\text{v}}_s \rvert$

علاوة على ذلك، فإن متجهات الاتجاه لخطين متوازيين تعتمد دائمًا خطيًا على بعضها البعض، لأنها متناسبة .

هذا الشرط ضروري لكي تكون الخطوط متوازية ولكنها غير كافية، أو بمعنى آخر، يجب أن يكون للخطين المتوازيين متجهات اتجاه متناسبة، لكن حقيقة أن الخطين لهما متجهات اتجاه متناسبة لا تعني بشكل مباشر أنهما متوازيان. نظرًا لأن الخطوط المتزامنة لها أيضًا متجهات اتجاه متناسبة.

الخطوط الموازية لمحور الإحداثي السيني (المحور X) تكون أفقية ولها الشكل دائمًا
$y=k.$

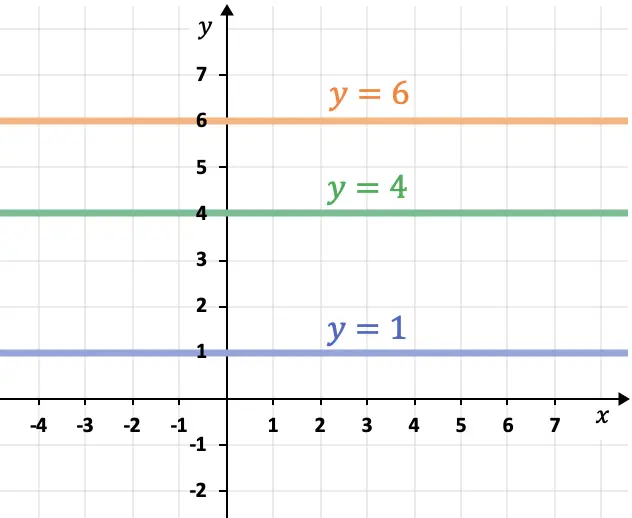
الخطوط الموازية لمحور الكمبيوتر (المحور Y) تكون عمودية وتتبع التعبير دائمًا
$x=k.$

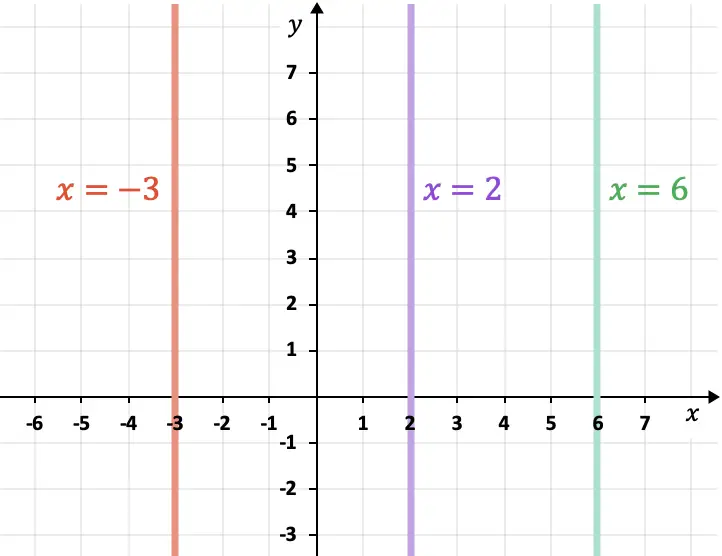
كيفية حساب المسافة بين خطين متوازيين في المستوى

للعثور على المسافة بين خطين متوازيين في المستوى (في R2)، ما عليك سوى أخذ نقطة على أحد الخطين وحساب المسافة من هذه النقطة إلى الخط الآخر.

يمكننا فعل ذلك بهذه الطريقة لأن الخطين المتوازيين يفصل بينهما دائمًا نفس المسافة.

من ناحية أخرى، إذا حصلنا عند استخدام الصيغة على مسافة 0 وحدة، فهذا يعني أن الخطوط تلامس بعضها البعض في نقطة ما، وبالتالي فإن الخطوط ليست متوازية، ولكنها متقاطعة أو متطابقة أو متعامدة. إذا أردت، يمكنك التحقق من الاختلافات بين هذا النوع من الخطوط على موقعنا.

لذا، حتى تتمكن من رؤية كيفية القيام بذلك، سوف نحدد المسافة بين الخطين المتوازيين التاليين كمثال:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

أول شيء يتعين علينا القيام به هو الحصول على نقطة على أحد الخطوط (الخط الذي تريده). في هذه الحالة، سوف نقوم بحساب نقطة على الخط

$s.$

للقيام بذلك، يجب علينا إعطاء قيمة لأحد المتغيرات، سنفعل على سبيل المثال

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

والآن نقوم بمسح المتغير الآخر (

$y$

) من المعادلة التي تم الحصول عليها لمعرفة كم قيمتها في هذه المرحلة:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

ولذلك، فإن النقطة التي تم الحصول عليها من الخط

$s$

شرق:

$P(0,-2)$

وبمجرد أن يكون لدينا بالفعل نقطة على الخط، فإننا نحسب المسافة من تلك النقطة إلى الخط الآخر باستخدام صيغة المسافة من نقطة إلى خط:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{\lvert 0+8-6\rvert}{\sqrt{4+16}}={\cfrac{2}{\sqrt{20}}=\bm{0,45}$

وبالتالي فإن المسافة بين الخطين المتوازيين تعادل 0.45 وحدة .

الخطوط المتوازية حل المشاكل

التمرين 1

أي الخطوط التالية متوازي؟

$\begin{array}{l} r: \ y=2x+3 \\[2ex] s: \ y=3x-2 \\[2ex] q: \ y=2x+6 \\[2ex] t: \ y=-2x-4\end{array}$

انظر الحل

يكون الخطان متوازيين إذا كان لهما نفس الميل (وتقاطعات مختلفة). وبالتالي فإن ميل كل خط هو:

$m_r = 2$

$m_s = 3$

$m_q = 2$

$m_t = -2$

إذن الخطوط فقط هي المتوازية

$r$

$q,$

لأنهما الوحيدان اللذان لديهما ميلان متساويان.

تمرين 2

أوجد المعادلة الصريحة للمستقيم الموازي للخط

$r$

وماذا يحدث عبر هذه النقطة

$P(0,2).$

ليكون مستقيما

$r:$

$r: \; y=3x-1$

انظر الحل

بحيث يكون الخط موازيا للخط

$r,$

كلاهما يجب أن يكون لهما نفس المنحدر. ومنحدر الخط

$r$

هو 3:

$m = 3$

وبالتالي، فإن المعادلة الصريحة للخط الذي نحتاج إلى إيجاده ستكون:

$y=3x+n$

وبمجرد أن نعرف ميل الخط، يمكننا حساب التقاطع عن طريق تعويض النقطة التي تنتمي إلى الخط في معادلة الخط:

$P(0,2)$

$y= 3x+n \ \xrightarrow{x=0 \ ; \ y=2} \ 2=3\cdot 0 +n$

$2=0+ n$

$2= n$

وبالتالي فإن المعادلة الصريحة للخط هي:

$\bm{y=3x+2}$

التمرين 3

احسب قيمة المجهول

$a$

$b$

بحيث يكون الخطان التاليان متوازيين:

$r: \ 2x-4y+6=0 \qquad \qquad s: \ x+ay+b=0$

انظر الحل

يتم وصف الخطوط في شكل معادلة عامة (أو ضمنية). ولذلك، لكي يكون الخطان متوازيين، يجب أن يكون معاملاهما A وB متناسبين، أي يجب تحقيق المعادلة التالية:

$\cfrac{2}{1} = \cfrac{-4}{a}$

ولذلك يجب علينا حل المعادلة السابقة للحصول على قيمة المجهول

$a.$

للقيام بذلك، نقوم بضرب الكسور بالعرض:

$2 \cdot a = -4 \cdot 1$

$a = \cfrac{-4}{2}$

$\bm{a=-2}$

من ناحية أخرى، لكي تكون الخطوط متوازية، لا يمكن أن تكون حدودها المستقلة متناسبة مع المعاملات الأخرى:

$\cfrac{2}{1} \neq \cfrac{6}{b}$

لذلك، كما في السابق، نحل المتباينة عن طريق ضرب الكسور بالعرض:

$2 \cdot b \neq 6 \cdot 1$

$b \neq \cfrac{6}{2}$

$\bm{b\neq 3}$

باختصار، بحيث يكون الخطان متوازيين

$a$

يجب أن يكون 2 و

$b$

يمكن أن يكون أي عدد حقيقي باستثناء 3.

التمرين 4

ما المسافة بين الخطين المتوازيين التاليين؟

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

انظر الحل

أولاً، سوف نتحقق من أن هذين الخطين متوازيان. لهذا، معاملات المتغيرات

$x$

$y$

يجب أن تكون متناسبة مع بعضها البعض ولكن ليس مع الشروط المستقلة:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

في الواقع، الخطوط متوازية، وبالتالي يمكننا تطبيق الإجراء.

الآن نحن بحاجة للحصول على نقطة من أحد الخطوط (الخط الذي تريده). في هذه الحالة، سوف نقوم بحساب نقطة على الخط

$s.$

للقيام بذلك، يجب عليك تعيين قيمة لأحد المتغيرات، على سبيل المثال سنفعل

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

والآن نقوم بمسح المتغير الآخر (

$y$

) للمعادلة التي تم الحصول عليها لمعرفة قيمتها عند هذه النقطة:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

بحيث يتم الحصول على النقطة من السطر

$s$

شرق:

$P(0,-1)$

بمجرد أن نعرف نقطة على الخط، نحسب المسافة من تلك النقطة إلى الخط الآخر بالصيغة:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

ما هي الخطوط المتوازية؟

متى يكون الخطان متوازيين؟

تحديد توازي خطين مع ميليهما

أوجد توازي خطين من المعادلة الضمنية

خصائص الخطوط المتوازية

كيفية حساب المسافة بين خطين متوازيين في المستوى

الخطوط المتوازية حل المشاكل

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد