ستجد في هذه الصفحة شرحا عن الطائرة وكيفية حسابها وجميع خصائصها. بالإضافة إلى ذلك، ستتمكن من رؤية أمثلة للمستويات، وما هي المواضع النسبية بين مستويين، وكيفية تحديد الزاوية بين مستويين، وأخيرًا، كيفية التعبير عن أي مستوى عدديًا باستخدام معادلات المستوى.
ما هي الخطة؟
وفي الهندسة التحليلية يكون تعريف المستوى كما يلي:
المستوى هو جسم هندسي له بعدين (الطول والعرض).
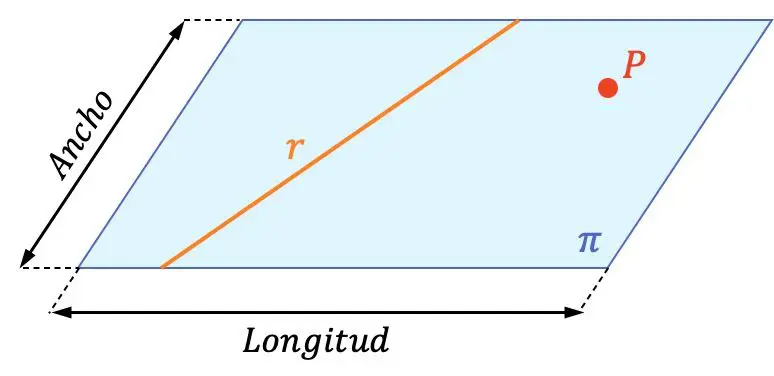
ولذلك، فإن المستوى يحتوي على خطوط لا نهاية لها ونقاط لا نهاية لها. في التمثيل البياني أعلاه يمكنك رؤية الفرق بين المستوى والخط والنقطة. يمكنك أيضًا التحقق من أن الخط
![]()
والطرف
![]()
موجودة في الطائرة
![]()
كما ترون في المخطط البياني، تتم تسمية الخطط عادةً بأحرف يونانية:
![]()
مثال على المستوى الذي نستخدمه كثيرًا في الرياضيات هو المستوى الديكارتي. المستوى الديكارتي هو المستوى المحدد بواسطة محور الإحداثي (المحور X) والمحور الإحداثي (المحور Y). أحد استخدامات المستوى الديكارتي هو أنه يستخدم لوصف موضع جسم ما في نظام مرجعي.
تحديد خطة
الآن بعد أن رأينا معنى المستوى، دعونا نرى كيف يمكن تحديد أي مستوى في الفضاء ثلاثي الأبعاد (في R3).
يتم تحديد المخطط بالكامل من خلال العناصر الهندسية التالية:
- ثلاث نقاط غير محاذاة.
- خط مستقيم ونقطة خارجه.
- خطان متوازيان أو خطان متقاطعان.
فيما يتعلق بالنقطة الأخيرة، ربما تعرف بالفعل ما يعنيه أن يكون الخطان متوازيين. لكن معنى الخطوط القاطعة أقل شهرة، لذا إذا كانت لديك أي أسئلة هنا، يمكنك التحقق من الخطوط القاطعة .
ولذلك، إذا كان لدينا أي من الشروط الثلاثة السابقة، فهذا يعني أنه يمكننا وضع خطة.
خصائص الخطة
تتمتع الخطة بالخصائص التالية:
- يحتوي المستوى على عدد لا نهائي من النقاط.
- يحتوي المستوى على عدد لا نهائي من الخطوط.
- والمستوى غير محدود، أي أنه سطح يمتد في الفضاء بلا حدود.
- طائرتان متقاطعتان تحددان الخط.
- الخط الذي له نقطة في المستوى ليس بالضرورة موجودًا هناك. لكي يكون الخط جزءًا من المستوى، يجب أن يحتوي على نقطتين على الأقل في المستوى.
- الطائرات اللانهائية تعبر خطًا مستقيمًا.
- نصف المستوى هو كل جزء من الجزأين اللذين ينقسم إليهما المستوى عند قطعه بأحد خطوطه.
معادلات الطائرة
في الهندسة التحليلية، معادلة المستوى هي معادلة تسمح بالتعبير عن أي مستوى رياضيًا. لذا، لإيجاد معادلة المستوى، فإنك تحتاج فقط إلى نقطة ومتجهين مستقلين خطيًا ينتميان إلى ذلك المستوى.

ومع ذلك، كما رأينا أعلاه في شرح مفهوم الخطة، هناك عدة طرق لتحديد الخطة. حسنًا، بنفس الطريقة، هناك أيضًا طرق مختلفة للتعبير عن الخطة تحليليًا.
وبالتالي فإن جميع أنواع معادلات المستوى هي: المعادلة المتجهة ، والمعادلات البارامترية ، والمعادلة الضمنية (أو العامة) والمعادلة القانونية (أو القطاعية) للمستوى.
ثم سنرى بالتفصيل شرح وصيغة جميع معادلات الخطة.
معادلة المتجهات للطائرة
خذ بعين الاعتبار النقطة ومتجهي الاتجاه للمستوى:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
صيغة المعادلة المتجهة للمستوى هي:
![]()
أو ما يعادلها:
![]()
ذهب
![]()
و
![]()
هما عددان قياسيان، أي عددان حقيقيان.
المعادلات البارامترية للطائرة
صيغة المعادلة البارامترية للمستوى هي:
![]()
ذهب:
-
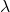
و
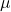
هما عددان قياسيان، أي عددان حقيقيان.
-
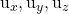
هي مكونات أحد الموجهين الموجهين للخطة
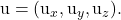
-
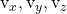
هي مكونات ناقل التوجيه الآخر للخطة
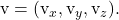
المعادلة الضمنية أو العامة للطائرة
خذ بعين الاعتبار النقطة ومتجهي الاتجاه للمستوى:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
يتم الحصول على المعادلة الضمنية أو العامة أو الديكارتية للمستوى عن طريق حل المحدد التالي وجعل النتيجة تساوي 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
وبذلك تكون المعادلة الضمنية أو العامة للخطة الناتجة كما يلي:
![]()
ويسمى هذا النوع من المعادلات المستوية أيضًا معادلة المستوي الديكارتي.
المعادلة الكنسي أو القطعي للطائرة
صيغة المعادلة الأساسية أو القطاعية للمستوى هي كما يلي:
![]()
ذهب:
-

هي نقطة التقاطع بين المستوى والمحور X.
-

هي نقطة التقاطع بين المستوى والمحور Y.
-

هذا هو المكان الذي يتقاطع فيه المستوى مع المحور Z.
يمكن أيضًا الحصول على المعادلة الأساسية (أو المعادلة القطاعية) للمستوى من معادلتها العامة:
![]()
أولاً نحل المعامل D من المعادلة:
![]()
ثم نقسم معادلة الخطة بأكملها على قيمة المعلمة D المتغيرة:
![]()
![]()
وباستخدام خصائص الكسور نصل إلى التعبير التالي:
![]()
لذلك نستنتج من هذا التعبير الصيغ التي تسمح بحساب شروط المعادلة الأساسية أو القطاعية للمستوى بشكل مباشر:
![]()
وبالتالي، لكي نتمكن من تكوين هذا البديل لمعادلات الخطة، يجب أن تكون المعاملات A وB وC مختلفة عن الصفر، وبالتالي تجنب عدم تحديد الكسور.
الموقع النسبي لطائرتين
في الهندسة التحليلية، هناك ثلاثة مواضع نسبية محتملة فقط بين مستويين: المستويات القاطعة، والمستويات المتوازية، والمستويات المتطابقة.
- المستويات المتقاطعة : يتقاطع المستويان إذا تقاطعا على خط واحد فقط.
- المستويان المتوازيان : يكون المستويان متوازيين إذا لم يتقاطعا في أي نقطة.
- المستويان المتطابقان : تكون المستويتان متطابقتين إذا كانت بينهما نقاط مشتركة.
طائرات متقاطعة

طائرات متوازية

طائرات متزامنة

بالإضافة إلى ذلك، إذا تقاطع مستويان متقاطعان بزاوية 90 درجة، فإنهما يكونان مستويين متعامدين بشكل متبادل .
الزاوية بين طائرتين
الزاوية بين طائرتين تساوي الزاوية التي تشكلها المتجهات العادية للطائرات المذكورة. ولذلك، لإيجاد الزاوية بين مستويين، يتم حساب الزاوية التي تشكلها متجهاتها العادية، لأنها متكافئة.
لذلك، بمجرد أن نعرف بالضبط مما تتكون الزاوية بين مستويين، دعونا نرى صيغة حساب الزاوية بين مستويين في الفضاء، والتي يتم استنتاجها من صيغة الزاوية بين متجهين:
بالنظر إلى المعادلة العامة (أو الضمنية) لطائرتين مختلفتين:
![]()
![]()
المتجه الطبيعي لكل مستوى هو :
![]()
![]()
ويتم تحديد الزاوية التي تشكلها هاتان المستويتان من خلال حساب الزاوية التي تشكلها متجهاتها العادية باستخدام الصيغة التالية:
![]()
من الواضح أنه بمجرد أن نحسب جيب تمام الزاوية التي تشكلها المستويتان من الصيغة، يجب علينا عكس جيب التمام للعثور على قيمة الزاوية المذكورة.
من ناحية أخرى، عندما يكون المستويان متعامدين أو متوازيين، ليس من الضروري تطبيق الصيغة، لأنه يمكن تحديد الزاوية بين المستويين مباشرة:
- الزاوية بين مستويين متوازيين هي 0 درجة، لأن متجهاتهما العادية لها نفس الاتجاه.
- الزاوية بين مستويين متعامدين هي 90 درجة، لأن متجهاتها العادية متعامدة أيضًا (أو متعامدة) مع بعضها البعض، وبالتالي تشكل زاوية قائمة.