شرح لكيفية حساب معادلة المستوى الضمني (الصيغة)، والمعروفة أيضًا بالمعادلة العامة أو الديكارتية. بالإضافة إلى ذلك، ستجد كيفية العثور على معادلة المستوى من متجهه الطبيعي. والأكثر من ذلك، أنك ستتمكن من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة.
ما هي المعادلة الضمنية أو العامة للخطة؟
في الهندسة التحليلية، المعادلة الضمنية للمستوى ، وتسمى أيضًا المعادلة العامة أو الديكارتية للمستوى، هي معادلة تسمح بالتعبير عن أي مستوى رياضيًا. لإيجاد المعادلة الضمنية أو العامة للمستوى، نحتاج إلى نقطة ومتجهين مستقلين خطيًا ينتميان إلى ذلك المستوى.
صيغة المعادلة الضمنية أو العامة للخطة
خذ بعين الاعتبار النقطة ومتجهي الاتجاه للمستوى:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
يتم الحصول على المعادلة الضمنية أو العامة أو الديكارتية للمستوى عن طريق حل المحدد التالي وجعل النتيجة تساوي 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
وبذلك تكون المعادلة الضمنية أو العامة للخطة الناتجة كما يلي:
![]()
من المهم أن يكون المتجهان في الصيغة مستقلين خطيًا عن بعضهما البعض، أي أنه يجب أن يكون لهما اتجاهات مختلفة. ويكفي لتحقيق هذا الشرط ألا يكون المتجهان متوازيين.

على الرغم من أنه ليس من الضروري معرفة سبب هذه الصيغة، يمكنك رؤية العرض التوضيحي لها أدناه.
بدءًا من المعادلات البارامترية للخطة، سننتقل إلى المعادلة الضمنية (أو العامة) للخطة:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-46f87775f11f01a59c70aa3ee864aebe_l3.png)
أولاً، نقوم بتمرير الحد المستقل من كل معادلة بارامترية إلى الطرف الآخر من المعادلة:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases}x-P_x= \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y-P_y = \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z-P_z = \lambda\text{u}_z + \mu \text{v}_z \end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-0c2f3831ca03939d7e23d24c7d435337_l3.png)
أو ما يعادلها:
![Rendered by QuickLaTeX.com \displaystyle \begin{cases} \lambda \text{u}_x + \mu \text{v}_x =x-P_x\\[1.7ex] \lambda \text{u}_y + \mu \text{v}_y=y-P_y \\[1.7ex] \lambda\text{u}_z + \mu \text{v}_z =z-P_z\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-aca0b16ff9b92401181c2bdc5ba981bf_l3.png)
لكي يكون لنظام المعادلات أعلاه حل ممكن، يجب أن تكون رتبة المصفوفة التالية مساوية لـ 2 (نظرية روش-فروبينيوس):
![Rendered by QuickLaTeX.com \displaystyle\begin{pmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6f802b760ba5ab681afd0f02c83eddb6_l3.png)
لذا، إذا كان مدى المصفوفة السابقة يجب أن يكون اثنين، فإن المحدد 3×3 يجب أن يكون بالضرورة مساويًا للصفر:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
وبحل هذا المحدد نحصل على المعادلة العامة أو الضمنية أو الديكارتية للمستوى:
![]()
لقد رأينا للتو المعادلة الضمنية (أو العامة) والمعادلات البارامترية للمستوى، ومع ذلك، هناك المزيد من الطرق للتعبير عن المستوى تحليليًا، مثل المعادلة المتجهة والمعادلة الأساسية. يمكنك الاطلاع على الصيغة وشرح جميع المعادلات الموجودة في الخطة في هذا الرابط.
مثال لكيفية إيجاد المعادلة الضمنية أو العامة للمستوى
دعونا نرى كيفية تحديد المعادلة الضمنية (أو العامة أو الديكارتية) للمستوى من خلال مثال:
- أوجد المعادلة الضمنية أو العامة للمستوى الذي يمر بالنقطة
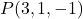
ويحتوي على المتجهات
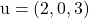
و
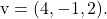
لحساب المعادلة العامة أو الضمنية للمستوى، من الضروري حل المحدد التالي المكون من المتجهين والمتغيرات وإحداثيات النقطة:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
لذا، نعوض بالمتجهات والنقطة في الصيغة:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z-(-1) \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-aa25223c3a00e31f89043a3500d32c68_l3.png)
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}2 & 4 & x-3 \\[1.1ex]0 & -1 & y-1 \\[1.1ex]3& 2 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-7886f1c2758c204802b96f44acc8a7cd_l3.png)
والآن نحل محدد الترتيب 3، على سبيل المثال مع قاعدة ساروس أو العوامل المساعدة (أو النواب):
![]()
الآن نعمل ونجمع المصطلحات:
![]()
![]()
![]()
ولذلك فإن المعادلة الضمنية أو العامة للخطة هي:
![]()
احسب المعادلة الضمنية أو العامة للمستوى من متجهه الطبيعي
إحدى المشاكل النموذجية في معادلات المستوى هي إيجاد الشكل الذي تبدو عليه معادلة مستوى معين بمعلومية نقطة ومتجهها الطبيعي (أو المتعامد). لذلك، دعونا نرى كيف يعمل.
لكن يجب أن تعلم أولاً أن المكونات X وY وZ للمتجه الطبيعي للمستوى تتطابق على التوالي مع المعاملات A وB وC للمعادلة الضمنية (أو العامة) للمستوى المذكور.
![]()
ذهب
![]()
هو المتجه المتعامد على المستوى
![]()
بعد أن عرفنا العلاقة السابقة، دعونا نرى مثالاً لحل هذا النوع من مسائل المعادلات المستوية:
- حدد المعادلة الضمنية أو العامة للمستوى الذي يمر بالنقطة
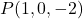
وأحد ناقلاته العادية هو
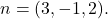
صيغة المعادلة الضمنية أو العامة أو الديكارتية للمستوى هي:
![]()
وهكذا، من المتجه العادي يمكننا إيجاد المعاملات A وB وC لأنها تعادل مكونات متجهه الطبيعي:
![]()
بينما نحتاج فقط إلى إيجاد المعلمة D. وللقيام بذلك، نعوض بإحداثيات النقطة التي تنتمي إلى المستوى في المعادلة:
![]()
![]()
![]()
![]()
![]()
وبالتالي فإن المعادلة الضمنية أو العامة للخطة هي:
![]()
حل مسائل المعادلة الضمنية أو العامة للطائرة
التمرين 1
أوجد المعادلة الضمنية أو العامة للمستوى الذي يمر بالنقطة
![]()
ويحتوي على المتجهات
![]()
و
![]()
لحساب المعادلة العامة أو الضمنية للمستوى، من الضروري حل المحدد التالي المكون من المتجهين والمتغيرات الثلاثة وإحداثيات النقطة:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
لذا، نعوض بالمتجهات والنقطة في الصيغة:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}4 & 5 & x+2 \\[1.1ex]1 & 3 & y-1 \\[1.1ex]3& 1 & z+1 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-02e103601cd9992a8a8c087d016a08c1_l3.png)
والآن نحل محدد المصفوفة 3×3 بالطريقة التي تختارها:
![]()
أخيرًا، نقوم بتنفيذ العمليات وتجميع المصطلحات المتشابهة:
![]()
![]()
![]()
وبالتالي فإن المعادلة الضمنية أو العامة للخطة هي:
![]()
تمرين 2
تحديد ما إذا كانت النقطة
![]()
ينتمي إلى الخطة التالية:
![]()
ولكي تكون النقطة في المستوى يجب التحقق من معادلتها. لذلك، نحتاج إلى استبدال الإحداثيات الديكارتية للنقطة في معادلة المستوى والتحقق من استيفاء المعادلة:
![]()
![]()
![]()
![]()
![]()
النقطة لا تحترم معادلة المستوى، لذا فهي ليست جزءًا من هذا المستوى.
التمرين 3
أوجد المعادلة الضمنية (أو العامة) للخطة التي تحتوي على النقاط الثلاث التالية:
![]()
لإيجاد المعادلة الضمنية للمستوى، علينا إيجاد متجهين مستقلين خطيًا يرتبطان في المستوى. ولهذا يمكننا حساب متجهين محددين بالنقاط الثلاث:
![]()
![]()
إحداثيات المتجهين الموجودين غير متناسبة، لذا فهما مستقلان خطيًا عن بعضهما البعض.
الآن نحن نعرف بالفعل متجهي اتجاه ونقطة واحدة من المستوى، لذا يمكننا بالفعل تطبيق صيغة المعادلة العامة للمستوى:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-917f1770ff2a17897e5df76998ec3519_l3.png)
نعوض بالمتجهات وإحدى النقاط الثلاث في الصيغة:
![Rendered by QuickLaTeX.com \displaystyle\begin{vmatrix}-3 & -1 & x-5 \\[1.1ex]2 & 2 & y+1 \\[1.1ex]5& 0 & z+2 \end{vmatrix} =0](https://mathority.org/wp-content/ql-cache/quicklatex.com-383093e607bc8ecc5f99e1815242b22a_l3.png)
وأخيرا، نحل المحدد:
![]()
![]()
![]()
![]()
وباختصار، فإن المعادلة الضمنية أو العامة أو الديكارتية للمستوى المعني هي:
![]()
التمرين 4
حساب المعادلة الضمنية أو العامة للمستوى في الفضاء الذي يمر عبر النقطة
![]()
وأحد ناقلاته العادية هو
![]()
صيغة المعادلة الضمنية أو العامة أو الديكارتية للمستوى هي:
![]()
حسنًا، من المتجه العادي يمكننا إيجاد المعاملات A وB وC، لأنها تساوي على التوالي مكونات المتجه العادي:
![]()
لذلك نحتاج فقط إلى إيجاد المعلمة D. وللقيام بذلك، نعوض بإحداثيات النقطة التي تنتمي إلى المستوى في المعادلة:
![]()
![]()
![]()
![]()
![]()
وفي الختام فإن المعادلة الضمنية أو العامة للخطة هي:
![]()