المعادلة التربيعية أو المعادلة التربيعية هي معادلة من الدرجة 2، حيث يكون الأس الأكبر لأحد حدودها يساوي 2. وهذا يعني أن المعادلة يمكن أن يكون لها ما يصل إلى حلين مختلفين، على الرغم من أنها قد يكون لها أيضًا حل فريد أو لاشيء على الاطلاق.
لحساب حلول أو جذور المعادلات التربيعية، يمكننا اتباع إجراءين مختلفين: عن طريق الصيغة التربيعية أو عن طريق تحليل التعبير . في هذا المقال سنتحدث عن كلتا الطريقتين وسنقدم لك بعض التمارين العملية. على الرغم من أننا سنقوم قبل ذلك بتوضيح بعض المفاهيم حتى يكون الشرح بأكمله مفهومًا جيدًا وتحصل على أقصى استفادة من القراءة.
أنواع المعادلات التربيعية
يعتمد التصنيف الرئيسي بين المعادلات التربيعية على بنية التعبير نفسه. وبالتالي فإن البنية القياسية أو المعتادة لهذه التعبيرات هي كما يلي: ax² + bx + c . هذا النموذج الشائع يعادل معادلة كاملة، ولكن عندما تكون هناك حدود فارغة أو فارغة، فيمكن أن يختلف الهيكل، وهنا تظهر المعادلات غير المكتملة. وبعد ذلك سنشرح خصائص جميع الأنواع بمزيد من التفصيل.
المعادلات التربيعية كاملة
كما قلنا سابقًا، لدينا المعادلات التربيعية الكاملة ، وجميع معاملاتها a وb وc غير صفرية. وبالتالي يتبع التعبير البنية ax² + bx + c حرفيًا، لأنه يحتوي على جميع المصطلحات: الحد التربيعي، والحد الخطي، والحد المستقل. مثال على هذا النوع المعادلة التالية: x² + 2x + 1 = 0.
المعادلات التربيعية غير الكاملة
أما المعادلات غير الكاملة فيمكننا تمييزها من خلال معاملها يساوي الصفر. تذكر أنه إذا لم يحل هذا الشرح شكوكك، فستجد أدناه صورة يمكنك من خلالها العثور على جميع الحالات مشروحة خطوة بخطوة.
- المعادلات غير الكاملة (ب = 0): في هذه الحالة الأولى نجد تعبيراً يتبع البنية التالية: ax² + c = 0. وبهذا نحصل على نتيجتين: سالب وموجب جذر الكسر c/a .
- المعادلات غير الكاملة (ج = 0): عندما يكون لدينا الصيغة ax² + bx = 0 يجب علينا تحليل المعادلة للحصول على التعبير x (ax + b) = 0. لذلك سيكون لدينا حلان: x = 0 و x = – ب / أ.
- المعادلات غير الكاملة (ب = ج = 0): في هذه الحالة لدينا معادلة ax² = 0 ولدينا حل واحد ممكن فقط، وهو x = 0.
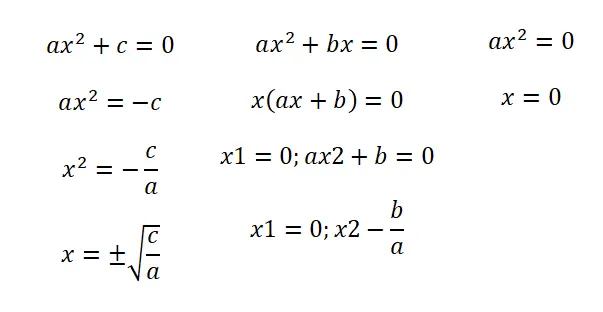
ومن الجدير بالذكر أن الإجراءات التي علمناها لك تتيح لك التحرك بشكل أسرع عند حل المعادلات غير المكتملة. لكن في كل الأحوال يمكنك استخدام الصيغة التربيعية التي سنعلمك إياها أدناه، كل ما عليك فعله هو كتابة صفر في المعاملات غير الموجودة.
صيغة المعادلات التربيعية
لحل المعادلات التربيعية (ax² + bx + c = 0)، نحتاج إلى تطبيق الصيغة العامة أو الصيغة التربيعية ثم نحتاج إلى استبدال القيم العددية التي تتوافق مع كل حرف في التعبير الرياضي.
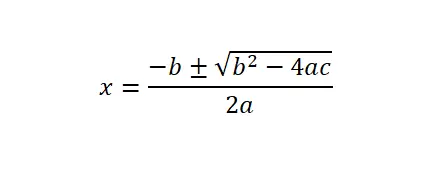
ومن المهم أيضًا توضيح أن المميز (Δ) هو التعبير b² – 4ac، الموجود تحت الجذر التربيعي. ومن هذا المفهوم الرياضي يمكننا معرفة عدد الحلول لهذه المعادلة التربيعية. في الأساس، هناك ثلاثة خيارات: المميز سالب (لا توجد حلول حقيقية)، المميز صفر (يوجد حل واحد فقط)، أو المميز موجب (يوجد له حلان).
مثال على حل المعادلة التربيعية الكاملة
حاول حل المعادلة التربيعية التالية: 2x²+4x-6=0 وتحقق من نتيجتك باستخدام المعادلة أدناه. ننصحك باتباع الإجراء التالي: تحليل نوع المعادلة (تحديد الحدود الصفرية)، وحساب المميز لمعرفة عدد الحلول الموجودة، وأخيراً حل المعادلة المقترحة بالصيغة.
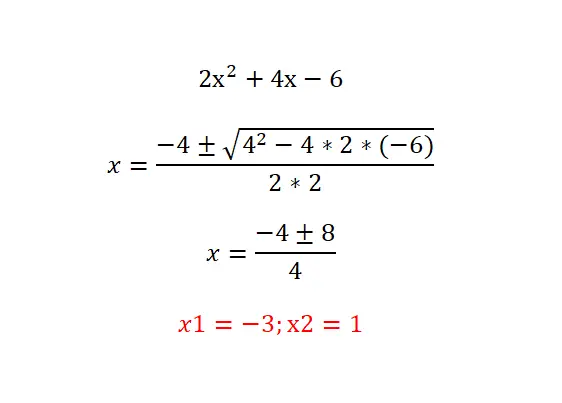
المعادلات التربيعية العاملية
الطريقة الثانية لحل المعادلات التربيعية هي التحليل . لذا، لتحليل كثيرة الحدود (في حالتنا كثيرة الحدود التربيعية)، يمكننا استخدام طرق مختلفة. على الرغم من أنه بشكل عام، عندما يتعلق الأمر بالمعادلات من هذا النمط، فإنها عادة ما تكون قابلة للتحليل بمصطلح مشترك. وإذا لم يكن الأمر كذلك، فيمكنك تجربة تطبيق الهويات البارزة ، ولكن عادةً لن تحتاج إلى معرفة أي طرق أخرى في هذه المواقف.
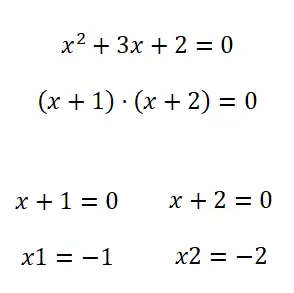
تمارين على المعادلات التربيعية مع الحلول
ستجد أدناه سلسلة من التمارين حول المعادلات التربيعية الكاملة وغير الكاملة . بهذه الطريقة ستراجع جميع النظريات الموضحة خلال هذه المقالة وسيكون من الواضح لك كيفية تطبيقها في التمارين. ننصحك بمحاولة حلها بنفسك وعدم النظر إلى الحل إلا عند الانتهاء منها أو عندما تتعثر. ومع ذلك، يمكنك البدء في حل التمارين الآن.
التمرين 1
حل المعادلة التربيعية التالية:
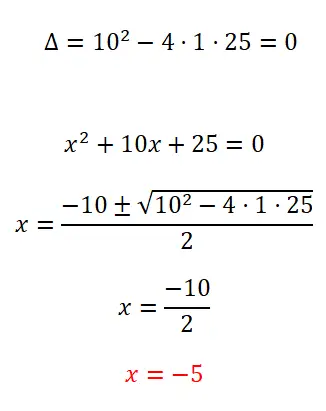
- نبدأ بحساب المميز لمعرفة عدد الحلول الممكنة.
- بما أن هذه معادلة تربيعية كاملة، فإننا نطبق الصيغة التربيعية ونحل العمليات الحسابية.
- نحصل على قيمة المجهول x.
تمرين 2
حل المعادلة التربيعية التالية:
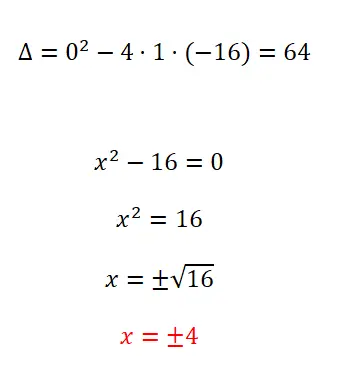
- نبدأ بحساب المميز.
- وبما أن لدينا معادلة تربيعية غير مكتملة حيث b = 0، فإننا نطبق المعيار على المعادلات من هذا النوع.
- نقوم بحل العملية الحسابية للحصول على النتيجة، ولا يمكننا أن ننسى علامة ±.
التمرين 3
حل المعادلة التربيعية غير المرتبة التالية:
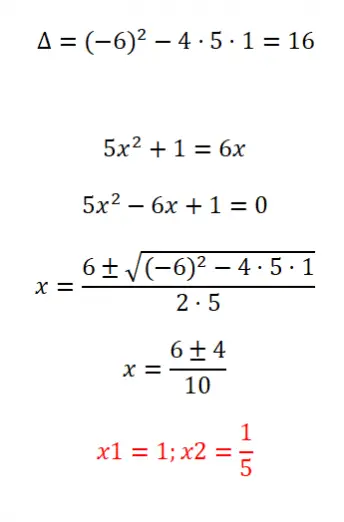
- نبدأ بحساب مميز المعادلة.
- قبل أن نتمكن من تطبيق الصيغة، نحتاج إلى ترتيب المعادلة وفقًا للبنية ax² + bx + c = 0.
- ثم نطبق الصيغة العامة.
- وأخيرا نحصل على النتائج.
التمرين 4
حل المعادلة التربيعية التالية عن طريق التحليل:
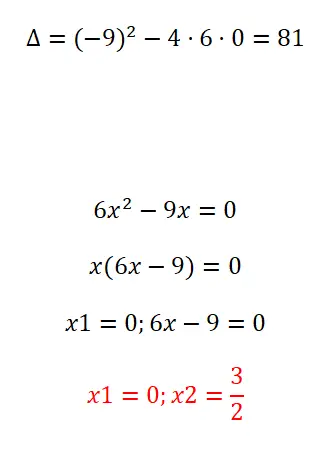
- نحسب المميز أولاً.
- بعد ذلك، نستخرج العامل المشترك لـ x.
- إذن الحل الأول هو x = 0.
- والثاني هو س = 3/2.
التمرين 5
حل المعادلة التربيعية الكاملة التي نوضحها أدناه:
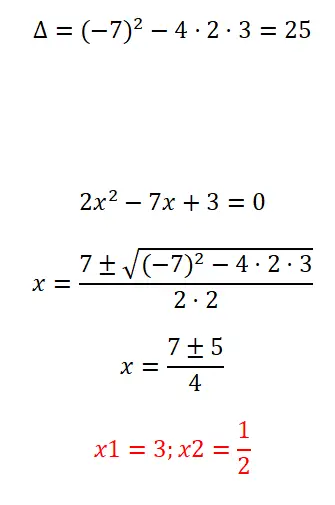
- كما هو الحال دائمًا، نحسب المميز لمعرفة عدد حلول المعادلة المعنية.
- بعد ذلك، نطبق الصيغة التربيعية، لأنها معادلة كاملة.
- وأخيرا، نعبر عن نتيجة المعادلة.
التمرين 6
حل المعادلة التربيعية بالكسور التي نقدمها:
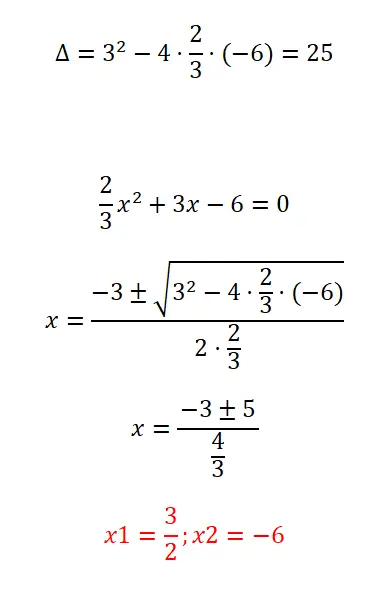
- نبدأ بحساب مميز التعبير.
- بعد ذلك، نطبق الصيغة التربيعية، مع الأخذ في الاعتبار أن المعامل “أ” يتكون من كسر.
- نحن نحل الحساب.
- ولدينا بالفعل جذري المعادلة.
التمرين 7
حل المعادلة التربيعية التالية:
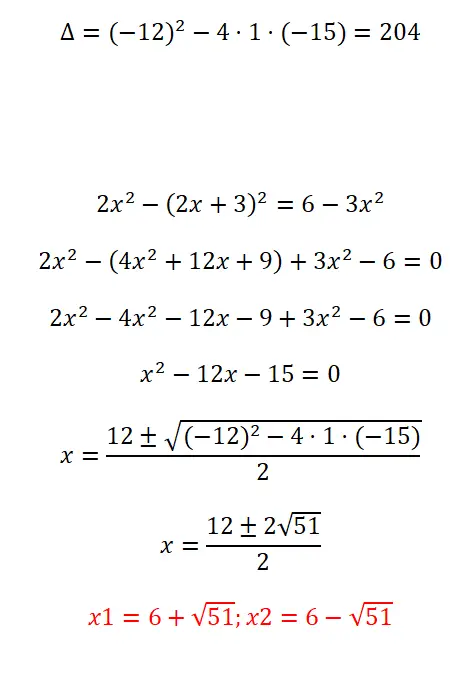
- نبدأ بحساب المميز.
- قبل تطبيق الصيغة، علينا تبسيط التعبير وإعطائه الصيغة ax² + b + c = 0.
- نعوض بجميع المعاملات في الصيغة ونحل العملية الحسابية.
- وأخيرا نحصل على النتيجة.
التمرين 8
إثبات حل المعادلة التربيعية التالية:
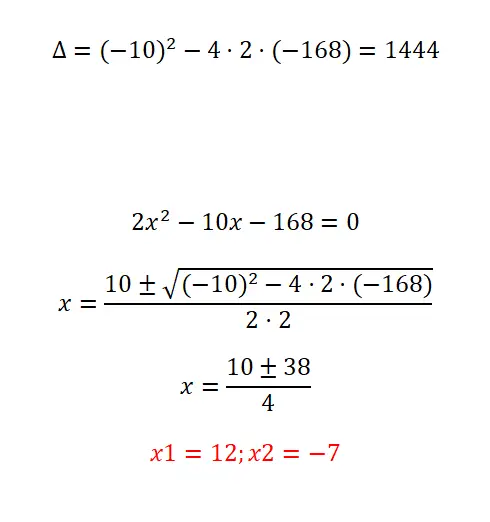
- نبدأ بحساب المميز.
- كما ترون، هذه معادلة تربيعية بسيطة، على الرغم من أن معاملاتها كبيرة جدًا. ولذلك، علينا أن نطبق الصيغة ونكون حذرين عند إجراء العمليات.
- في النهاية نحصل على كلا الحلين الممكنين.