المصفوفة المثلثية العلوية والسفلية

في هذه الصفحة ستشاهد ما هي المصفوفة المثلثية والأنواع المختلفة للمصفوفات المثلثية مع الأمثلة. بالإضافة إلى ذلك، ستجد كيفية حساب محدد المصفوفة المثلثية وما هي خصائص هذه المصفوفة المثيرة للاهتمام. وأخيرًا، سنوضح أيضًا ما هي مصفوفة هيسنبرج، لأنها مصفوفة مرتبطة بالمصفوفات المثلثية.

ما هي المصفوفة الثلاثية؟

تعريف المصفوفة الثلاثية:

المصفوفة المثلثية هي مصفوفة مربعة تكون فيها جميع العناصر الموجودة أعلى أو أسفل القطر الرئيسي صفر (0).

تستخدم المصفوفات المثلثية على نطاق واسع في حسابات الجبر الخطي، لأن قلب المصفوفة المثلثية أو حساب محددها أو حتى حل أنظمة المعادلات الخطية بهذا النوع من المصفوفات أسهل بكثير من المصفوفات التي تحتوي على عناصر أخرى غير 0 في جميع المواضع. .

المصفوفة الثلاثية العليا

المصفوفة المثلثية العليا هي مصفوفة مربعة تكون عناصرها الموجودة أسفل القطر الرئيسي صفر (0).

مثال على المصفوفة الثلاثية العليا:

مصفوفة مثلثية سفلية

المصفوفة المثلثية السفلية هي مصفوفة مربعة تحتوي على صفر (0) في كل عنصر يقع فوق القطر الرئيسي.

مثال على مصفوفة مثلثية سفلية:

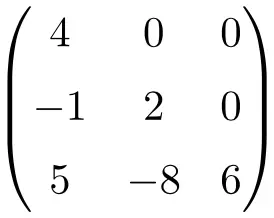
في بعض الأحيان تسمى هذه المصفوفات أيضًا بالحرف U للمصفوفة المثلثية العليا، وبالحرف L للمصفوفة المثلثية السفلية. على الرغم من أن هذه التسمية تستخدم بشكل أساسي في اللغة الإنجليزية، إلا أن حرف U يشير في الواقع إلى المصفوفة المثلثية العليا وحرف L إلى المصفوفة المثلثية السفلية .

أمثلة على المصفوفات الثلاثية

مصفوفة ثلاثية الأبعاد 2 × 2

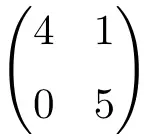
مصفوفة مثلثية من الرتبة 3×3

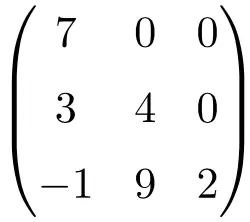
مصفوفة مثلثة مقاس 4×4

محدد المصفوفة الثلاثية

محدد المصفوفة المثلثية ، سواء كانت مثلثية علوية أو سفلية، هو حاصل ضرب العناصر الموجودة على القطر الرئيسي.

ألقِ نظرة على التمرين التالي الذي تم حله حول كيفية حساب ضرب عناصر القطر الرئيسي للمصفوفة المثلثية للعثور على محددها:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

يتم توضيح هذه النظرية بسهولة: ما عليك سوى حساب محدد المصفوفة المثلثية بواسطة الكتل (أو العوامل المساعدة). تم تفصيل هذا العرض التوضيحي أدناه باستخدام مصفوفة ثلاثية عامة:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

من ناحية أخرى، نحن نعلم أن المصفوفة تكون قابلة للعكس إذا كان محددها مختلفًا عن 0. لذلك، إذا لم يكن هناك أي عنصر على القطر الرئيسي يساوي 0، فإن المصفوفة المثلثية ستكون أيضًا قابلة للعكس، وبالتالي، ستكون منتظمة مصفوفة.

خصائص المصفوفة الثلاثية

الآن دعونا نرى ما هي خصائص المصفوفات المثلثية:

حاصل ضرب مصفوفتين مثلثيتين علويتين يساوي مصفوفة مثلثية علوية واحدة. والعكس صحيح: ضرب مصفوفتين مثلثيتين سفليتين يعطي مصفوفة مثلثية سفلية أخرى.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

تبديل المصفوفة المثلثية العلوية هو مصفوفة مثلثية سفلية، والعكس صحيح: تبديل المصفوفة المثلثية السفلية هو مصفوفة مثلثية عليا.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

تكون المصفوفة المثلثية قابلة للعكس إذا كانت جميع عناصرها على القطر الرئيسي غير صفرية، أي إذا كانت مختلفة عن الصفر. في مثل هذه الحالة، يكون معكوس المصفوفة المثلثية العلوية (السفلية) هو أيضًا مصفوفة مثلثية علوية (سفلية).

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

بالإضافة إلى ذلك، فإن القطر الرئيسي للمصفوفة المقلوبة سيحتوي دائمًا على معكوسات عناصر القطر الرئيسي للمصفوفة المثلثية الأصلية.

أي مصفوفة قطرية هي مصفوفة مثلثية عليا ومصفوفة مثلثية سفلية، على سبيل المثال:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

لذا فإن المصفوفة العددية هي أيضًا مصفوفة مثلثية علوية وسفلية. على سبيل المثال مصفوفة الهوية:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

من الواضح أن المصفوفة الصفرية هي أيضًا مصفوفة مثلثية علوية وسفلية، لأن العناصر الموجودة أعلى وأسفل القطر الرئيسي هي 0:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

القيم الذاتية (أو القيم الذاتية) للمصفوفة المثلثية هي عناصر القطر الرئيسي.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

المصفوفة المثلثية العلوية أو السفلية قادرة دائمًا على التخطيط القطري على أساس المتجهات الذاتية (أو المتجهات الذاتية).

يمكن تحليل أي مصفوفة إلى حاصل ضرب مصفوفة مثلثية سفلية ومصفوفة مثلثية عليا . أي أنه يمكن تحويل أي مصفوفة إلى ضرب مصفوفة ثلاثية. علاوة على ذلك، إذا كانت المصفوفة قابلة للعكس، فإن هذا التحويل يكون فريدًا. لتحليل المصفوفة إلى عوامل، غالبًا ما يتم استخدام طريقة تحليل LU.

تثليث المصفوفة

هناك العديد من النظريات حول المصفوفات التي يمكن تثليثها عن طريق تغيير القاعدة. ومع ذلك، سنرى هنا كيفية تثليث المصفوفة من خلال تطبيق التحويلات الأولية على الخطوط ، كما في طريقة غاوس.

على سبيل المثال:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

وبهذه الطريقة، نكون قد مثلثنا المصفوفة الأصلية بالفعل.

تذكر أن التحويلات الأولية المسموح بها بين السطور بالطريقة الغوسية هي:

استبدل سطرًا بالمجموعة الخطية من الخطوط الأخرى.
ضرب أو قسمة جميع الحدود في صف واحد على رقم غير 0.
تحرير خطوط الطلب.

مصفوفة هيسنبرج

تعريف مصفوفة هيسنبرج هو كما يلي:

مصفوفة هيسنبرج هي مصفوفة مثلثة “تقريبا” أي أن جميع عناصرها صفر بدءا من القطر الفرعي الأول (مصفوفة هيسنبرج العليا) أو القطر الفائق الأول (مصفوفة هيسنبرج السفلية).

أنا متأكد من أنه من الأفضل فهم ذلك باستخدام مثال مصفوفة هيسنبرج العليا ومثال آخر لمصفوفة هيسنبرج السفلية:

مصفوفة هيسنبرج العليا

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

مصفوفة هيسنبرج السفلى

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

المصفوفة التي تكون مصفوفة هيسنبرج العلوية والسفلية هي مصفوفة ثلاثية الأقطار .

سميت هذه المصفوفة على اسم كارل هيسنبرج، وهو مهندس وعالم رياضيات ألماني بارز في القرن العشرين.

وأخيرًا، يتميز هذا النوع من المصفوفات بخصوصية أنه إذا تم ضربه في مصفوفة مثلثة، فإن النتيجة تكون دائمًا مصفوفة هيسنبرج.

المصفوفة الثلاثية العلوية والسفلية