المسافة بين خطين في الفضاء (في R3)

ستجد في هذه الصفحة كيفية حساب المسافة بين خطين في الفضاء (في R3)، مهما كان نوعها (خطوط متوازية، قاطعة، متطابقة، قاطعة، متعامدة، إلخ). بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين التي تم حلها خطوة بخطوة.

كيفية حساب المسافة بين خطين

المسافة بين خطين هي أصغر مسافة بين أي نقطة على أحد الخطين وأي نقطة على الخط الآخر. هذه المسافة تقابل طول القطعة التي تنتقل من خط إلى آخر وتكون في نفس الوقت متعامدة مع كلا الخطين.

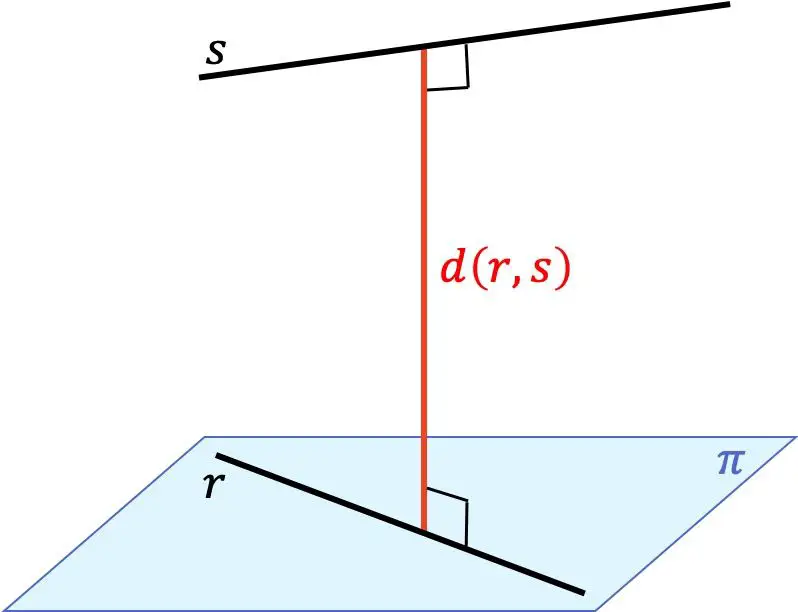
لذا فإن إيجاد المسافة بين خطين مختلفين في الفضاء ثلاثي الأبعاد يعتمد على الموضع النسبي بينهما:

إذا تطابق الخطان أو تقاطعا ، فإن المسافة بين الخطين تكون صفراً، لأنهما يتقاطعان (على الأقل) في نقطة واحدة.
عندما يكون الخطان متوازيين ، نحتاج إلى أخذ أي نقطة على أحد الخطين وحساب المسافة بين تلك النقطة والخط الآخر (أدناه لديك مثال لكيفية القيام بذلك).
إذا تقاطع الخطان في الفضاء، نحتاج إلى تطبيق صيغة المسافة بين خطين متقاطعين (انظر أدناه للحصول على شرح مفصل).

لذا، لحساب المسافة بين خطين، يجب عليك أولاً معرفة نوع الخطوط ثم، حسب الحالة، استخدم صيغة أو أخرى. لذلك، من المهم أن تتقن بالفعل كيفية العثور على الموضع النسبي لخطين في الفضاء قبل المتابعة، ولكن إذا كنت لا تتذكر كيف تم ذلك في الرابط سترى شرحًا كاملاً للغاية بالإضافة إلى أمثلة وتمارين تم حلها خطوة بخطوة.

كيفية العثور على المسافة بين خطين متوازيين في الفضاء

يتم حساب المسافة بين خطين متوازيين في الفضاء (في R3) بنفس الطريقة كما في المستوى (في R2): عليك أن تأخذ نقطة على أي من الخطين وتجد مسافة هذه النقطة على الآخر خط.

وبالتالي، فإن صيغة حساب المسافة من نقطة إلى خط في ثلاثة أبعاد (والتي تستخدم لتحديد المسافة بين خطين متوازيين) هي:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

ذهب:

$\lvert \vv{\text{v}}_r \rvert$

هو حجم متجه الاتجاه للخط

$r.$
$Q$

هي نقطة على السطر

$r,$

$P$

نقطة على السطر

$s$

و

$\vv{QP}$

المتجه المحدد بالنقطتين
$\lvert \vv{QP} \times \vv{\text{v}}_r \rvert$

هو حجم المنتج المتقاطع بين المتجهات

$\vv{QP}$

و

$\vv{\text{v}}_r$

على سبيل المثال، سنقوم بحل مسألة المسافة بين خطين متوازيين في الفضاء:

ما المسافة بين الخطين المتوازيين التاليين؟

$r: \ (x,y,z) = (2,1,1) + t(-1,3,2)$

$s: \ (x,y,z) = (-2,4,1) + t(2,-6,-4)$

يتم التعبير عن كلا الخطين في شكل معادلة متجهة، لذلك يمكننا بسهولة معرفة متجه الاتجاه ونقطة كل منهما:

$\displaystyle r : \ \begin{cases}\vv{\text{v}}_r=(-1,3,2) \\[1.7ex] Q(2,1,1) \end{cases} \qquad \qquad s: \ \begin{cases}\vv{\text{v}}_s=(2,-6,-4) \\[1.7ex] P(-2,4,1) \end{cases}$

إذا كانت لديك أي شكوك حول كيفية تحديد متجه الاتجاه ونقطة الخط، ننصحك بإلقاء نظرة على شرح معادلة الخط . لقد شرحنا ذلك لجميع معادلات الخط، لأن العثور على متجه الاتجاه والنقطة التي تنتمي إلى الخط يعتمد على نوع المعادلة التي يتم التعبير فيها عن الخط.

الآن، لإيجاد المسافة بين الخطين المتوازيين، علينا تطبيق صيغة المسافة من نقطة إلى خط مستقيم:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}$

ومن ناحية أخرى، نحسب وحدة المتجه الناتجة عن حاصل ضرب المتجه. إذا كانت لديك شكوك حول كيفية حسابها، يمكنك الرجوع إلى صيغة المنتج المتجه ، حيث، بالإضافة إلى ذلك، ستتمكن من رؤية الأمثلة والتمارين التي تم حلها لهذه العملية بين المتجهات.

$\vv{QP} = Q - P = (2,1,1)-(-2,4,1) = (4,-3,0)$

$\vv{QP} \times \vv{\text{v}}_r =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 4&-3&0 \\[1.1ex] -1&3&2 \end{vmatrix}=-6\vv{i} -8\vv{j}+9\vv{k}$

$\left|\vv{QP} \times \vv{\text{v}}_r \right| =\sqrt{(-6)^2+(-8)^2+9^2} = \sqrt{36+64+81} = \sqrt{181}$

ومن ناحية أخرى، نجد مقدار متجه الخط المستقيم

$r:$

$\lvert \vv{\text{v}}_r \rvert = \sqrt{(-1)^2+3^2+2^2} = \sqrt{1+9+4} = \sqrt{14}$

أخيرًا، نعوض بقيمة كل حد في الصيغة ونحسب المسافة بين السطور:

$d(s,r)=d(P,r)=\cfrac{\lvert \vv{QP} \times \vv{\text{v}}_r \rvert}{\lvert \vv{\text{v}}_r \rvert}=\cfrac{\sqrt{181}}{\sqrt{14}} = \bm{3,60}$

ومن ثم، فإن المسافة بين الخطين هي 3.60 وحدة.

كيفية تحديد المسافة بين خطين متقاطعين في الفضاء

كما رأينا في البداية، فإن طريقة تحديد المسافة بين خطين متقاطعين تختلف عن طريقة تحديد المسافات بين الخطوط المتوازية.

وبالتالي، هناك عدة طرق لتحديد المسافة بين خطين متقاطعين في الفضاء. في هذه الصفحة سنشرح إجراء واحد فقط، وهو الأبسط، لأن الطريقتين الأخريين أطول وأكثر تعقيدًا، في الواقع، لا يتم استخدامهما عمليًا.

ليكن متجه الاتجاه وأي نقطة من خطين متقاطعين:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} \\[2ex] A\end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}} \\[2ex] B\end{cases}$

صيغة المسافة بين خطين متقاطعين هي:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

ذهب

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|$

هي القيمة المطلقة للمنتج المختلط للمتجهات

$\vv{\text{u}}, \vv{\text{v}}$

والمتجه المحدد بالنقاط

$A$

$B$

. ومن ناحية أخرى،

$\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert$

هي سعة حاصل الضرب المتقاطع بين متجهات الاتجاه للخطين المتقاطعين.

ولكي تتمكن من معرفة كيفية تحديد المسافة بين خطين متقاطعين، سنحل مسألة كمثال:

ما المسافة بين الخطين المتقاطعين التاليين؟

$r: \ \cfrac{x-1}{2} = \cfrac{y-2}{4} = \cfrac{z+2}{-1}$

$s: \ \cfrac{x-3}{1} = \cfrac{y+1}{3} = \cfrac{z-1}{-2}$

أولًا، علينا تحديد متجه الاتجاه ونقطة على كل خط. ويتم التعبير عن الخطين في شكل معادلة مستمرة، وبالتالي:

$\displaystyle r: \ \begin{cases} \vv{\text{u}} =(2,4,-1) \\[2ex] A(1,2,-2) \end{cases} \qquad \qquad s: \ \begin{cases} \vv{\text{v}}=(1,3,-2) \\[2ex] B(3,-1,1)\end{cases}$

والآن نطبق صيغة المسافة بين خطين متقاطعين:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert}$

من ناحية نحل المنتج المختلط (أو المنتج العددي الثلاثي):

$\vv{AB} = B - A = (3,-1,1) - (1,2,-2) = (2,-3,3)$

$\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right| =\left| \begin{vmatrix} 2&4&-1 \\[1.1ex] 1&3&-2 \\[1.1ex] 2&-3&3 \end{vmatrix}\right| = \left| -13 \right| =13$

ومن ناحية أخرى، نجد وحدة الضرب الاتجاهي (أو المنتج الاتجاهي):

$\vv{\text{u}} \times \vv{\text{v}} =\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 2&4&-1 \\[1.1ex] 1&3&-2 \end{vmatrix}=-5\vv{i} +3\vv{j}+2\vv{k}$

$\left| \vv{\text{u}} \times \vv{\text{v}} \right| =\sqrt{5^2+3^2+2^2} = \sqrt{25+9+4} = \sqrt{38}$

أخيرًا، نعوض بقيمة كل حد في صيغة المسافة بين خطين متقاطعين:

$d(r,s)=\cfrac{\left|\left[\vv{\text{u}},\vv{\text{v}},\vv{AB}\right]\right|}{\lvert \vv{\text{u}} \times \vv{\text{v}} \rvert} = \cfrac{13}{\sqrt{38}}= \bm{2,11}$

المسافة بين خطين في الفضاء (في r3)

كيفية حساب المسافة بين خطين

كيفية العثور على المسافة بين خطين متوازيين في الفضاء

كيفية تحديد المسافة بين خطين متقاطعين في الفضاء

اترك تعليقاً إلغاء الرد