Magic Squares هي لعبة ألغاز رياضية تدرب مهاراتنا الحسابية بطريقة ممتعة ومثيرة. ولهذا السبب فهو أحد أفضل الموارد لتدريس الرياضيات للطلاب الصغار.
ما هي المصفوفة السحرية وكيف يتم حلها؟
المربع السحري هو نوع من الجدول أو المصفوفة المكونة من صناديق مختلفة، تُكتب فيها الأعداد الصحيحة . لكن لا يمكن تركيبها تحت أي ظرف من الظروف؛ يجب احترام مجموعة من القواعد:
- جميع المجاميع السحرية (مجموعات جميع قيم أي خط أفقي أو رأسي أو قطري) يجب أن تعطي دائمًا قيمة مكافئة للثابت السحري (وهي قيمة واحدة).
- لا يمكن تكرار أي رقم مرتين.
- يمكنك فقط استخدام الأرقام المتتالية (على سبيل المثال، من 1 إلى 9) أو الأرقام التي تتبع سلسلة معينة، على سبيل المثال: الأرقام الفردية ومضاعفات الرقم 5 وغيرها.
ومن المهم أيضًا التأكيد على أنه يمكننا إجراء تصنيفات مختلفة للمربعات اعتمادًا على بنيتها. الأول حسب درجة المربع وهو ما يعادل عدد الخلايا الموجودة في الصف أو العمود. والثاني حسب نوع درجة الجدول ( أرقام زوجية أو أرقام فردية). ومن خلال هذه الفروق يمكننا تنظيم جميع المربعات في فئات مختلفة، على الرغم من أننا سنفصل ذلك لاحقًا.
كيفية حل المربعات السحرية؟
لحل لعبة الرياضيات هذه، يمكننا استخدام طريقتين مختلفتين: استخدام الهندسة أو حساب الثابت السحري. كلا الإجراءين صالحان بنفس القدر، على الرغم من أن أحدهما يسمح لك بتحقيق النتيجة بسرعة أكبر، بينما يتطلب الآخر مزيدًا من الوقت والتفكير . بعد ذلك، سنشرح كلتا الطريقتين، حتى تتمكن من اختيار الطريقة التي تفضلها ويمكنك التكيف بشكل أفضل مع كل موقف.
ما هي صيغة المربعات السحرية؟
الطريقة الأولى تتمثل في حساب الثابت السحري ، والذي يجب علينا استخدام الصيغة التالية له: n(n 2 +1)/2، حيث n هي درجة المربع. وبمجرد حصولنا على هذه القيمة، كل ما يتبقى هو تجربة مجموعات مختلفة من الأرقام، والتي تسمح لنا بمساواة المجموع السحري للمربع بأكمله مع الثابت. بمعنى آخر، نحن بحاجة إلى تكوين مجموعات من الأرقام التي تضيف ما يصل إلى قيمة الثابت، بحيث تكون الصورة بأكملها متوازنة.
كيفية حل المربعات السحرية باستخدام الهندسة؟
ثانيًا، يمكننا حل المربعات السحرية باستخدام الهندسة . على الرغم من أنه تجدر الإشارة إلى أن هذه الطريقة بسيطة جدًا ولا تتطلب منك ممارسة مهاراتك الحسابية، فهي منهجية بحتة. ومع ذلك، سنشرح الإجراء الخاص بحل المربعات ذات الرتبة الزوجية والمربعات ذات الرتبة الفردية.
كيفية حل المربعات السحرية بأرقام فردية؟
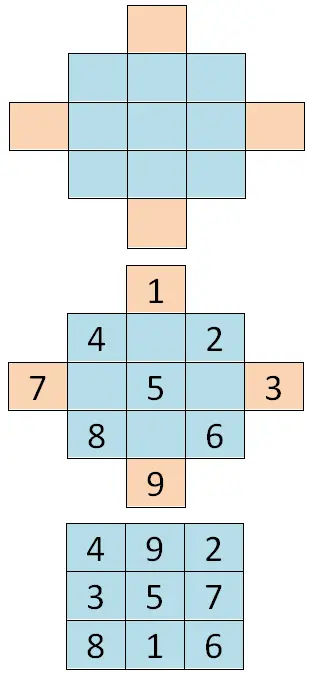
لحل هذه الحالة الأولى، يجب عليك إضافة خلايا إلى الجدول الأولي حتى تحصل على نوع من المعين. ثم علينا أن نكتب جميع الأرقام المتتالية بدءًا من الرقم الأول من السلسلة (في حالتنا 1) وسنتبع أقطار الماسة . وأخيرا، نحن بحاجة إلى “مضاعفة” الرقم، وبالتالي فإن قيم الخلايا الخارجية تذهب إلى الجانب الآخر. إذن تتقاطع الخلايا الخارجية للمحور العمودي، ثم يحدث نفس الشيء مع خلايا المحور الأفقي، أدناه يمكنك رؤية مثال:
كيفية حل المربعات السحرية ذات الترتيب الزوجي؟
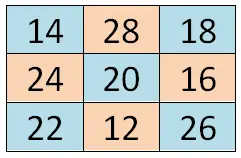
لحل المربع السحري ذي الترتيب الزوجي (المربعات السحرية التي تحتوي على عدد زوجي من الصفوف والأعمدة)، يمكننا اللجوء إلى طريقة مختلفة بعض الشيء عن الطريقة السابقة، ولكنها تعتمد أيضًا على الهندسة. سنبدأ بكتابة الرقم الأول من السلسلة (في حالتنا 1) في الزاوية اليسرى العليا. بعد ذلك، سوف نجتاز القطرين الرئيسيين ونكتب القيم المقابلة لموضع كل مربع.
بمجرد أن نكتب القطرين الرئيسيين، سيتعين علينا أن نضع أنفسنا في المربع الفارغ الأول بدءًا من الزاوية اليمنى السفلية (المربع 15 في حالتنا). هناك سنكتب القيمة الثانية من السلسلة وسنكتب القيم المتبقية بالترتيب (من الأصغر إلى الأكبر)، مع استكمال الخلايا من اليمين إلى اليسار ومن الأسفل إلى الأعلى . ولتوضيح الأمر أكثر، يمكنك التوجه بالصورة التي نعرضها لك أدناه:
كيفية بناء المربعات السحرية؟
لبناء المربعات السحرية بأنفسنا، يمكننا اتباع عدة إجراءات، من بينها سنسلط الضوء على اثنين منها. تجدر الإشارة إلى أنه سيتم استخدام كل منها لإنشاء مربعات من أنواع مختلفة، لذلك سيتعين عليك اختيار الطريقة بعناية اعتمادًا على المربع الذي تريد إنشاءه:
الطريقة السيامية
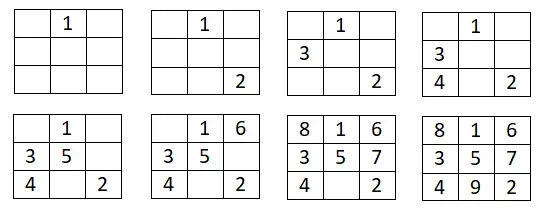
هذه الطريقة الأولى بسيطة للغاية وتساعدنا بشكل خاص في بناء مربعات سحرية غريبة بأي حجم. الإجراء الذي يجب اتباعه بسيط جدًا، حيث سنكتب الرقم الأول من السلسلة في المربع المركزي للصف الأول. ومن هناك سنعود بالترتيب في المتتابعة الحسابية التي اخترناها، ونكتب الرقم التالي للأعلى ولليمين . ومع ذلك، إذا كان هذا الموضع خارج المربع المرسوم، فسيتعين علينا الانتقال إلى الصف أو العمود الأخير. وإذا انتهى بنا الأمر إلى مربع كامل، فسيتعين علينا النزول بمقدار مربع واحد من آخر مربع رقم أدخلناه ثم سنستمر بنفس الطريقة.
أدناه يمكنك رؤية مثال 3×3:
طريقة ستراشي للمربعات السحرية
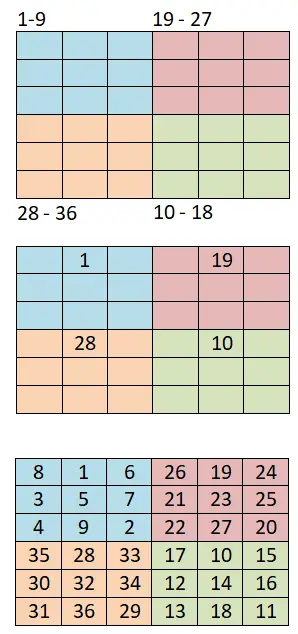
لإنشاء مربعات سحرية من الترتيب 4k + 2 أزواج ، سنستخدم هذه الطريقة الأخرى، والتي تعتمد على الطريقة السابقة (الطريقة السيامية) وهي أيضًا بسيطة جدًا. يمكنك أدناه الاطلاع على الخطوات التي يجب اتباعها ومثال عملي للمربع السحري مقاس 6 × 6:
- التقسيم إلى أرباع أصغر: أول شيء يتعين علينا القيام به هو تقسيم اللوحة إلى مربعات أصغر، على سبيل المثال، إذا كان لدينا لوحة مقاس 6×6، فسنحتاج إلى إنشاء أربعة أرباع متساوية من مربعات 3×3.
- استخدم الطريقة السيامية: ثم سنخصص نطاقًا من الأرقام لكل ربع صغير، على سبيل المثال إذا بدأنا التسلسل بـ 1، ستكون النطاقات: 1-9 (الأول)، 10-18 (الرابع)، 19-27 (الثاني) و28-36 (الثالث).
طريقة كونواي LUX للمربعات السحرية
سوف نستخدم النظام الأخير عندما نريد إنشاء مربعات سحرية من الرتبة 4n + 2 حيث n عدد طبيعي. لذا فإن الإجراء الذي سنتبعه لإنشاء مربعات بهذا النمط هو كما يلي:
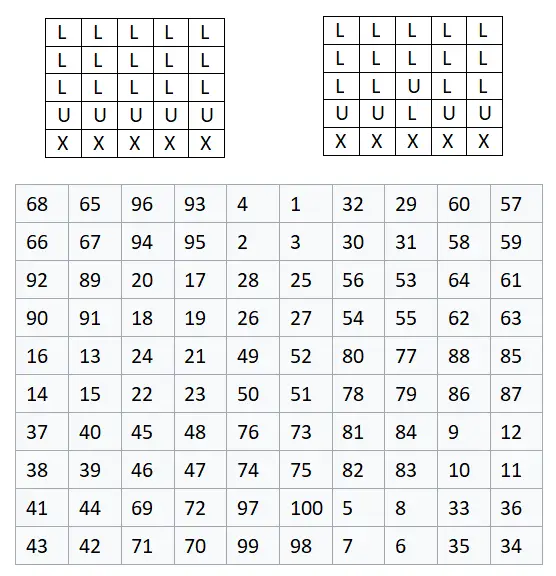
- إنشاء الجدول أو المصفوفة: سنبدأ بإنشاء مصفوفة من الدرجة 2n + 1، حيث n عدد طبيعي. وبهذا سنتمكن من تصميم الجدول وسنضع في اعتبارنا درجته ثم نبدأ بالتصميم.
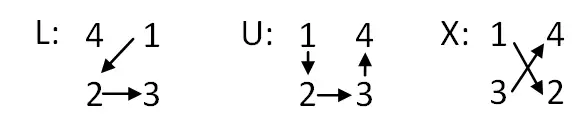
- تحديد موضع الحروف: بمجرد إنشاء الجدول، سيتعين عليك الكتابة من أعلى إلى أسفل: n + 1 سطر من L، وسطر واحد من U، وn – 1 سطر من X. وبعد ذلك، سيتعين عليك استبدال U في المنتصف مع حرف L في الأعلى.
- مبادلة الحروف بالقيم العددية: الآن سنحتاج إلى استبدال الحروف بمجموعات من أربعة أرقام متتالية. اعتمادا على الرسالة، سنقدم أمرا أو آخر للأرقام. موضح أدناه:
سنبدأ ببناء مصفوفة 5×5 ، إذًا n = 2، نظرًا لأن: 2n + 1 = 2 · 2 + 1 = 5. وهذا يعني أن حجم المصفوفة سينتهي بـ 10×10، لأنه كما نحن سبق أن قلنا أن كل خلية تحتوي على حرف تعادل مجموعة من أربعة أرقام، أي مصفوفة 2×2. أدناه يمكنك مشاهدة المثال النهائي الذي قمنا فيه باستبدال كل حرف بمجموعة من أربعة أرقام بالترتيب الموضح في الصورة:
تمارين المربعات السحرية
بعد ذلك، نقدم لك بعض المربعات السحرية غير المكتملة وسيتعين عليك ملئها بنفسك، وذلك بفضل المفاهيم التي شرحناها في هذه المقالة. تذكر أنه يمكنك استخدام أي من الأساليب التي يتم تدريسها. بالإضافة إلى ذلك، عليك أن تأخذ في الاعتبار أن 1 قد لا يكون الرقم الأول في السلسلة، على الرغم من أنه سيضعه في الإعلان. وعند الانتهاء من أحد التمارين، ستتمكن من رؤية الحل أسفل العبارة.
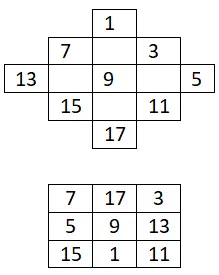
المربع السحري 3×3
قم ببناء مربع سحري 3×3 بأرقام فردية فقط:
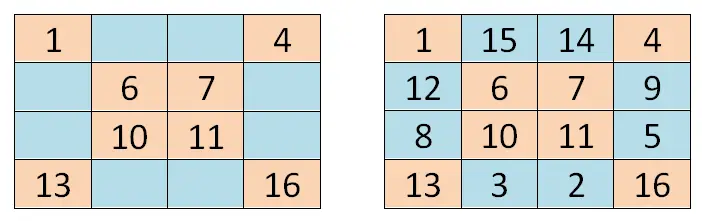
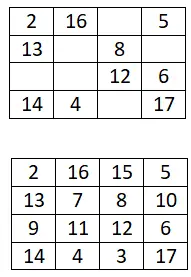
المربع السحري 4×4
أكمل المربع السحري 4×4 التالي:
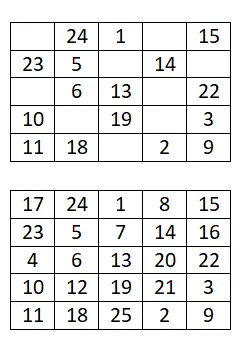
المربع السحري 5×5
أكمل المربع السحري التالي 5×5:
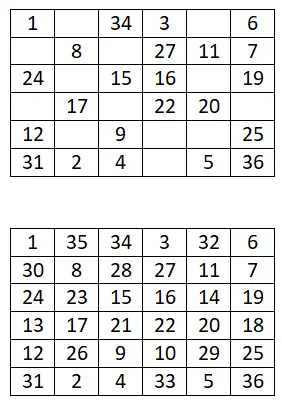
المربع السحري 6×6
أكمل المربع السحري التالي 6×6: