الانحدار الخطي هو أسلوب إحصائي يستخدم لدراسة العلاقة بين متغيرين مستمرين . الفكرة الرئيسية للانحدار الخطي هي العثور على الخط المستقيم الذي يناسب البيانات بشكل أفضل. بالإضافة إلى ذلك، فهو يسمح لك بالتنبؤ بقيمة متغير واحد بناءً على قيمة متغير آخر.
يسمى هذا الخط المستقيم “الانحدار” ويستخدم للتنبؤ بقيم غير معروفة أو لفهم العلاقة بين المتغيرات. باختصار، الانحدار الخطي هو أداة لتحليل ونمذجة العلاقة بين متغيرين مستمرين.
لماذا يعتبر الانحدار الخطي مهم؟
يعد الانحدار الخطي مهمًا لأنه يسمح لك بنمذجة وتحليل العلاقة بين متغيرين مستمرين ، مما قد يكون مفيدًا للتنبؤ بالقيم المستقبلية وتحديد الأنماط والاتجاهات في البيانات.
بالإضافة إلى ذلك، يعد الانحدار الخطي أداة أساسية في الإحصاء ومعظم مجالات البحث العلمي والاجتماعي، بما في ذلك الاقتصاد وعلم النفس والطب والهندسة والفيزياء وغيرها. كما أنها تستخدم في اتخاذ القرارات التجارية وتحسين العمليات في الصناعة والأعمال.
باختصار، يعد الانحدار الخطي أداة قوية ومتعددة الاستخدامات تتيح التحليل والفهم الأفضل للبيانات والعلاقات بين المتغيرات في مختلف مجالات البحث والممارسة.
ما هي أنواع الانحدار الخطي؟
هناك عدة أنواع من الانحدار الخطي، بعض منها:
الانحدار الخطي البسيط
تحليل الانحدار الخطي البسيط هو أداة تستخدم على نطاق واسع لدراسة تأثير متغير مستقل على متغير تابع واحد ، حيث يعتبر أن هناك علاقة خطية بينهما. تتيح لنا معادلة الانحدار الخطي البسيطة تقدير قيم المتغير التابع بناءً على قيم المتغير المستقل.
صيغة الانحدار الخطي البسيطة هي:
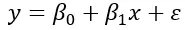
حيث β 0 هي قيمة المتغير التابع عندما يكون المتغير المستقل صفراً. يمثل β 1 التغير في المتغير التابع لكل وحدة تغير في المتغير المستقل ويمثل ε المتبقي أو الخطأ. أي تباين البيانات الذي لا يمكن تفسيره بالعلاقة الخطية للصيغة.
الانحدار الخطي المتعدد
يتم استخدام الانحدار الخطي المتعدد عندما يكون هناك أكثر من متغير مستقل يمكن أن يؤثر على المتغير التابع قيد الدراسة.
صيغة الانحدار الخطي المتعدد هي:
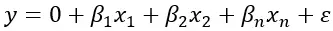
حيث تمثل Y المتغير التابع ، β 1 ، β 2 ، β n هي المتغيرات المستقلة التي يمكن أن تؤثر على قيمة Y، والانحدار و ε يمثل الخطأ الموجود المحتمل. تتيح لنا هذه الصيغة تقدير قيمة Y بناءً على قيم المتغيرات المستقلة.
ما هي صيغة الانحدار الخطي؟
صيغة الانحدار الخطي هي:
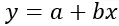
ذهب:
y هو المتغير التابع (أو الاستجابة) الذي سيتم التنبؤ به
x هو المتغير المستقل (أو المتنبئ) المستخدم في التنبؤ
a هو التقاطع (أو النقطة التي يتقاطع فيها خط الانحدار مع المحور Y عندما يكون x = 0)
b هو ميل خط الانحدار (يشير إلى معدل تغير y لكل تغيير في x)
للعثور على قيمتي a وb، نستخدم طريقة المربعات الصغرى التي تسعى إلى تقليل مجموع الأخطاء المربعة بين القيم المرصودة والقيم المتوقعة بواسطة خط الانحدار.
وهنا الصيغ:
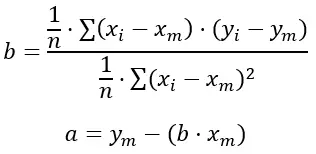
ذهب:
n هو العدد الإجمالي لمجموعات البيانات لدينا.
x i و y i هما القيمتان اللتان نأخذهما في الجمع.
x m و y m هما متوسط قيم كل متغير.
كيفية تطبيق طريقة الانحدار الخطي؟
يمكن تطبيق طريقة الانحدار الخطي باتباع الخطوات التالية:
- جمع البيانات : أول ما عليك فعله هو جمع البيانات التي تهمك. على سبيل المثال، إذا كنت تريد دراسة العلاقة بين الراتب وعمر مجموعة من الأشخاص، فأنت بحاجة إلى جمع معلومات عن الراتب وعمر كل منهم.
- رسم البيانات – بعد ذلك، تحتاج إلى رسم البيانات على المستوى الديكارتي، حيث يتم وضع المتغير المستقل (في هذه الحالة، العمر) على المحور الأفقي ويتم وضع المتغير التابع (الراتب) على المحور الرأسي.
- تحديد خط الانحدار : يجب تحديد خط الانحدار الذي يناسب البيانات بشكل أفضل. يتم الحصول على هذا الخط من صيغة الانحدار الخطي، والتي يتم حسابها باستخدام البيانات الإحصائية النموذجية .
- تقييم مدى ملاءمة – من المهم تقييم مدى ملاءمة خط الانحدار للبيانات. ويمكن القيام بذلك باستخدام القياسات الإحصائية.
- إجراء تنبؤات – أخيرًا، يمكن إجراء التنبؤات باستخدام خط الانحدار الناتج. على سبيل المثال، إذا كنت تريد التنبؤ براتب شخص يبلغ من العمر 30 عامًا، فيمكنك استخدام صيغة الانحدار الخطي واستبدال قيمة العمر بها.
ومن المهم ملاحظة أن هذه الخطوات قد تختلف قليلاً حسب نوع الانحدار الخطي المستخدم والبرنامج الإحصائي المستخدم.
ما هو الانحدار الخطي المستخدم؟
يتم استخدام الانحدار الخطي عندما تريد تحليل العلاقة بين متغيرين ، حيث يمكن لمتغير واحد أن يؤثر على قيمة متغير آخر. لذلك، يمكن استخدام الانحدار الخطي لفهم كيفية تأثير المتغير المستقل على المتغير التابع والتنبؤ بقيمة المتغير التابع بناءً على المتغير المستقل.
ومن المهم ملاحظة أن الانحدار الخطي يفترض أن العلاقة بين المتغيرين خطية ، أي أن التغير في المتغير التابع يتناسب مع التغير في المتغير المستقل.
لذلك، يجب استخدام الانحدار الخطي عند الاشتباه في وجود علاقة خطية بين المتغيرين. إذا لم يتم استيفاء هذا الشرط، فقد يكون من الأفضل استخدام نماذج الانحدار غير الخطية الأخرى أو الأساليب الإحصائية المختلفة.
ما هي تطبيقات الانحدار الخطي؟
يستخدم الانحدار الخطي في مجموعة واسعة من التطبيقات في مجالات مثل الإحصاء والاقتصاد والهندسة والعلوم الاجتماعية وعلم الأحياء وغيرها. فيما يلي بعض التطبيقات الأكثر شيوعًا للانحدار الخطي:
- تحليل الاتجاه – لتحليل الاتجاهات في البيانات التاريخية والتنبؤ بالاتجاهات المستقبلية.
- التنبؤ – التنبؤ بالقيمة المستقبلية لمتغير بناءً على القيم السابقة لمتغير واحد أو أكثر.
- أبحاث السوق : دراسة العلاقة بين الطلب على المنتج وسعره.
- التحليل المالي – دراسة العلاقة بين إيرادات الشركة ونفقاتها والتنبؤ بالنتائج المالية المستقبلية.
- الدراسات الوبائية : دراسة العلاقة بين التعرض لأحد عوامل الخطر واحتمالية الإصابة بالمرض.
- العلوم الاجتماعية – دراسة العلاقة بين متغيرين أو أكثر في مجالات مثل علم النفس وعلم الاجتماع والعلوم السياسية.
- بحوث العمليات – يستخدم الانحدار الخطي لنمذجة وتحسين الأنظمة المعقدة في مجالات مثل الهندسة الصناعية والخدمات اللوجستية.
- العلوم البيئية – تستخدم لدراسة العلاقة بين العوامل البيئية وتأثيراتها على النظم البيئية.
ما هي البقايا في الانحدار الخطي؟
البقايا في الانحدار الخطي هي الفرق بين القيم المرصودة للمتغير التابع والقيم التي تنبأ بها نموذج الانحدار الخطي . بمعنى آخر، هي المسافة العمودية بين نقاط البيانات الفعلية وخط الانحدار.
الفكرة وراء البقايا هي أنه إذا كان خط الانحدار يناسب البيانات بشكل جيد، فيجب أن تكون البقايا صغيرة وعشوائية. إذا كانت البقايا كبيرة أو تتبع نمطًا معينًا، فقد يكون ذلك علامة على أن العلاقة بين المتغيرات ليست خطية أو أن نموذج الانحدار الخطي غير مناسب للبيانات.
تُستخدم البقايا أيضًا لتقييم دقة نموذج الانحدار الخطي وتحديد القيم المتطرفة أو نقاط البيانات المؤثرة التي قد تؤثر على جودة النموذج.
هل يمكنني تشغيل الانحدار الخطي مع أكثر من متغير تابع؟
في الانحدار الخطي، يكون المتغير التابع دائمًا متغيرًا واحدًا. ومع ذلك، يمكن أن يكون لديك أكثر من متغير مستقل. في هذه الحالة، سنتحدث عن الانحدار الخطي المتعدد .
في الانحدار الخطي المتعدد، الهدف هو دراسة تأثير المتغيرات المستقلة المتعددة على متغير تابع واحد.
كيف يمكنني تفسير المعاملات في الانحدار الخطي؟
في الانحدار الخطي، تمثل المعاملات ميل وتقاطع خط الانحدار . ويشير الميل إلى التغير في المتغير التابع لكل وحدة تغير في المتغير المستقل، بينما يمثل التقاطع قيمة المتغير التابع عندما يكون المتغير المستقل مساوياً للصفر.
أمثلة عددية للانحدار الخطي
مثال بسيط قد يكون ما يلي:
لنفترض أن لدينا بيانات العمر والطول التالية لمجموعة من الأشخاص:
| سنوات من العمر) | الطول (سم) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| أربعة خمسة | 190 |
نريد تحديد ما إذا كانت هناك علاقة بين عمر هؤلاء الأشخاص وطولهم. للقيام بذلك، سوف نستخدم الانحدار الخطي.
أولاً، يمكننا رسم رسم بياني إحصائي باستخدام البيانات (في هذه الحالة نوصي باستخدام مخطط التشتت):
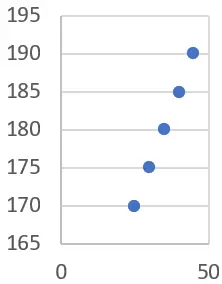
يمكننا أن نرى أن هناك اتجاهًا واضحًا وهو أنه مع زيادة العمر، يزداد الطول أيضًا. يمكننا تأكيد ذلك عن طريق حساب خط الانحدار الخطي.
وبحساب معاملات خط الانحدار الخطي بالصيغ التي رأيناها سابقاً نحصل على:
عند = 145
ب = 1
وبالتالي فإن معادلة خط الانحدار الخطي هي:
الطول = 145 + 1 العمر
يمكننا استخدام هذه المعادلة للتنبؤ بطول الشخص بناءً على عمره. على سبيل المثال، إذا كان عمر الشخص 32 عامًا، فيمكننا التنبؤ بأن طوله سيكون:
الارتفاع = 145 + 1 32 = 177 سم