إضافة ناقلات

تشرح هذه الصفحة كيفية إضافة متجهين في المستوى، بيانياً وعددياً. هناك ثلاث طرق لإضافتها بيانيًا: طريقة متوازي الأضلاع، وطريقة الرأس إلى الذيل، وطريقة المضلع. بالإضافة إلى ذلك، ستجد أيضًا تمارين محلولة حول إضافة المتجهات وجميع خصائص إضافة المتجهات.

كيفية إضافة ناقلين بيانيا؟

في الأساس هناك طريقتان لإضافة المتجهات من تمثيل الرسم البياني الخاص بها. مع كلا الشكلين يتم الحصول على نفس النتيجة، لكن البعض يفضل إضافتهم باستخدام طريقة الرأس والذيل والبعض الآخر باستخدام طريقة متوازي الأضلاع . ولذلك سنشرح لك الطريقتين حتى تختار الطريقة التي تفضلها. 😉

ومن ناحية أخرى، يتم استخدام هاتين الطريقتين لإضافة متجهين، لكن ماذا يحدث إذا أردنا إضافة أكثر من متجهين؟ ولذلك فمن الضروري استخدام طريقة المضلع ، والتي تتمثل في استخدام طريقة متوازي الأضلاع بالتتابع. ستجد أيضًا شرحًا لها بعد طريقتي الرأس والذيل ومتوازي الأضلاع.

طريقة أو قاعدة متوازي الأضلاع

قاعدة متوازي الأضلاع أو طريقة متوازي الأضلاع (أو قانون متوازي الأضلاع) هي إجراء رسومي يسمح لك بإيجاد مجموع متجهين بطريقة بسيطة للغاية. الخطوات التي يجب اتباعها لتطبيق هذه العملية هي كما يلي:

أولًا، نرسم المتجهات ونضعها في نفس نقطة التطبيق، أي أننا نضع أصول كلا المتجهين في نفس النقطة.
ثم نرسم في نهاية أحد المتجهين خطًا موازيًا للمتجه الآخر. ونكرر الخطوة مع المتجه الآخر. وبالتالي سوف نحصل على رسم متوازي الأضلاع (ومن هنا جاء اسم القاعدة).
وأخيرًا، ستكون نتيجة المجموع هي المتجه الذي ينتقل من الأصل المشترك إلى النقطة التي يتقاطع فيها الخطان المتوازيان.

انظر إلى المثال العام التالي الذي يتم فيه إضافة متجهين باستخدام قاعدة متوازي الأضلاع:

كيفية إضافة متجهين باستخدام قاعدة متوازي الأضلاع

نتيجة مجموع المتجهات هو قطر متوازي الأضلاع الذي تشكله مع متوازياتها.

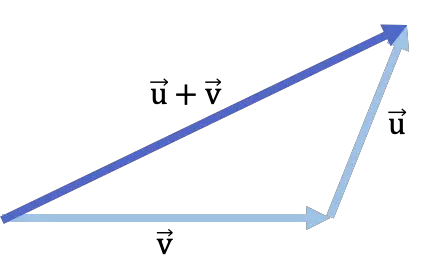
طريقة الرأس والذيل

طريقة الرأس والذيل ، أو المعروفة أيضًا باسم طريقة المثلث ، هي إجراء آخر يمكن من خلاله إضافة متجهين بيانيًا. وفي هذه الحالة فإن الخطوات التي يجب اتباعها هي:

انقل المتجه المضاف وضعه بحيث يكون أصله عند نهاية المتجه المضاف الآخر.
نتيجة إضافة المتجه هي القطعة التي تمتد من بداية المتجه المضاف الأول إلى نهاية المتجه الآخر. إذا نظرت عن كثب، ستجد أن المثلث قد اكتمل بإضافة المتجهين وإضافة المتجه.

فيما يلي مثال على إضافة المتجهات باستخدام طريقة الرأس إلى الذيل:

طريقة المضلع

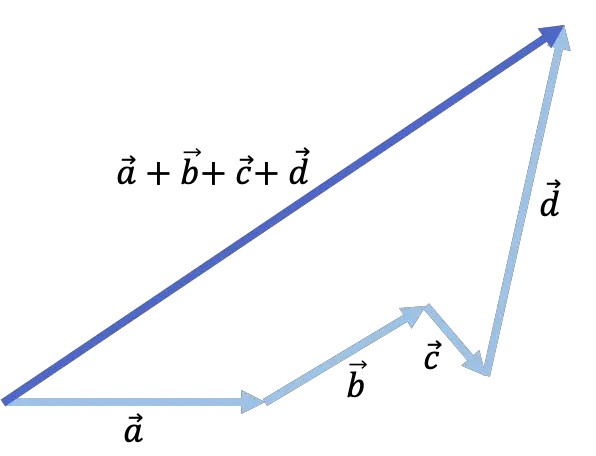
بمجرد أن رأينا كيفية حل مجموع متجهين بيانيًا، سنرى كيف يتم ذلك عندما يكون لدينا أكثر من متجهين.

عندما تريد إضافة ثلاثة متجهات أو أكثر، هناك تقنية لتسريع حساب العملية. تسمى هذه التقنية بطريقة المضلع وتتكون من تطبيق طريقة الرأس إلى الذيل بشكل متتابع:

علينا أولًا وضع كل متجه بعد الآخر، بحيث يتطابق أصل أحد المتجهين مع نهاية متجه آخر. الترتيب الذي نضعهم فيه غير مهم.
ونتيجة الجمع هي المتجه الذي يتم الحصول عليه من خلال ربط بداية المتجه الأول بنهاية المتجه الأخير.

انظر إلى المثال التالي حيث تمت إضافة 4 ناقلات:

كيفية العثور على مجموع طريقة مضلع المتجهات

حساب مجموع متجهين عدديا

بمجرد أن نعرف كيفية جمع المتجهات هندسيًا، سنرى كيفية حساب مجموع المتجهات عدديًا أو جبريًا.

لإضافة متجهين عدديًا، يجب عليك إضافة مكونات كل منهما. أو بمعنى آخر، يتم إضافة إحداثيات X للمتجهين إلى بعضها البعض ونفس إحداثيات Y.

$\vv{\text{u}} = (\text{u}_x,\text{u}_y) \qquad \vv{\text{v}}=(\text{v}_x, \text{v}_y)$

$\vv{\text{u}} + \vv{\text{v}} = (\text{u}_x + \text{v}_x \ , \ \text{u}_y + \text{v}_y)$

على سبيل المثال، المجموع بين المتجهات

$\vv{\text{u}} = (1,2)$

$\vv{\text{v}}=(5, 3)$

شرق:

$\vv{\text{u}} = (1,2) \qquad \vv{\text{v}}=(5, 3)$

$\begin{aligned} \vv{\text{u}} + \vv{\text{v}}& =(1,2) +(5, 3) \\[2ex] & = (1+5,2+3) \\[2ex] & = \bm{(6,5)} \end{aligned}$

ومن ناحية أخرى، يجب أن نضع في اعتبارنا أن جمع المتجهات لمتجهين ليس هو نفس جمع وحدات المتجهات، في الواقع النتائج مختلفة تمامًا. يمكنك رؤية الاختلافات بين العمليتين في خصائص حجم المتجه (وتسمى أيضًا حجم المتجه).

إضافة خصائص المتجهات

تتميز إضافة المتجهات بالخصائص التالية:

الخاصية الترابطية : وضع الأقواس بين مجموع عدة متجهات لا يغير نتيجة العملية.

$\vv{a} + (\vv{b} + \vv{c}) = (\vv{a}+\vv{b})+ \vv{c}$

الخاصية التبادلية – على عكس طرح المتجهات، تكون نتيجة الجمع بين متجهين مستقلة عن ترتيب إضافتهما.

$\vv{a} + \vv{b} = \vv{b}+\vv{a}$

خاصية العنصر المقابل : مجموع المتجه زائد ضده، أي سالبه، يساوي 0.

$\vv{a} +(- \vv{a}) =0$

خاصية العنصر المحايد : من الواضح أن أي متجه بالإضافة إلى المتجه الفارغ أو الفارغ يعادل المتجه نفسه:

$\vv{a} +0 = \vv{a}$

حل مشاكل إضافة المتجهات

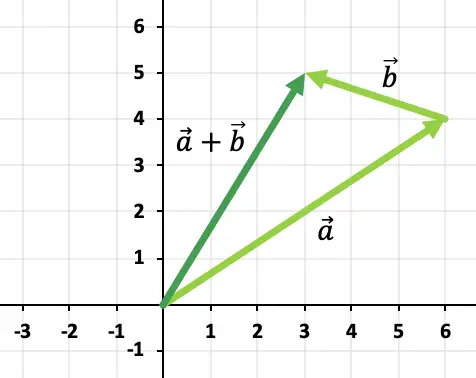
التمرين 1

حساب مجموع المتجهات بيانيا

$\vv{a}$

$\vv{b}:$

انظر الحل

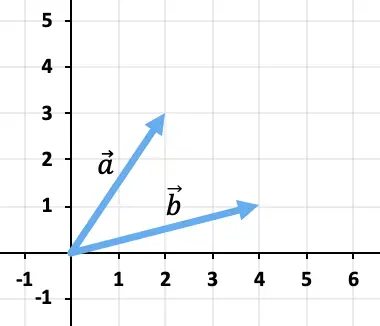
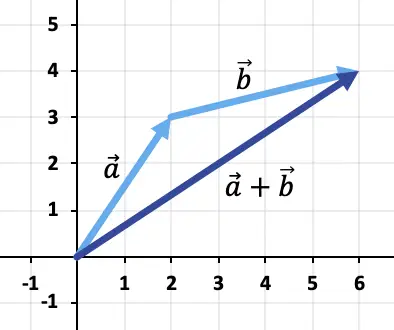
لجمع المتجهين، سنستخدم قاعدة الرأس والذيل. ولذلك، فإننا سوف نضع أصل المتجه

$\vv{b}$

في نهاية المتجه

$\vv{a}$

، وسيكون المجموع هو المتجه الذي يمتد من أصل الإحداثيات إلى نهايته

$\vv{b}.$

وبالتالي فإن نتيجة إضافة المتجهات هي:

تمرين 2

حل مجموع المتجهات بيانيا

$\vv{a}$

$\vv{b}:$

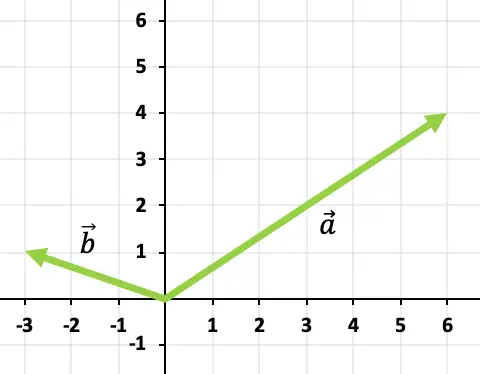
تم حل التمرين خطوة بخطوة بالإضافة إلى المتجهات

انظر الحل

لجمع المتجهين، سنستخدم قاعدة الرأس والذيل. وبالتالي فإننا سوف نحدد أصل المتجه

$\vv{b}$

في نهاية المتجه

$\vv{a}$

، وسيكون متجه المجموع هو الذي يمتد من أصل المحاور إلى نهايتها

$\vv{b}.$

وبالتالي فإن نتيجة إضافة المتجهات هي:

التمرين 3

حدد بيانياً المتجه الناتج عن جمع جميع المتجهات الممثلة في الرسم البياني:

انظر الحل

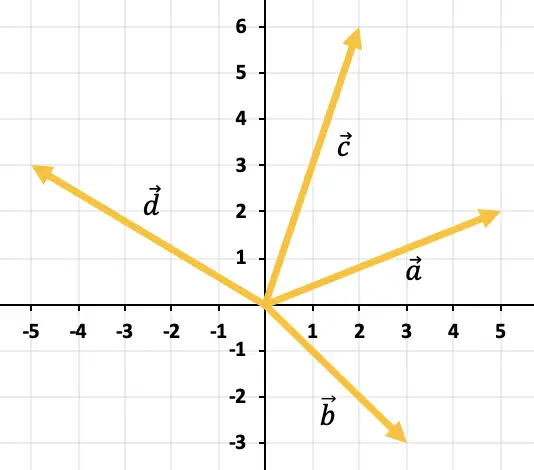
لإضافة أكثر من متجهين من الرسم البياني، يجب عليك استخدام قاعدة المضلع. ولذلك يجب علينا تحريك المتجهات بحيث تظل مستمرة، أي واحدًا تلو الآخر (الترتيب غير ذي صلة). إذن، مجموع كل المتجهات سيكون المتجه الذي يبدأ من أصل المتجه الأول إلى نهاية المتجه الأخير.

وبالتالي فإن نتيجة مجموع المتجهات الأربعة هو المتجه الممثل باللون الأحمر:

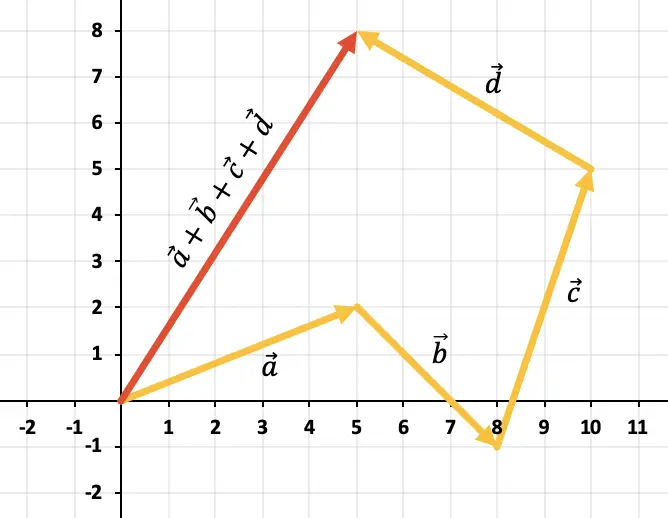
التمرين 4

أوجد عددياً مجموع المتجهات التالية:

$\vv{a}=(3,-2) \qquad \vv{b}=(-4,6)$

انظر الحل

لإضافة متجهين عدديًا، يجب عليك إضافة إحداثيات كل منهما:

$\begin{aligned} \vv{a}+\vv{b}& =(3,-2)+(-4,6) \\[2ex] & = (3+(-4) ,-2+6)\\[2ex] & =\bm{(-1,4)} \end{aligned}$

التمرين 5

حساب تحليليا مجموع المتجهات التالية:

$\vv{a}=(-1,3) \qquad \vv{b}=(4,0)\qquad \vv{c}=(2,-5)\qquad \vv{b}=(3,-2)$

انظر الحل

لإضافة المتجهات عدديًا، يجب عليك إضافة إحداثياتها الخاصة:

$\begin{aligned} \vv{a}+\vv{b}+\vv{c}+\vv{d}& =(-1,3)+(4,0)+(2,-5)+(3,-2) \\[2ex] & = (3,3)+(2,-5)+(3,-2) \\[2ex] & = (5,-2)+(3,-2)\\[2ex] & =\bm{(8,-4)} \end{aligned}$

كيفية إضافة ناقلين بيانيا؟

طريقة أو قاعدة متوازي الأضلاع

طريقة الرأس والذيل

طريقة المضلع

حساب مجموع متجهين عدديا

إضافة خصائص المتجهات

حل مشاكل إضافة المتجهات

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

اترك تعليقاً إلغاء الرد