▷ نظرية الباقي: ماهيتها والأمثلة والتدريبات المحلولة ✅

ستجد هنا شرحًا لماهية نظرية الباقي (أو نظرية الباقي) وكيفية تطبيقها على كثيرات الحدود. ستتمكن أيضًا من رؤية الأمثلة، بالإضافة إلى التدرب على حل التمارين خطوة بخطوة حول نظرية الباقي.

ما هي نظرية الباقي؟

في الرياضيات، تنص نظرية الباقي على أن باقي قسمة أي كثيرة الحدود P(x) على كثيرة حدود أخرى من الشكل (xa) يساوي القيمة العددية لكثيرة الحدود P(x) للقيمة x=a، في بمعنى آخر، باقي القسمة P(x):(xa) يعادل P(a).

مثال على نظرية الباقي

بعد أن رأينا ما هي نظرية الباقي، دعونا نلقي نظرة على مثال عملي لتطبيقها:

احسب باقي القسمة بين كثيرتي الحدود التاليتين:

$P(x) = x^3+2x^2-4x+3 \qquad \qquad Q(x)=x-1$

$\cfrac{P(x)}{Q(x)}$

للعثور على باقي (أو بقايا) تقسيم كثيرات الحدود يمكننا الاستفادة من نظرية الباقي، لأنه في هذه الحالة يكون كثير الحدود المقسوم على الشكل (xa)، أي أنه من الدرجة الأولى، معامل المتغير x هو 1 وله حد مستقل.

لذلك نطبق نظرية الباقي، التي تنص على أن باقي القسمة مثل هذه يساوي القيمة العددية لمقسومة كثيرة الحدود مقيمة في الحد المستقل لكثيرة الحدود المقسوم عليها المتغيرة، أي P (1).

لذلك، لإيجاد باقي القسمة، نحتاج إلى تقييم كثيرة الحدود عند x=1:

$\begin{aligned} P(1) &= 1^3+2\cdot 1^2-4\cdot 1+3\\[2ex] &= 1+2\cdot 1-4 \cdot 1+3 \\[2ex] & = 1+2-4+3 \\[2ex] & =\bm{2} \end{aligned}$

وبالتالي فإن باقي القسمة بين كثيرات الحدود هو 2 .

من ناحية أخرى، يمكننا أيضًا التحقق من قاعدة روفيني لتقسيم كثيرات الحدود بحيث يتطابق الباقي مع النتيجة التي وجدناها:

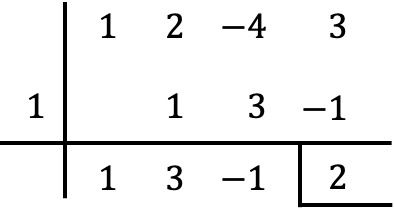
كما ترون، من الأسرع والأسهل تحديد باقي قسمة كثيرة الحدود على ذات الحدين باستخدام نظرية الباقي مقارنة بقاعدة روفيني، لأنه يتم إجراء عدد أقل من العمليات الحسابية.

نظرية الباقي والعامل

من نظرية الباقي وتعريف الجذر (أو الصفر) لكثيرة الحدود يمكننا استنتاج نظرية العامل. لذا فإن نظرية العامل تتضمن ما يلي:

تنص نظرية العوامل على أن كثيرة الحدود P(x) قابلة للقسمة على كثيرة حدود أخرى من الصيغة (xa) إذا، وفقط إذا، P(a)=0. وفي هذه الحالة، هذا يعني أن a هو جذر أو صفر للكثيرة الحدود P(x).

علاوة على ذلك، وفقًا لنظرية الباقي، هذا يعني أنه إذا كانت كثيرة الحدود قابلة للقسمة على كثيرة حدود أخرى، فإن باقي القسمة المذكورة يكون صفرًا، حيث أن P(a)=0.

على سبيل المثال، إذا كان لدينا كثيرة الحدود معينة:

$P(x)=x^2+2x-8$

كثير الحدود هذا قابل للقسمة على الحدين (x-2) لأن P(2)=0:

$\begin{aligned} P(2) &= 2^2+2\cdot 2-8\\[2ex] &= 4+4-8 \\[2ex] & =\bm{0} \end{aligned}$

بما أن x=2 يلغي كثيرة الحدود P(x)، فهذا يعني أن x=2 هو جذر كثير الحدود المذكور.

علاوة على ذلك، بما أن P(2)=0، يمكننا أن نعرف بفضل نظرية الباقي أن باقي القسمة

$\cfrac{x^2+2x-8}{x-2}$

يساوي 0.

حل تمارين نظرية الباقي

لإكمال فهم نظرية الباقي، قمنا بإعداد بعض التمارين التي تم حلها خطوة بخطوة حتى تتمكن من التدرب عليها. ننصحك بتجربة التمرين بنفسك أولاً ثم التحقق مما إذا كنت قد قمت به بشكل صحيح.

التمرين 1

أوجد، باستخدام نظرية الباقي، باقي قسمة كثيرات الحدود

$\cfrac{P(x)}{Q(x)}$

، كونها كثيرات الحدود المشاركة في العملية:

$P(x) =x^3+4x^2-2x+1\qquad \qquad Q(x)=x-2$

انظر الحل

تتكون كثيرة الحدود المقسوم عليها فقط من حد من الدرجة الأولى وحد مستقل، علاوة على ذلك، فإن معامل حد الدرجة الأولى هو 1. وبالتالي يمكننا استخدام نظرية الباقي.

ولتطبيق نظرية الباقي، يكفي تقييم مقسوم كثير الحدود في الحد المستقل لعلامة كثير الحدود المتغيرة، أو بمعنى آخر، يجب علينا حساب P(2).

$\begin{aligned} P(2) &= 2^3+4\cdot 2^2-2\cdot 2+1\\[2ex] &=8+4\cdot 4-2\cdot 2+1 \\[2ex] & = 8+16-4+1 \\[2ex] & =\bm{21} \end{aligned}$

وبالتالي فإن ما تبقى من التقسيم بين كثيرتي الحدود هو 21 .

تمرين 2

بالنظر إلى كثير الحدود

$P(x)=x^4-2x^3+5x^2-3x+4 ,$

أوجد الباقي الذي تم الحصول عليه بقسمته على كل من كثيرات الحدود التالية:

$\text{A)} \ \left(x-1 \right)$
$\text{B)} \ \left(x+1 \right)$
$\text{C)} \ \left(x+2 \right)$
$\text{D)} \ \left(x-3 \right)$

انظر الحل

بما أن جميع متعددات الحدود القابلة للقسمة تستوفي شروط نظرية الباقي، فيمكننا استخدام هذه النظرية لتحديد باقي كل قسمة:

$\begin{aligned} \mathbf{A}\bm{)} \ P(1) &= 1^4-2\cdot 1^3+5\cdot 1^2-3\cdot 1+4\\[2ex] &=1-2\cdot 1+5\cdot 1 -3 \cdot 1+4 \\[2ex] & = 1-2+5-3+4 \\[2ex] & =\bm{5} \end{aligned}$

$\begin{aligned} \mathbf{B}\bm{)} \ P(-1) &= (-1)^4-2\cdot (-1)^3+5\cdot (-1)^2-3\cdot (-1)+4\\[2ex] &=1-2\cdot (-1)+5\cdot 1 -3 \cdot (-1)+4 \\[2ex] & = 1+2+5+3+4 \\[2ex] & =\bm{15} \end{aligned}$

$\begin{aligned} \mathbf{C}\bm{)} \ P(-2) &= (-2)^4-2\cdot (-2)^3+5\cdot (-2)^2-3\cdot (-2)+4\\[2ex] &=16-2\cdot (-8)+5\cdot 4 -3 \cdot (-2)+4 \\[2ex] & = 16+16+20+6+4 \\[2ex] & =\bm{62} \end{aligned}$

$\begin{aligned} \mathbf{D}\bm{)} \ P(3) &= 3^4-2\cdot 3^3+5\cdot 3^2-3\cdot 3+4\\[2ex] &=81-2\cdot 27+5\cdot 9 -3 \cdot 3+4 \\[2ex] & = 81-54+45-9+4 \\[2ex] & =\bm{67} \end{aligned}$

التمرين 3

احسب القيمة التي يجب أن تستحقها المعلمة

$m$

بحيث يكون ما تبقى من تقسيم كثيرات الحدود

$\cfrac{P(x)}{Q(x)}$

تكون مساوية لـ 3، وكلاهما متعددو الحدود:

$P(x) =x^3-5x^2-mx+9 \qquad \qquad Q(x)=x+3$

انظر الحل

في هذه الحالة تحديدًا، تتكون كثيرة حدود القسمة من أحادية الحد من الدرجة الأولى وحد مستقل، علاوة على ذلك، فإن معامل أحادية الحد من الدرجة الأولى هو 1. وبالتالي يمكننا استخدام نظرية الباقي.

ولاستخدام نظرية الباقي، ما عليك سوى استبدال الحد المستقل لكثيرة الحدود المقسومة بتغيير الإشارة حيث يوجد في كثير الحدود المقسومة x، لذا يجب علينا حل P(-3).

$\begin{aligned} P(-3) &=(-3)^3-5\cdot (-3)^2-m\cdot (-3)+9\\[2ex] &=-27-5\cdot 9 -m\cdot (-3)+9 \\[2ex] & = -27-45+3m+9 \\[2ex] & =3m-63 \end{aligned}$