منتج مختلط لثلاثة ناقلات (أو منتج ثلاثي النقاط)

نوضح في هذه الصفحة ما هو حاصل الضرب المختلط لثلاثة ناقلات (أو حاصل الضرب الثلاثي) وكيف يتم حسابه. سترى أيضًا أمثلة وتمارين ومسائل تم حلها حول هذا النوع من العمليات بين المتجهات. وبالإضافة إلى ذلك، سوف تجد خصائص وتطبيقات المنتج المختلط.

ما هو المنتج المختلط لثلاثة ناقلات؟

الضرب المختلط لثلاثة ناقلات، ويسمى أيضًا حاصل الضرب النقطي الثلاثي ، هو ضرب متتابع بين ثلاثة ناقلات يتضمن نوعين مختلفين من العمليات: حاصل الضرب النقطي وحاصل الضرب المتجه . لذلك، فإن الجمع بين العمليتين المتجهتين يعطي رقمًا قياسيًا (عددًا حقيقيًا).

بشكل ملموس، يتكون المنتج المختلط من حساب المنتج المتجه لمتجهين، وبالتالي ضرب النتيجة التي تم الحصول عليها بواسطة ناقل ثالث. قد يبدو الأمر معقدًا جدًا عند كتابته بهذه الطريقة، لكنه في الواقع ليس كثيرًا، انظر إلى صيغة منتج النقاط الثلاثية:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})$

كما ترون في صيغته، يُشار إلى حاصل الضرب المختلط لثلاثة متجهات بقوسين مربعين.

كيفية حساب المنتج المختلط لثلاثة ناقلات؟

صيغة حاصل الضرب الثلاثي هي التي رأيناها للتو في القسم السابق، ومع ذلك، لا يتم استخدامها بشكل عام لتحديد حاصل الضرب المختلط لثلاثة ناقلات لأن هناك طريقة أخرى أبسط وأسرع:

دع أي 3 ناقلات تكون:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)\qquad \vv{\text{w}}= (\text{w}_x,\text{w}_y,\text{w}_z)$

لحساب حاصل الضرب المختلط بين ثلاثة متجهات، ما عليك سوى حل المحدد 3×3 الذي يتكون من مكونات المتجهات:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \\[1.1ex] \text{w}_x & \text{w}_y & \text{w}_z \end{vmatrix}$

لذا يمكنك أن ترى مثالاً لكيفية حساب ذلك ، وسوف نجد المنتج المختلط للمتجهات الثلاثة التالية:

$\vv{\text{u}}= (1,2,0) \qquad \vv{\text{v}}= (0,-1,3)\qquad \vv{\text{w}}= (-2,4,1)$

لتحديد حاصل الضرب المختلط، نقوم ببناء محدد من الرتبة 3 عن طريق وضع المتجهات في صفوف المصفوفة:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]=\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix}$

والآن نحتاج فقط إلى حل محدد المصفوفة، ولهذا يمكنك استخدام أي طريقة. في هذه الحالة، سوف نطبق قاعدة ساروس (ولكن يمكن القيام بذلك أيضًا عن طريق الإضافات أو العوامل المساعدة):

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 1 & 2 & 0 \\[1.1ex] 0 & -1 & 3 \\[1.1ex] -2 & 4 & 1 \end{vmatrix} \\[2ex] &= -1-12+0-0-12-0 \\[2ex] & = \bm{-25} \end{aligned}$

ولإظهار أن الإجراءين متكافئين، سنحسب المنتج المختلط لنفس المتجهات عن طريق تعريفها:

$\begin{aligned} \bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] & = \vv{\text{u}} \cdot ( \vv{\text{v}}\times \vv{\text{w}})\\[2ex] &=(1,2,0) \cdot \Bigl( (0,-1,3)\times (-2,4,1)\Bigr) \\[2ex] & = (1,2,0) \cdot \begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 0& -1 & 3 \\[1.1ex] -2 &4&1 \end{vmatrix} \\[2ex] &= (1,2,0) \cdot (-13,-6,-2) \\[2ex] & = \bm{-25} \end{aligned}$

نوصي بحساب حاصل الضرب المختلط من خلال محدد المتجهات، لأنه أسرع واحتمال ارتكاب الأخطاء أقل. ولكن، كما ترى، النتيجة هي نفسها بغض النظر عن الطريقة التي تستخدمها، لذا استخدم الطريقة التي تفضلها. 👍

التفسير الهندسي للمنتج المختلط

بمجرد أن تعرف كيفية العثور على المنتج المختلط لثلاثة ناقلات، قد تتساءل… وما هو المنتج المختلط؟ حسنًا، في الرياضيات له استخدامان رئيسيان: حساب حجم متوازي السطوح وحجم رباعي السطوح.

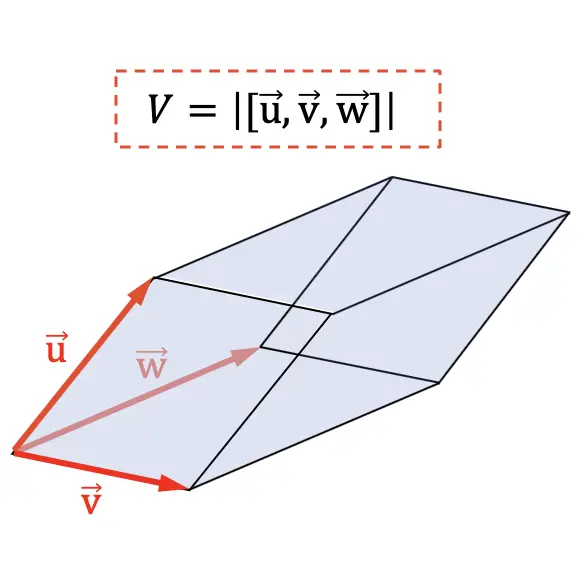
حجم متوازي السطوح يساوي القيمة المطلقة للمنتج المختلط للمتجهات التي تحدد الأبعاد الثلاثة للمجال الهندسي.

مثال على المنتج المختلط لثلاثة ناقلات أو المنتج العددي الثلاثي

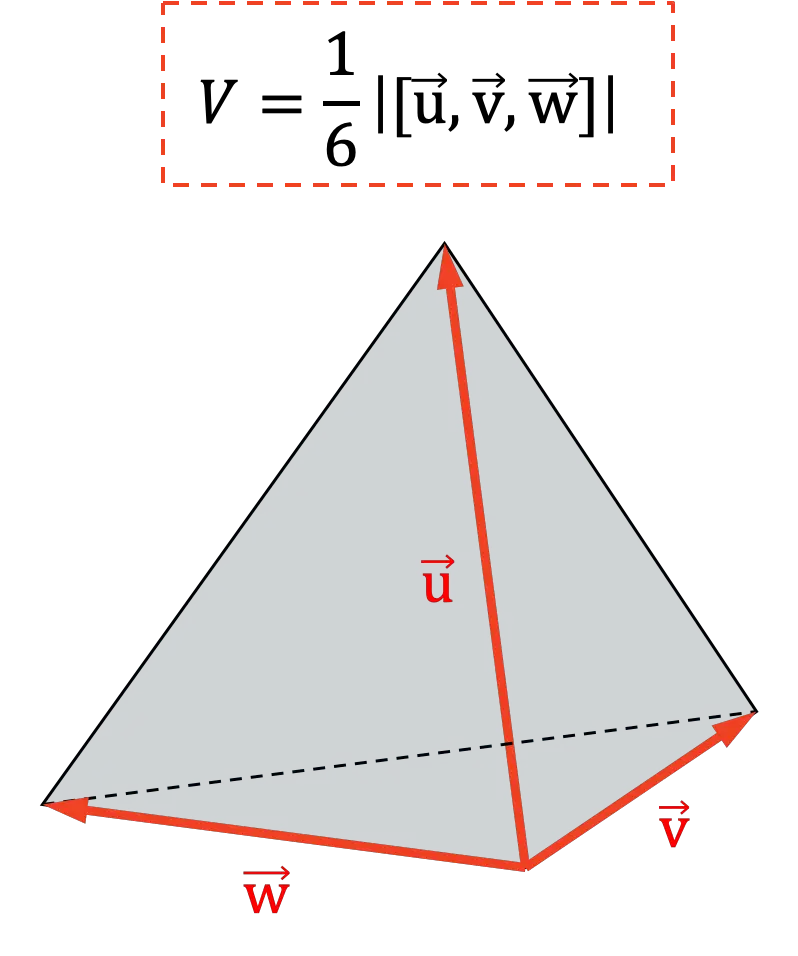
تطبيق آخر للمنتج المختلط هو تحديد حجم رباعي الاسطح . بما أن الجزء السادس من القيمة المطلقة للمنتج المختلط هندسيًا يمثل حجم رباعي السطوح:

خصائص المنتج المختلط أو منتج النقاط الثلاثية

يتميز المنتج المختلط أو المنتج العددي الثلاثي بالخصائص التالية:

بشكل عام، التغيير في ترتيب ناقلات المنتجات المختلطة يعني أيضًا تغييرًا في الإشارة. ولذلك، فإن ترتيب ناقلات المنتجات المختلطة مهم.

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{v}},\vv{\text{u}},\vv{\text{w}}\bigr] = -\bigl[\vv{\text{u}},\vv{\text{w}},\vv{\text{v}}\bigr] = - \bigl[\vv{\text{w}},\vv{\text{v}},\vv{\text{u}}\bigr]$

ومع ذلك، إذا قمنا بتغيير الترتيب بشكل دوري ، فإن الإشارة لا تتغير:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr] = \bigl[\vv{\text{v}},\vv{\text{w}},\vv{\text{u}}\bigr] = \bigl[\vv{\text{w}},\vv{\text{u}},\vv{\text{v}}\bigr]$

في الفضاء ثلاثي الأبعاد (في R3)، يساوي المنتج المختلط لثلاثة ناقلات تعتمد خطيًا أو متحدة المستوى (تنتمي إلى نفس المستوى) 0.

تم إصلاح مشكلات المنتجات المختلطة

التمرين 1

نظرا لثلاثة ناقلات:

$\vv{\text{u}}= (3,-1,2) \qquad \vv{\text{v}}= (-2,0,1)\qquad \vv{\text{w}}= (5,1,-1)$

احسب المنتج المختلط للنواقل الثلاثة:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

انظر الحل

للعثور على منتجها المختلط، يجب علينا حل المحدد المكون من إحداثيات المتجهات:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 3 & -1 & 2 \\[1.1ex] -2 & 0 & 1 \\[1.1ex] 5 & 1 & -1 \end{vmatrix} \\[2ex] &= 0-5-4-0-3+2 \\[2ex] & = \bm{-10} \end{aligned}$

تمرين 2

نظرا لثلاثة ناقلات:

$\vv{\text{u}}= (7,2,-3) \qquad \vv{\text{v}}= (2,4,9)\qquad \vv{\text{w}}= (4,3,-1)$

تحديد المنتج المختلط بين المتجهات الثلاثة:

$\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]$

انظر الحل

لإيجاد حاصل ضربها المختلط، علينا إيجاد المحدد الذي له الإحداثيات الديكارتية للمتجهات في صورة خطية:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 7 & 2 & -3 \\[1.1ex] 2 & 4 & 9 \\[1.1ex] 4 & 3 & -1 \end{vmatrix} \\[2ex] &= -28+72-18+48-189+4 \\[2ex] & = \bm{-111} \end{aligned}$

التمرين 3

احسب حجم متوازي السطوح الذي أضلاعه الثلاثة هي المتجهات التالية:

$\vv{\text{u}}= (0,2,5) \qquad \vv{\text{v}}= (-1,6,2)\qquad \vv{\text{w}}= (3,1,2)$

انظر الحل

حجم متوازي السطوح يساوي القيمة المطلقة لحاصل الضرب المختلط لثلاثة من المتجهات التي له حواف. لذلك، نحسب أولًا حاصل الضرب الثلاثي للمتجهات:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 0 & 2 & 5 \\[1.1ex] -1 & 6 & 2 \\[1.1ex] 3 & 1 & 2 \end{vmatrix} \\[2ex] &= 0+12-5-90-0+4 \\[2ex] & = -79 \end{aligned}$

بحيث يكون حجم الموازي هو القيمة المطلقة لنتيجة المنتج المختلط:

$V= \lvert -79 \rvert = \bm{79}\ \mathbf{u}\bm{^3}$

التمرين 4

احسب حجم الشكل الرباعي الذي رؤوسه النقاط التالية:

$A(1,0,2) \qquad B(3,3,2)\qquad C(5,-1,4)\qquad D(4,2,1)$

انظر الحل

أولاً، نحسب المتجهات التي تمثل حواف رباعي الأسطح:

$\vv{AB}=B-A= (3,3,2)-(1,0,2)=(2,3,0)$

$\vv{AC}=C-A= (5,-1,4)-(1,0,2)=(4,-1,2)$

$\vv{AD}=D-A= (4,2,1)-(1,0,2)=(3,2,-1)$

حجم رباعي السطوح يعادل سدس القيمة المطلقة للمنتج المختلط لثلاثة من المتجهات الموجودة في الحواف. لذلك، نقوم أولاً بحساب المنتج المختلط للمتجهات الموجودة:

$\begin{aligned}\bigl[\vv{\text{u}},\vv{\text{v}},\vv{\text{w}}\bigr]& =\begin{vmatrix} 2 & 3 & 0 \\[1.1ex] 4 & -1 & 2 \\[1.1ex] 3 & 2 & -1 \end{vmatrix} \\[2ex] &= 2+18+0-0-8+12 \\[2ex] & = 24 \end{aligned}$

وبالتالي فإن حجم رباعي السطوح سيكون سدس القيمة المطلقة للمنتج المختلط:

$V= \cfrac{1}{6} \cdot \lvert 24 \rvert = \cfrac{24}{6} = \bm{4} \ \mathbf{u}\bm{^3}$

ما هو المنتج المختلط لثلاثة ناقلات؟

كيفية حساب المنتج المختلط لثلاثة ناقلات؟

التفسير الهندسي للمنتج المختلط

خصائص المنتج المختلط أو منتج النقاط الثلاثية

تم إصلاح مشكلات المنتجات المختلطة

التمرين 1

تمرين 2

التمرين 3

التمرين 4

اترك تعليقاً إلغاء الرد