▷ حساب المنتج المتقاطع لمتجهين (أمثلة)

تشرح هذه الصفحة ما هو حاصل الضرب الاتجاهي لمتجهين وكيفية حسابه. سترى أيضًا كيفية العثور على اتجاه واتجاه حاصل الضرب المتقاطع باستخدام قاعدة اليد اليمنى (أو المفتاح). والأكثر من ذلك، ستجد استخدامات هذا النوع من العمليات، بالإضافة إلى أمثلة وتمارين ومسائل تم حلها خطوة بخطوة.

ما هو المنتج المتقاطع لمتجهين؟

في الرياضيات، المنتج المتقاطع هو عملية بين متجهين في الفضاء ثلاثي الأبعاد (في R3). نتيجة عملية المتجه هذه هي متجه ذو اتجاه عمودي على المتجهين المضربين، وبوحدة تساوي حاصل ضرب وحدات المتجهات المضاعفة في جيب الزاوية التي يشكلونها. وبعبارة أخرى فإن صيغته هي:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

كما ترون في الصيغة السابقة، تتم الإشارة إلى المنتج الاتجاهي

$\bm{\times}$

ولهذا السبب يطلق عليه أيضًا المنتج المتقاطع. يُطلق عليه أيضًا أحيانًا اسم منتج Gibbs المتجه، منذ أن اخترعه.

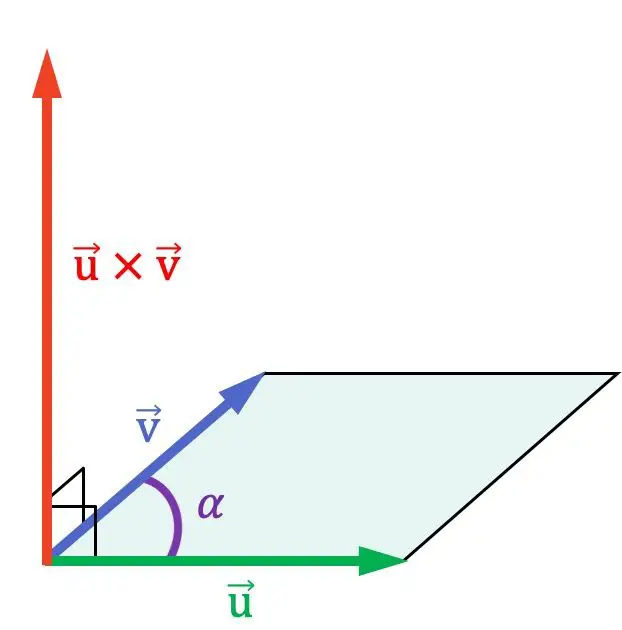
كما ترون في التمثيل البياني السابق، فإن حاصل الضرب الاتجاهي يكون عموديًا على المتجهين اللذين يضربانهما، وبالتالي، فهو عمودي على المستوى الذي يحتويهما.

صيغة لحساب المنتج المتقاطع لمتجهين

إذا كنا نعرف الإحداثيات الديكارتية للمتجهات، فإن أبسط طريقة لحساب حاصل الضرب الاتجاهي لها هي إيجاد محدد 3×3. شاهد كيف يتم ذلك:

خذ بعين الاعتبار أي متجهين:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

منتجها المتجه هو:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

حيث النواقل

$\vv{i}, \vv{j},\vv{k}$

هذه هي متجهات الوحدة في اتجاهات المحاور X وY وZ على التوالي.

دعونا نرى مثالاً لكيفية حساب حاصل الضرب الاتجاهي بين متجهين:

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

لتحديد حاصل الضرب المتجه بين المتجهات، يجب علينا عمل المحدد التالي من الرتبة 3:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

في هذه الحالة، سوف نقوم بحل المحدد بواسطة العوامل المساعدة أو العوامل المساعدة (يمكن أيضًا استخدام قاعدة ساروس):

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

وبالتالي فإن نتيجة المنتج المتجه للمتجهين هي:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

يحدد اتجاه واتجاه المنتج المتقاطع

في بعض الأحيان لا نحتاج إلى معرفة مركبات المتجه الناتج عن حاصل الضرب الاتجاهي، لكن يكفي إيجاد وحدته واتجاهه واتجاهه. يحدث هذا غالبًا في الفيزياء، خاصة في حساب القوى.

وبالتالي، هناك عدة قواعد للعثور على اتجاه واتجاه المنتج المتجه، وأشهرها هي قاعدة اليد اليمنى ، إما بثلاثة أصابع أو باليد بأكملها، وقاعدة المفتاح (أو المسمار) . يمكنك استخدام أي منها، لذا لا تحتاج إلى معرفتها جميعًا، سنستمر في شرح القواعد الثلاثة لك حتى تتمكن من الالتزام بالقواعد التي تفضلها. 😉

قاعدة اليد اليمنى (3 أصابع)

تتضمن النسخة المكونة من 3 أصابع من قاعدة أو قانون اليد اليمنى تنفيذ الخطوات التالية:

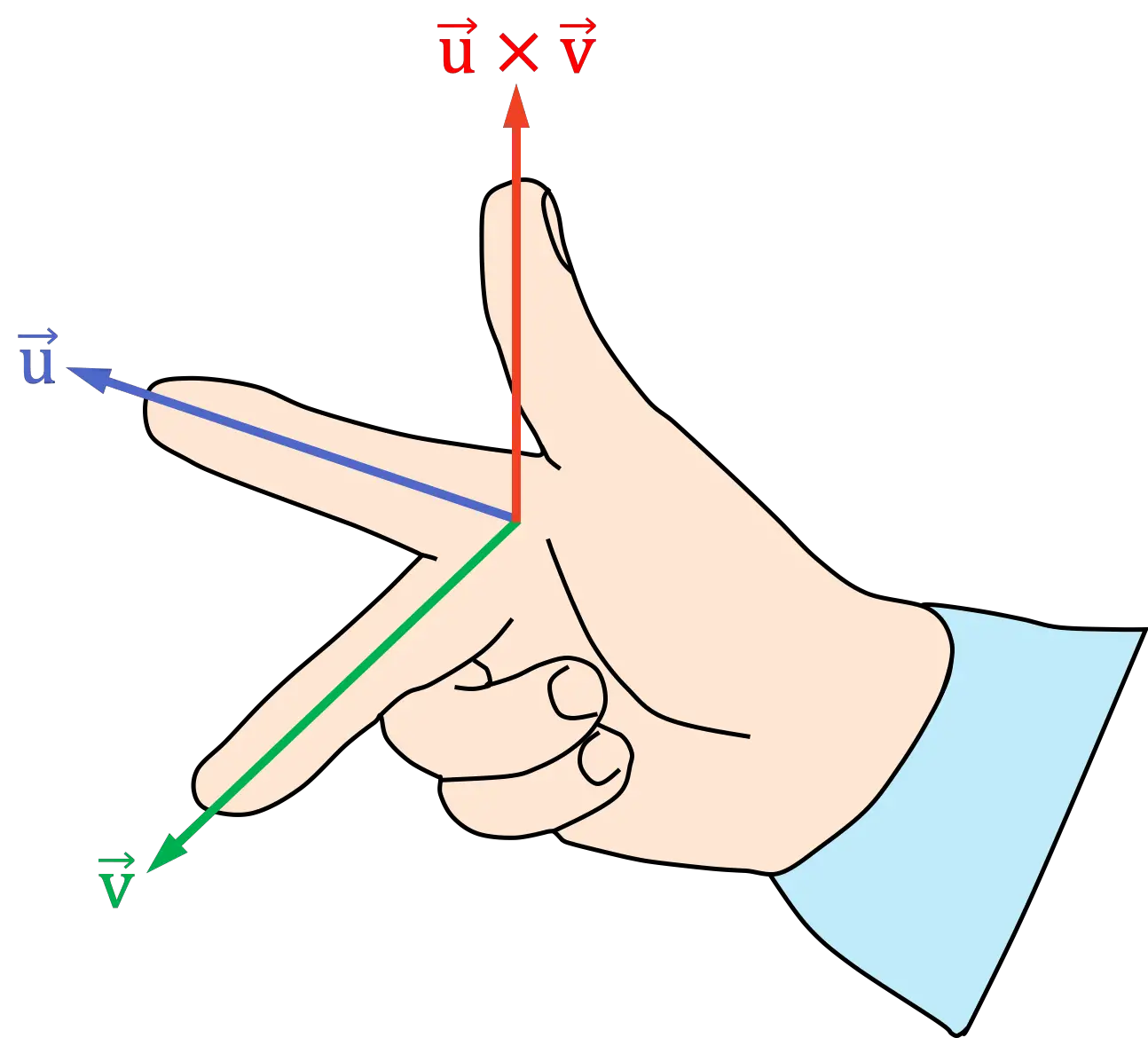
ضع إصبع السبابة بيدك اليمنى باتجاه المتجه الأول لحواصل الضرب
$(\vv{\text{u}}).$
ضع الإصبع الأوسط (أو الإصبع الأوسط) ليدك اليمنى باتجاه المتجه الثاني للمنتج المتقاطع
$(\vv{\text{v}}).$
يشير موضع الإبهام الناتج إلى اتجاه واتجاه المنتج المتقاطع
$(\vv{\text{u}}\times\vv{\text{v}}).$

قاعدة اليد اليمنى (كف اليد)

النسخة الراحية من قاعدة أو قانون اليد اليمنى تشبه إلى حد كبير القاعدة السابقة. ولتطبيقه عليك اتباع الخطوات التالية:

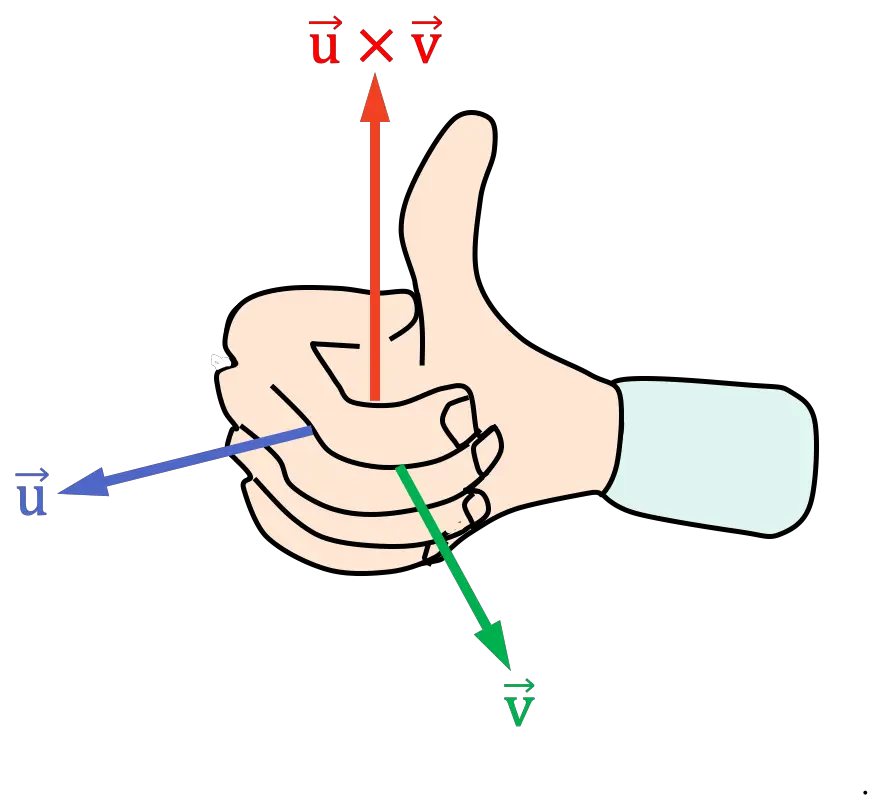
ضع يدك اليمنى مشيرة بأصابعك في نفس اتجاه المتجه الأول لحواصل الضرب
$(\vv{\text{u}}).$
أغلق يدك اليمنى عن طريق تحريك أصابعك نحو المتجه الثاني لحواصل الضرب
$(\vv{\text{v}}).$

تحتاج إلى إغلاق يدك على الجانب الذي تكون فيه الزاوية (أو المسافة) بين المتجهات أصغر.
يحدد موضع الإبهام الناتج اتجاه المنتج المتقاطع
$(\vv{\text{u}}\times\vv{\text{v}}).$

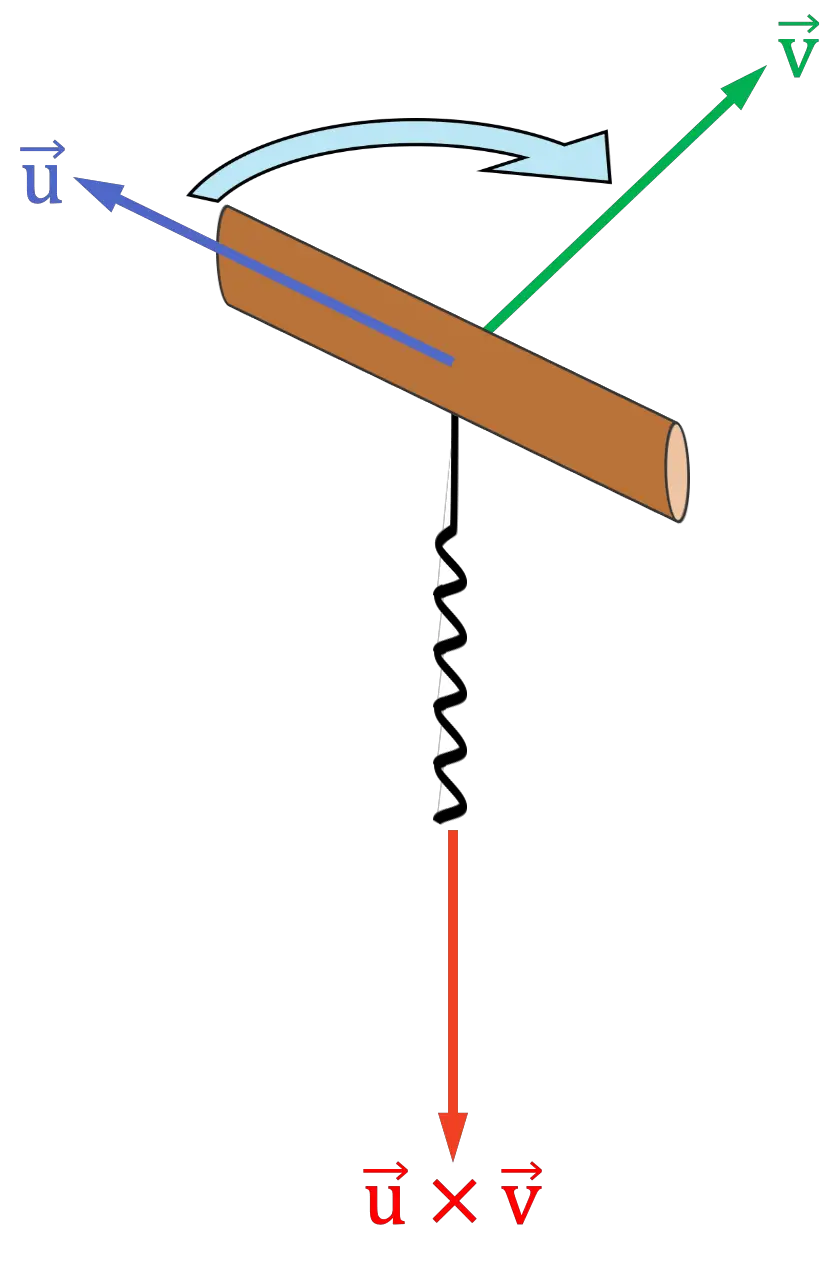
قاعدة المفتاح

تشبه قاعدة المفتاح أو المسمار قاعدة اليد اليمنى باستخدام راحة اليد بأكملها. الإجراء هو كما يلي:

باستخدام خيالك، ضع مفتاحًا (أو برغيًا) بحيث يشير المقبض إلى نفس اتجاه المتجه الأول للمنتج المتقاطع.
$(\vv{\text{u}}).$
ثم أدر المفتاح نحو المتجه الثاني للمنتج المتقاطع
$(\vv{\text{v}})$

كما لو كنت ستضعه في الفلين. تحتاج إلى تحويل المفتاح إلى الجانب الذي تكون فيه المسافة بين المتجهات أقصر.
الاتجاه الذي ستكون فيه النقاط الحلزونية للمفتاح هو اتجاه واتجاه المنتج المتجه
$(\vv{\text{u}}\times\vv{\text{v}}).$

خصائص المنتج المتقاطع لمتجهين

يتميز المنتج المتقاطع لمتجهين بالخصائص التالية:

خاصية مضادة للتبديل: ترتيب المتجهات الداخلة في المنتج المتجه لا يختلف، لأن الإشارة تختلف باختلافه.

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

خاصية التوزيع فيما يتعلق بجمع وطرح المتجهات:

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

خاصية التجانس : ضرب متجه حاصل الضرب الاتجاهي في عدد قياسي (عدد حقيقي) يعادل ضرب نتيجة حاصل الضرب الاتجاهي في العدد القياسي المذكور.

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

المتجه الناتج عن المنتج المتجه يكون متعامدًا مع المتجهين المشاركين في العملية.

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

علاوة على ذلك، إذا كان المتجهان متعامدين، فستتحقق المعادلات التالية:

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

المنتج المتقاطع لمتجهين متوازيين يساوي المتجه الصفري (أو الصفر).

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

إذا كنا لا نعرف الزاوية التي يشكلها متجهان، فيمكن أيضًا حساب معامل حاصل ضربهما المتجه باستخدام التعبير التالي:

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

احسب مساحة متوازي الأضلاع أو المثلث باستخدام حاصل الضرب الاتجاهي

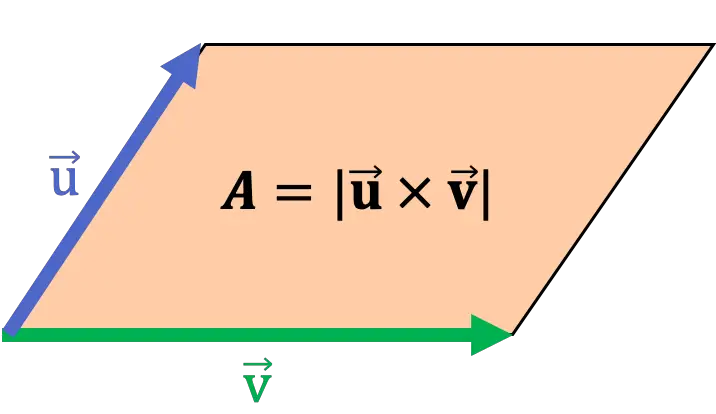
هندسيًا، يتطابق معامل حاصل الضرب العرضي لمتجهين مع مساحة متوازي الأضلاع الذي يحتوي على هذين المتجهين كجوانب. ولذلك، يمكن استخدام المنتج الاتجاهي لحساب مساحة متوازي الأضلاع.

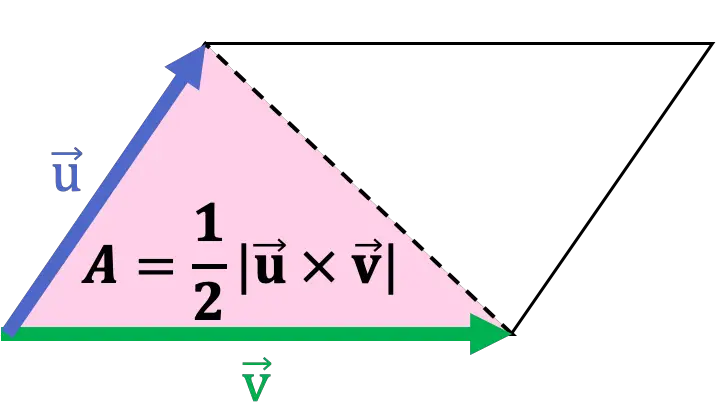
بالإضافة إلى ذلك، فإن قطر متوازي الأضلاع يقسمه إلى مثلثين، أو بمعنى آخر المثلث هو نصف متوازي الأضلاع. وبالتالي، فإن مساحة المثلث هي نصف معامل الضرب الاتجاهي، مع أخذ ضلعين من أضلاعه كمتجهين.

تذكر أن معامل المتجه في فضاء ثلاثي الأبعاد هو جذر مجموع مربعات إحداثياته:

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

هذان اثنان من تطبيقات المنتج المتقاطع لمتجهين في مجال الرياضيات. ومع ذلك، لا يزال له استخدامات أخرى، على سبيل المثال في الفيزياء يتم استخدامه لحساب المجال المغناطيسي.

تمارين محلولة على المنتجات المتجهة للمتجهات

التمرين 1

احسب حاصل الضرب الاتجاهي بين المتجهين التاليين:

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

انظر الحل

لتحديد حاصل الضرب المتجه بين المتجهات، يجب أن نحل محدد البعد التالي 3×3:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

في هذه الحالة، سوف نقوم بحل المحدد بواسطة العوامل المساعدة أو العوامل المساعدة (ولكن يمكن أيضًا استخدام قاعدة ساروس):

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

وبالتالي فإن نتيجة المنتج المتجه للمتجهين هي:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

تمرين 2

أوجد حاصل الضرب الاتجاهي بين المتجهين التاليين:

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

انظر الحل

لإيجاد حاصل ضرب المتجه بين المتجهين، علينا حل المحدد 3×3 التالي:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

في هذه الحالة، سوف نقوم بحساب المحدد من خلال العوامل المجاورة أو العوامل المساعدة (على الرغم من أنه يمكن استخدام قاعدة ساروس بالتبادل):

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

وبالتالي فإن نتيجة منتج المتجه بين المتجهين هي:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

التمرين 3

معرفة وحدات المتجهين والزاوية التي يشكلانها:

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

تحديد حجم المنتج الاتجاهي للمتجهين.

انظر الحل

يمكننا بسهولة حساب معامل منتج المتجه بين المتجهين من خلال تطبيق الصيغة:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

التمرين 4

من المتجهات التالية الموجودة في مستوى الشاشة:

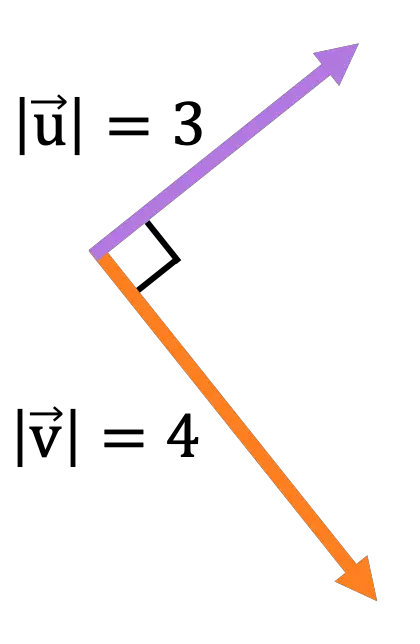
احسب حجم واتجاه وإحساس المتجه الناتج عن عملية المتجه التالية:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

انظر الحل

المتجهان متعامدان، لذا فإن قاعدة حاصل ضرب المتجه ستكون:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

ومن ناحية أخرى، فإن المتجه الناتج عن المنتج المتجه يكون عموديًا على المتجهين المشاركين في العملية، وبالتالي فإن اتجاهه سيكون عموديًا على الشاشة.

وأخيرًا، باستخدام قاعدة الخط المستقيم (أو المفتاح)، يمكننا استنتاج أن اتجاه المتجه الناتج سيكون نحو داخل الشاشة.

التمرين 5

احسب مساحة متوازي الأضلاع الذي يحتوي على المتجهات التالية على شكل ضلعين:

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

انظر الحل

تتطابق مساحة متوازي الأضلاع مع معامل الضرب المتقاطع للمتجهات التي تشكله. لذلك نحسب المنتج المتجه للمتجهات:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

ثم الوحدة الخاصة بك:

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

التمرين 6

أوجد مساحة المثلث الذي تكون رؤوسه النقاط التالية:

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

انظر الحل

أولًا، يجب علينا حساب المتجهات التي تشكل أضلاع المثلث:

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

مساحة المثلث هي نصف حجم المنتج المتجه للمتجهات التي تشكله. لذلك نحسب المنتج المتجه للمتجهات:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

بعد الوحدة الخاصة بك:

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

وأخيرًا، ستكون مساحة المثلث نصف الوحدة:

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

المنتج المتقاطع لمتجهين (أو المنتج المتقاطع)

ما هو المنتج المتقاطع لمتجهين؟

صيغة لحساب المنتج المتقاطع لمتجهين

يحدد اتجاه واتجاه المنتج المتقاطع

قاعدة اليد اليمنى (3 أصابع)

قاعدة اليد اليمنى (كف اليد)

قاعدة المفتاح

خصائص المنتج المتقاطع لمتجهين

احسب مساحة متوازي الأضلاع أو المثلث باستخدام حاصل الضرب الاتجاهي

تمارين محلولة على المنتجات المتجهة للمتجهات

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

اترك تعليقاً إلغاء الرد