كيفية قطري المصفوفة -

ستجد في هذه الصفحة كل شيء عن المصفوفات القابلة للقطر: ما هي، ومتى يمكن قطريًا ومتى لا يمكن ذلك، وطريقة قطري المصفوفات، وتطبيقات وخصائص هذه المصفوفات المعينة، وما إلى ذلك. ولديك أيضًا العديد من التمارين التي تم حلها خطوة بخطوة حتى تتمكن من التدرب على كيفية ترتيبها بشكل قطري وفهمها تمامًا. وأخيرًا، نتعلم أيضًا كيفية إجراء تخطيط قطري للمصفوفات باستخدام برنامج الكمبيوتر MATLAB، نظرًا لأنه يتم استخدامه بشكل متكرر.

ما هي المصفوفة القابلة للقطر؟

كما سنرى أدناه، فإن تحديد المصفوفة بشكل قطري مفيد جدًا في مجال الجبر الخطي. ولهذا السبب يتساءل الكثيرون… ما هو قطري المصفوفة؟ حسنًا، تعريف المصفوفة القابلة للقطر هو:

المصفوفة القابلة للقطر هي مصفوفة مربعة يمكن تحويلها إلى مصفوفة قطرية، أي مصفوفة مملوءة بالأصفار باستثناء القطر الرئيسي. يتم تقسيم قطري المصفوفات على النحو التالي:

$A = PDP^{-1}$

أو ما يعادلها،

$D = P^{-1}AP$

ذهب

$A$

هي المصفوفة لقطري،

$P$

هي المصفوفة التي تكون أعمدتها هي المتجهات الذاتية (أو المتجهات الذاتية) لـ

$A$

$P^{-1}$

مصفوفتها العكسية و

$D$

هي المصفوفة القطرية التي تتكون من القيم الذاتية (أو القيم الذاتية) لـ

$A$

المصفوفة

$P$

تعمل كمصفوفة تغيرات أساسية، لذلك باستخدام هذه الصيغة نقوم بتغيير القاعدة إلى مصفوفة

$A$

، بحيث تصبح المصفوفة مصفوفة قطرية (

$D$

) في القاعدة الجديدة.

ولذلك، المصفوفة

$A$

والمصفوفة

$D$

وهي مصفوفات متشابهة. ومن الواضح،

$P$

إنها مصفوفة عادية أو غير متحللة.

متى يمكنك جعل المصفوفة قطرية؟

لا يمكن جعل جميع المصفوفات قطرية؛ فقط المصفوفات التي تلبي خصائص معينة يمكن أن تكون قطرية. يمكنك معرفة ما إذا كانت المصفوفة قابلة للقطر بطرق مختلفة:

المصفوفة المربعة من الرتبة n تكون قابلة للقطر إذا كانت تحتوي على n ناقلات ذاتية مستقلة خطيًا (أو ناقلات ذاتية) ، أو بمعنى آخر، إذا كانت هذه المتجهات تشكل أساسًا. وذلك لأن المصفوفة
$P$

، والذي يستخدم لقطر المصفوفة، يتكون من المتجهات الذاتية للمصفوفة المذكورة. لمعرفة ما إذا كانت المتجهات الذاتية هي LI، يكفي أن محدد المصفوفة

$P$

يختلف عن 0، مما يعني أن المصفوفة لها أعلى رتبة.

$\text{si} \quad \text{det}(P)\neq 0 \ \longrightarrow \ \text{matriz diagonalizable}$

خاصية القيم الذاتية والمتجهات الذاتية هي أن المتجهات الذاتية ذات القيم الذاتية المختلفة مستقلة خطيًا. لذلك، إذا كانت جميع القيم الذاتية للمصفوفة فريدة من نوعها، تكون المصفوفة قابلة للقطر.

هناك طريقة أخرى لتحديد ما إذا كان يمكن استيعاب المصفوفة في مصفوفة قطرية وهي استخدام التعدديات الجبرية والهندسية. التعددية الجبرية هي عدد المرات التي تتكرر فيها القيمة الذاتية (أو القيمة الذاتية)، والتعددية الهندسية هي بُعد نواة (أو نواة) المصفوفة عن طريق طرح القيمة الذاتية من قطرها الرئيسي. وبالتالي، إذا كان التعدد الجبري لكل قيمة ذاتية يساوي التعدد الهندسي ، فإن المصفوفة قابلة للقطر.

$\alpha_\lambda = \text{multiplicidad algebraica} = \text{multiplicidad del valor propio}$

$m_\lambda = \text{multiplicidad geom\'etrica} = \text{dim } Ker(A-\lambda I) = n -rg(A-\lambda I)$

$\alpha_\lambda \geq m_\lambda \geq 1$

$\text{si} \quad \alpha_\lambda = m_\lambda \quad \forall \lambda \ \longrightarrow \ \text{matriz diagonalizable}$

وأخيرا، هناك نظرية، النظرية الطيفية، التي تضمن قطريا المصفوفات المتماثلة مع الأعداد الحقيقية. بمعنى آخر، أي مصفوفة حقيقية ومتماثلة قابلة للقياس قطريًا .

كيفية قطري المصفوفة

يعتمد الإجراء الخاص بقطر المصفوفة على إيجاد القيم الذاتية (أو القيم الذاتية) والمتجهات الذاتية (أو المتجهات الذاتية) للمصفوفة. ولهذا السبب من المهم أن تتقن كيفية حساب القيم الذاتية (أو القيم الذاتية) والمتجهات الذاتية (أو المتجهات الذاتية) لأي مصفوفة . يمكنك أن تتذكر كيف تم ذلك من خلال النقر على الرابط، حيث نشرح خطوة بخطوة كيفية العثور عليها وبعض الحيل التي تجعل الحسابات أسهل بكثير. بالإضافة إلى ذلك، ستجد أيضًا تمارين محلولة للتدرب عليها.

باستخدام الطريقة التالية، يمكنك تحديد قطري لمصفوفة بأي بعد: 2×2، 3×3، 4×4، إلخ. الخطوات التي يجب اتباعها لتخطيط المصفوفة هي:

الحصول على القيم الذاتية (أو القيم الذاتية) للمصفوفة.
احسب المتجه الذاتي المرتبط بكل قيمة ذاتية.
بناء المصفوفة
$P$

، التي تمثل أعمدتها المتجهات الذاتية للمصفوفة المراد قطرها.
تأكد من أن المصفوفة يمكن أن تكون قطرية (يجب أن تستوفي أحد الشروط الموضحة في القسم السابق).
بناء المصفوفة القطرية
$D$

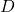
، والتي تكون جميع عناصرها 0 باستثناء العناصر الموجودة على القطر الرئيسي، وهي القيم الذاتية الموجودة في الخطوة 1.

تحذير: المتجهات الذاتية للمصفوفة

$P$

يمكن وضعها بأي ترتيب، ولكن القيم الذاتية للمصفوفة القطرية

$D$

يجب أن يتم وضعها بنفس الترتيب. على سبيل المثال، القيمة الذاتية الأولى للمصفوفة القطرية

$D$

يجب أن يكون هو الذي يتوافق مع المتجه الذاتي للعمود الأول من المصفوفة

$P$

فيما يلي العديد من تمارين تخطيط المصفوفة خطوة بخطوة والتي يمكنك التدرب عليها.

حل تمارين المصفوفة القطرية

التمرين 1

قم بتخطيط المصفوفة المربعة التالية ذات البعد 2×2:

$\displaystyle A= \begin{pmatrix}2&2\\[1.1ex] 1&3\end{pmatrix}$

انظر الحل

يجب علينا أولاً تحديد القيم الذاتية للمصفوفة A. لذلك نحسب المعادلة المميزة عن طريق حل المحدد التالي:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2- \lambda &2\\[1.1ex] 1&3-\lambda \end{vmatrix} = \lambda^2-5\lambda +4$

الآن دعونا نحسب جذور كثيرة الحدود المميزة:

$\displaystyle \lambda^2-5\lambda +4=0 \ \longrightarrow \ \begin{cases} \lambda = 4 \\[2ex] \lambda = 1 \end{cases}$

بمجرد الحصول على القيم الذاتية، نقوم بحساب المتجهات الذاتية المرتبطة بكل منها. أولاً، المتجه الذاتي المقابل للقيمة الذاتية 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&2\\[1.1ex] 1&2\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] x+2y = 0\end{array}\right\} \longrightarrow \ x=-2y$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] 1 \end{pmatrix}$

ثم نحسب المتجه الذاتي المرتبط بالقيمة الذاتية 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&2\\[1.1ex] 1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2y = 0 \\[2ex] x-y = 0\end{array}\right\} \longrightarrow \ y=x$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 1 \end{pmatrix}$

نحن نبني المصفوفة

$P$

، التي شكلتها المتجهات الذاتية للمصفوفة:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix}$

وبما أن جميع القيم الذاتية مختلفة، فإن المصفوفة A قابلة للقطر. وبالتالي فإن المصفوفة القطرية المقابلة هي تلك التي لها قيم ذاتية على القطر الرئيسي:

$\displaystyle D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

تذكر أنه يجب وضع القيم الذاتية بنفس ترتيب وضع المتجهات الذاتية في المصفوفة

$P$

في الختام، فإن مصفوفة التغيير الأساسية والمصفوفة القطرية هي:

$\displaystyle P = \begin{pmatrix}-2&1 \\[1.1ex] 1&1 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&4\end{pmatrix}$

تمرين 2

قم بتخطيط المصفوفة المربعة التالية من الرتبة 2:

$\displaystyle A= \begin{pmatrix}3&4\\[1.1ex] -1&-2\end{pmatrix}$

انظر الحل

يجب علينا أولاً تحديد القيم الذاتية للمصفوفة A. لذلك نحسب المعادلة المميزة عن طريق حل المحدد التالي:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3- \lambda &4\\[1.1ex] -1&-2-\lambda \end{vmatrix} = \lambda^2-\lambda -2$

الآن دعونا نحسب جذور كثيرة الحدود المميزة:

$\displaystyle \lambda^2-\lambda -2=0 \ \longrightarrow \ \begin{cases} \lambda = -1 \\[2ex] \lambda = 2 \end{cases}$

بمجرد الحصول على القيم الذاتية، نقوم بحساب المتجهات الذاتية المرتبطة بكل منها. أولاً، المتجه الذاتي المقابل للقيمة الذاتية -1:

$\displaystyle (A+I)v=0$

$\displaystyle \begin{pmatrix}4&4\\[1.1ex] -1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 4x+4y = 0 \\[2ex] -x-y = 0\end{array}\right\} \longrightarrow \ x=-y$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 1 \end{pmatrix}$

ثم نحسب المتجه الذاتي المرتبط بالقيمة الذاتية 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}1&4\\[1.1ex] -1&-4\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \end{pmatrix} =}\begin{pmatrix}0 \\[1.1ex] 0 \end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+4y = 0 \\[2ex] -x-4y = 0\end{array}\right\} \longrightarrow \ x=-4y$

$\displaystyle v = \begin{pmatrix}-4 \\[1.1ex] 1 \end{pmatrix}$

نحن نبني المصفوفة

$P$

، التي شكلتها المتجهات الذاتية للمصفوفة:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1 \end{pmatrix}$

نظرًا لأن جميع القيم الذاتية مختلفة عن بعضها البعض، فإن المصفوفة A قابلة للقياس قطريًا. وبالتالي فإن المصفوفة القطرية المقابلة هي التي تحتوي على القيم الذاتية على القطر الرئيسي:

$\displaystyle D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

تذكر أنه يجب وضع القيم الذاتية بنفس ترتيب وضع المتجهات الذاتية في المصفوفة

$P$

في الختام، فإن مصفوفة التغيير الأساسية والمصفوفة القطرية هي:

$\displaystyle P = \begin{pmatrix}-1&-4 \\[1.1ex] 1&1\end{pmatrix} \qquad D= \begin{pmatrix}-1&0\\[1.1ex] 0&2\end{pmatrix}$

التمرين 3

قم بتخطيط المصفوفة المربعة التالية ذات البعد 3×3:

$\displaystyle A= \begin{pmatrix}2&0&2\\[1.1ex] -1&2&1\\[1.1ex] 0&1&4\end{pmatrix}$

انظر الحل

تتكون الخطوة الأولى من إيجاد القيم الذاتية للمصفوفة A. لذلك نقوم بحساب المعادلة المميزة عن طريق حل محدد المصفوفة التالية:

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&0&2\\[1.1ex] -1&2-\lambda&1\\[1.1ex] 0&1&4-\lambda \end{vmatrix} = -\lambda^3+8\lambda^2-19\lambda+12$

يجب علينا الآن حساب جذور كثيرة الحدود المميزة. وبما أنها متعددة الحدود من الدرجة الثالثة، فإننا نطبق قاعدة روفيني:

$\displaystyle \begin{array}{r|rrrr} & -1&8&-19& 12 \\[2ex] 1 & & -1&7&-12 \\ \hline &-1\vphantom{\Bigl)}&7&-12&0 \end{array}$

وبعد ذلك نجد جذور كثيرة الحدود التي تم الحصول عليها:

$\displaystyle -\lambda^2+7\lambda -12=0 \ \longrightarrow \ \begin{cases} \lambda = 3 \\[2ex] \lambda = 4 \end{cases}$

وبالتالي فإن القيم الذاتية للمصفوفة هي:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 4$

بمجرد العثور على القيم الذاتية، نقوم بحساب المتجهات الذاتية المرتبطة بكل منها. أولاً، المتجه الذاتي المقابل للقيمة الذاتية 1:

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}1&0&2\\[1.1ex] -1&1&1\\[1.1ex] 0&1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2z = 0 \\[2ex] -x+y+z = 0\\[2ex] y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=-2z \\[2ex] y = -3z \end{array}$

$\displaystyle v = \begin{pmatrix}-2 \\[1.1ex] -3 \\[1.1ex] 1\end{pmatrix}$

ثم نحسب المتجه الذاتي المرتبط بالقيمة الذاتية 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}-1&0&2\\[1.1ex] -1&-1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -x+2z = 0 \\[2ex] -x-y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=2z \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}2 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

وأخيرًا، نحسب المتجه الذاتي المرتبط بالقيمة الذاتية 4:

$\displaystyle (A-4I)v=0$

$\displaystyle \begin{pmatrix}-2&0&2\\[1.1ex] -1&-2&1\\[1.1ex] 0&1&0\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -2x+2z = 0 \\[2ex] -x-2y+z = 0\\[2ex] y = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=z \\[2ex] y = 0 \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 1\end{pmatrix}$

نحن نبني المصفوفة

$P$

، التي شكلتها المتجهات الذاتية للمصفوفة:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1 \end{pmatrix}$

نظرًا لأن جميع القيم الذاتية مختلفة عن بعضها البعض، فإن المصفوفة A قابلة للقياس قطريًا. وبالتالي فإن المصفوفة القطرية المقابلة هي تلك التي لها قيم ذاتية على القطر الرئيسي:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

تذكر أنه يجب وضع القيم الذاتية بنفس ترتيب وضع المتجهات الذاتية في المصفوفة

$P$

باختصار، مصفوفة التغيير الأساسي والمصفوفة القطرية هما:

$\displaystyle P = \begin{pmatrix}-2&2&1 \\[1.1ex] -3&-1&0 \\[1.1ex] 1&1&1\end{pmatrix} \qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&4\end{pmatrix}$

التمرين 4

قم بتخطيط المصفوفة المربعة التالية من الترتيب 3، إن أمكن:

$\displaystyle A= \begin{pmatrix}-1&3&1\\[1.1ex] 0&2&0\\[1.1ex] 3&-1&1\end{pmatrix}$

انظر الحل

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}-1-\lambda&3&1\\[1.1ex] 0&2-\lambda&0\\[1.1ex] 3&-1&1-\lambda \end{vmatrix} = -\lambda^3+2\lambda^2+4\lambda-8$

يجب علينا الآن حساب جذور الحد الأدنى متعدد الحدود. نظرًا لأنها متعددة الحدود من الدرجة الثالثة، فإننا نطبق قاعدة روفيني لتحليلها:

$\displaystyle \begin{array}{r|rrrr} & -1&2&\phantom{-}4& -8 \\[2ex] 2 & & -2&0&8 \\ \hline &-1\vphantom{\Bigl)}&0&4&0 \end{array}$

وبعد ذلك نجد جذور كثيرة الحدود التي تم الحصول عليها:

$\displaystyle -\lambda^2+4=0 \ \longrightarrow \ \begin{cases} \lambda = +2 \\[2ex] \lambda = -2 \end{cases}$

وبالتالي فإن القيم الذاتية للمصفوفة هي:

$\lambda=2 \qquad \lambda =2 \qquad \lambda = -2$

القيمة الذاتية لـ -2 هي ذات تعدد جبري بسيط، من ناحية أخرى، القيمة الذاتية لـ 2 هي ذات تعدد مزدوج.

بمجرد العثور على القيم الذاتية، نقوم بحساب المتجهات الذاتية المرتبطة بكل منها. أولاً، المتجه الذاتي المقابل للقيمة الذاتية -2:

$\displaystyle (A+2I)v=0$

$\displaystyle \begin{pmatrix}1&3&1\\[1.1ex] 0&4&0\\[1.1ex] 3&-1&3\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+3y+z = 0 \\[2ex] 4y = 0\\[2ex] 3x-y+3z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] x = -z \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] -1\end{pmatrix}$

دعونا الآن نحسب المتجهات الذاتية المرتبطة بالقيم الذاتية 2.

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix}-3&3&1\\[1.1ex] 0&0&0\\[1.1ex] 3&-1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3x+3y+z = 0 \\[2ex] 0= 0\\[2ex] 3x-y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=0 \\[2ex] z=3x \end{array}$

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 3\end{pmatrix}$

بما أن القيمة الذاتية 2 تتكرر مرتين، نحتاج إلى حساب متجه ذاتي آخر يفي بمعادلات الفضاء الجزئي (أو الفضاء الذاتي):

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] -3\end{pmatrix}$

نحن نبني المصفوفة

$P$

، مكونة من المتجهات الذاتية الثلاثة للمصفوفة:

$\displaystyle P = \begin{pmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{pmatrix}$

ومع ذلك، فإن المتجهات الثلاثة ليست مستقلة خطيًا، لأنه من الواضح أن المتجهات الذاتية ذات القيمة الذاتية 2 عبارة عن مزيج خطي من بعضها البعض. ويمكن إثبات ذلك أيضًا كمحدد للمصفوفة

$P$

يساوي 0 (يحتوي على سطر مليء بالأصفار):

$\displaystyle \text{det}(P) = \begin{vmatrix}1&1&-1 \\[1.1ex] 0&0&0 \\[1.1ex] -1&3&-3 \end{vmatrix}=0$

لذلك، نظرًا لأن المتجهات الذاتية تعتمد خطيًا، فإن المصفوفة A غير قابلة للقياس قطريًا .

التمرين 5

إذا أمكن، قم بتخطيط المصفوفة المربعة التالية ذات الحجم 3×3:

$\displaystyle A= \begin{pmatrix}3&0&0\\[1.1ex] 0&2&1\\[1.1ex] 0&1&2\end{pmatrix}$

انظر الحل

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}$

بما أن السطر الأول يتكون بالكامل من أصفار باستثناء 3، فسوف نستفيد من ذلك لحل محدد المصفوفة بواسطة العوامل المساعدة (أو العوامل المجاورة):

$\displaystyle \begin{aligned} \begin{vmatrix}3-\lambda&0&0\\[1.1ex] 0&2-\lambda&1\\[1.1ex] 0&1&2-\lambda \end{vmatrix}& = (3-\lambda)\cdot \begin{vmatrix} 2-\lambda&1\\[1.1ex]1&2-\lambda \end{vmatrix} \\[3ex] & = (3-\lambda)[\lambda^2 -4\lambda +3] \end{aligned}$

نحن الآن بحاجة إلى حساب جذور كثيرة الحدود المميزة. من الأفضل عدم ضرب الأقواس لأنك ستحصل بعد ذلك على متعددة الحدود من الدرجة الثالثة. من ناحية أخرى، إذا تم حل العاملين بشكل منفصل، فمن الأسهل الحصول على القيم الذاتية:

$\displaystyle (3-\lambda)[\lambda^2 -4\lambda +3]=0 \ \longrightarrow \ \begin{cases} 3-\lambda=0 \ \longrightarrow \ \lambda = 3 \\[2ex] \lambda^2 -4\lambda +3=0 \ \longrightarrow \begin{cases}\lambda = 1 \\[2ex] \lambda = 3 \end{cases} \end{cases}$

وبالتالي فإن القيم الذاتية للمصفوفة هي:

$\lambda=1 \qquad \lambda =3 \qquad \lambda = 3$

$\displaystyle (A-I)v=0$

$\displaystyle \begin{pmatrix}2&0&0\\[1.1ex] 0&1&1\\[1.1ex] 0&1&1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2x = 0 \\[2ex] y+z = 0\\[2ex] y+z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}x=0 \\[2ex] y = -z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] -1 \\[1.1ex] 1\end{pmatrix}$

ثم نحسب المتجهات الذاتية المرتبطة بالقيم الذاتية 3:

$\displaystyle (A-3I)v=0$

$\displaystyle \begin{pmatrix}0&0&0\\[1.1ex] 0&-1&1\\[1.1ex] 0&1&-1\end{pmatrix}\begin{pmatrix}x \\[1.1ex] y \\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 0 = 0 \\[2ex] -y+z = 0\\[2ex] y-z = 0\end{array}\right\} \longrightarrow \ \begin{array}{l}y=z \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 1 \\[1.1ex] 1\end{pmatrix}$

بما أن القيمة الذاتية 3 تتكرر مرتين، نحتاج إلى حساب متجه ذاتي آخر يحقق معادلات الفضاء الذاتي:

$\displaystyle v = \begin{pmatrix}1 \\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

نحن نبني المصفوفة

$P$

، التي شكلتها المتجهات الذاتية للمصفوفة:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}$

على عكس التمرين 4، في هذه الحالة تمكنا من تكوين 3 متجهات مستقلة خطيًا على الرغم من أن التعددية الجبرية للقيمة الذاتية 3 مزدوجة. ويمكن التحقق من ذلك من خلال رؤية محدد المصفوفة

$P$

يعطي نتيجة مختلفة عن 0:

$\displaystyle \text{det}(P) = \begin{vmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{vmatrix} =-2 \neq 0$

يمكننا بالتالي إجراء التحلل القطري للمصفوفة A. والمصفوفة القطرية المقابلة هي التي لها قيم ذاتية على القطر الرئيسي:

$\displaystyle D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

تذكر أنه يجب وضع القيم الذاتية بنفس ترتيب وضع المتجهات الذاتية في المصفوفة

$P$

باختصار، مصفوفة التغيير الأساسية المطلوبة لقطر المصفوفة وشكلها القطري هي:

$\displaystyle P = \begin{pmatrix}0&0&1 \\[1.1ex] -1&1&0 \\[1.1ex] 1&1&0 \end{pmatrix}\qquad D= \begin{pmatrix}1&0&0\\[1.1ex] 0&3&0 \\[1.1ex] 0&0&3\end{pmatrix}$

التمرين 6

قم بإجراء القطر، إن أمكن، للمصفوفة التالية ذات البعد 4×4:

$\displaystyle A=\begin{pmatrix}2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

انظر الحل

$\displaystyle \text{det}(A-\lambda I)= \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}$

وفي هذه الحالة يكون العمود الأخير من المحدد مكونًا من أصفار فقط باستثناء عنصر واحد، ولذلك سنستفيد من ذلك لحساب المحدد بالعوامل المساعدة من خلال هذا العمود:

$\displaystyle \begin{aligned} \begin{vmatrix}2-\lambda&1&2&0\\[1.1ex] 1&-3-\lambda&1&0\\[1.1ex] 0&-1&-\lambda&0\\[1.1ex] 0&0&0&5-\lambda\end{vmatrix}& = (5-\lambda)\cdot \begin{vmatrix}2-\lambda&1&2\\[1.1ex] 1&-3-\lambda&1\\[1.1ex] 0&-1&-\lambda\end{vmatrix}\\[3ex] & = (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda] \end{aligned}$

يجب علينا الآن حساب جذور كثيرة الحدود المميزة. من الأفضل عدم استخدام حاصل ضرب الأقواس لأنك ستحصل بعد ذلك على كثيرة الحدود من الدرجة الرابعة. ومع ذلك، إذا تم حل العاملين بشكل منفصل، فمن الأسهل حساب القيم الذاتية:

$\displaystyle (5-\lambda)[-\lambda^3 -\lambda^2 +6\lambda]=0 \ \longrightarrow \ \begin{cases} 5-\lambda=0 \ \longrightarrow \ \lambda = 5 \\[2ex] -\lambda^3 -\lambda^2 +6\lambda =0 \ \longrightarrow \ \lambda(-\lambda^2 -\lambda +6) =0 \end{cases}$

$\displaystyle \lambda(-\lambda^2 -\lambda +6)=0 \ \longrightarrow \ \begin{cases} \lambda=0 \\[2ex] -\lambda^2 -\lambda +6=0 \ \longrightarrow \ \begin{cases} \lambda=2 \\[2ex] \lambda = -3 \end{cases}\end{cases}$

وبالتالي فإن القيم الذاتية للمصفوفة هي:

$\lambda=0 \qquad \lambda =-3 \qquad \lambda = 2\qquad \lambda = 5$

بمجرد العثور على جميع القيم الذاتية، ننتقل نحو المتجهات الذاتية. نحسب المتجه الذاتي المرتبط بالقيمة الذاتية 0:

$\displaystyle (A-0I)v=0$

$\displaystyle \begin{pmatrix} 2&1&2&0\\[1.1ex] 1&-3&1&0\\[1.1ex] 0&-1&0&0\\[1.1ex] 0&0&0&5\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 2w+x+2y = 0 \\[2ex] w-3x+y = 0\\[2ex] -x=0 \\[2ex] 5z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=0 \\[2ex] z=0 \\[2ex]w=-y \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 0 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

نحسب المتجه الذاتي المرتبط بالقيمة الذاتية -3:

$\displaystyle (A+3I)v=0$

$\displaystyle \begin{pmatrix} 5&1&2&0\\[1.1ex] 1&0&1&0\\[1.1ex] 0&-1&3&0\\[1.1ex] 0&0&0&8\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} 5w+x+2y = 0 \\[2ex] w+y = 0\\[2ex] -x+3y=0 \\[2ex] 8z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=-y \\[2ex]x=3y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-1 \\[1.1ex] 3 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

نحسب المتجه الذاتي المرتبط بالقيمة الذاتية 2:

$\displaystyle (A-2I)v=0$

$\displaystyle \begin{pmatrix} 0&1&2&0\\[1.1ex] 1&-5&1&0\\[1.1ex] 0&-1&-2&0\\[1.1ex] 0&0&0&3\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} x+2y = 0 \\[2ex] w-5x+y = 0\\[2ex] -x-2y=0 \\[2ex] 3z=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} x=-2y \\[2ex] w=-11y \\[2ex] z=0 \end{array}$

$\displaystyle v = \begin{pmatrix}-11 \\[1.1ex] -2 \\[1.1ex] 1 \\[1.1ex]0 \end{pmatrix}$

نحسب المتجه الذاتي المرتبط بالقيمة الذاتية 5:

$\displaystyle (A-5I)v=0$

$\displaystyle \begin{pmatrix} -3&1&2&0\\[1.1ex] 1&-8&1&0\\[1.1ex] 0&-1&-5&0\\[1.1ex] 0&0&0&0\end{pmatrix}\begin{pmatrix}w \\[1.1ex] x \\[1.1ex] y\\[1.1ex] z \end{pmatrix} =\begin{pmatrix}0 \\[1.1ex] 0\\[1.1ex] 0 \\[1.1ex] 0\end{pmatrix}$

$\displaystyle \left.\begin{array}{l} -3w+x+2y = 0 \\[2ex] w-8x+y = 0\\[2ex] -x-5y=0 \\[2ex] 0=0 \end{array}\right\} \longrightarrow \ \begin{array}{l} w=x=y=0 \end{array}$

$\displaystyle v = \begin{pmatrix}0 \\[1.1ex] 0 \\[1.1ex] 0 \\[1.1ex]1 \end{pmatrix}$

نحن نصنع المصفوفة

$P$

، تتكون من المتجهات الذاتية للمصفوفة:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix}$

$\displaystyle D= \begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

تذكر أنه يجب وضع القيم الذاتية بنفس ترتيب وضع المتجهات الذاتية في المصفوفة

$P$

باختصار، تغييرات المصفوفة الأساسية اللازمة لجعل المصفوفة A والمصفوفة في شكل قطري هي:

$\displaystyle P = \begin{pmatrix}-1&-1&-11&0 \\[1.1ex] 0&3&-2&0 \\[1.1ex] 1&1&1&0 \\[1.1ex]0&0&0&1\end{pmatrix} \qquad D=\begin{pmatrix}0&0&0&0\\[1.1ex] 0&-3&0&0 \\[1.1ex] 0&0&2&0\\[1.1ex] 0&0&0&5\end{pmatrix}$

تطبيقات المصفوفات القابلة للقطر

إذا كنت قد وصلت إلى هذا الحد، فربما تتساءل: ما فائدة المصفوفة القابلة للقطر؟

حسنًا، المصفوفات القابلة للقياس القطرية مفيدة جدًا وتستخدم على نطاق واسع في الرياضيات. والسبب هو أن المصفوفة القطرية مليئة عمليًا بالأصفار، وبالتالي تجعل العمليات الحسابية أسهل بكثير.

ومن الأمثلة الواضحة على ذلك قوى المصفوفات القابلة للقطر، إذ يتم تبسيط نتيجتها بالصيغة التالية:

$\displaystyle A^k=PD^kP^{-1}$

ويمكن إثبات هذه المساواة بسهولة عن طريق الاستقراء. لذلك يكفي رفع المصفوفة

$D$

إلى العارض. وبما أنها مصفوفة قطرية، فإن العملية تقتصر على رفع كل حد من القطر الرئيسي إلى الأس:

$\displaystyle D^k = diag(\lambda_1^k,\lambda_2^k, \ldots , \lambda_n^k)$

مثال على قوة مصفوفة قابلة للقطر

لكي نفهم بشكل أفضل، سوف نقوم بحساب قوة المصفوفة القابلة للقطر كمثال:

$\displaystyle A= \begin{pmatrix}2&0\\[1.1ex] 3&1\end{pmatrix}$

مصفوفة التغيير الأساسية

$P$

، التي شكلتها ناقلاتها الذاتية، والمصفوفة القطرية

$D$

، مؤلفة من قيمها الخاصة، وهي:

$\displaystyle P = \begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix} \qquad D= \begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}$

لذا، على سبيل المثال، المصفوفة A مرفوعة إلى 7 تعادل:

$\displaystyle A^7=PD^7P^{-1}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\left.\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\right.^{-1}$

الآن نقوم بعكس المصفوفة

$P:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&2\end{pmatrix}^7\begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

نحن نحل لقوة المصفوفة

$D:$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3\end{pmatrix}\begin{pmatrix}1^7&0\\[1.1ex] 0&2^7\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

$\displaystyle A^7=\begin{pmatrix}0&1 \\[1.1ex] 1&3 \end{pmatrix}\begin{pmatrix}1&0\\[1.1ex] 0&128\end{pmatrix} \begin{pmatrix}-3&1 \\[1.1ex] 1&0 \end{pmatrix}$

وأخيرًا، نقوم بإجراء عمليات ضرب المصفوفات:

$\displaystyle \bm{A^7=}\begin{pmatrix}\bm{128}&\bm{0}\\[1.1ex] \bm{381}&\bm{1}\end{pmatrix}$

كما رأيت، يعد حساب الأس باستخدام مصفوفة قطرية أكثر ملاءمة من ضرب نفس المصفوفة سبع مرات متتالية. ثم تخيل بقيم أس أكبر بكثير.

خصائص المصفوفات القابلة للقطر

خصائص هذا النوع من المصفوفات هي:

إذا كانت المصفوفة
$A$

غير قطري، أي قوة

$A$

.

يمكن وضع جميع المصفوفات تقريبًا في بيئة معقدة
$\mathbb{C}$

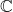
. على الرغم من أن لديك أدناه الاستثناءات التي لا يمكن تحديدها قطريًا.

إذا كانت المصفوفة
$P$

هي مصفوفة متعامدة، ثم نقول أن المصفوفة

$A$

قابلة للقياس بشكل متعامد ، وبالتالي يمكن إعادة كتابة المعادلة:

$\displaystyle A=PDP^t$

تكون المصفوفة قابلة للقطر بواسطة مصفوفة وحدوية إذا كانت مصفوفة عادية وفقط.

بالنظر إلى مصفوفتين قابلتين للقطر، فإنهما تكونان قابلتين للتبديل إذا وفقط إذا كان من الممكن قطرياهما في وقت واحد، أي إذا كانتا تشتركان في نفس الأساس المتعامد الطبيعي للمتجهات الذاتية (أو المتجهات الذاتية).

إذا كان الشكل الداخلي قابلاً للقطر، فإننا نقول إنه قابل للقطر بالتشابه . ومع ذلك، ليست كل الأشكال الداخلية قابلة للقطر، أو بكلمات أخرى، لا يمكن ضمان قطرية الأشكال الداخلية.

القطر المتزامن

يقال إن مجموعة من المصفوفات قابلة للقطر في نفس الوقت إذا كان هناك مصفوفة قابلة للعكس والتي تعمل كأساس لقطر أي مصفوفة في هذه المجموعة. بمعنى آخر، إذا كانت مصفوفتان قطريتين على نفس أساس المتجهات الذاتية، فهذا يعني أنهما قابلتان للقطر في وقت واحد.

بالإضافة إلى ذلك، كما علقنا في خصائص قطري المصفوفة، إذا كانت هناك مصفوفتان قادرتان على القطر في وقت واحد، فيجب عليهما التنقل مع بعضهما البعض.

على سبيل المثال، المصفوفتان التاليتان قابلتان للتبديل، لذا فإنهما تتجهان قطريًا على نفس الأساس للمتجهات الذاتية أو المتجهات الذاتية.

$\displaystyle A=\begin{pmatrix}2&0 \\[1.1ex] 1&-1 \end{pmatrix} \qquad B=\begin{pmatrix}3&0\\[1.1ex] 1&0 \end{pmatrix}$

حتى لو كان لديهم نفس المتجهات الذاتية، فهذا لا يعني أن لديهم نفس القيم الذاتية. في الواقع، على الرغم من أن المصفوفتين A وB أعلاه لهما متجهات ذاتية متشابهة، إلا أن لهما قيمًا ذاتية مختلفة.

مصفوفات غير قابلة للقطر

على الرغم من أن الغالبية العظمى من المصفوفات قابلة للقطر في بيئة الأعداد المركبة، إلا أن بعض المصفوفات لا يمكن قطريًا أبدًا.

تحدث هذه الحقيقة عندما لا يتطابق التعدد الجبري لقيمة ذاتية (أو قيمة ذاتية) مع التعدد الهندسي.

على سبيل المثال، لا يمكن جعل المصفوفة التالية قطرية بأي شكل من الأشكال، فهي “قابلة للتحويل قطريًا”:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] 0&0 \end{pmatrix}$

بالإضافة إلى ذلك، هناك مصفوفات غير قادرة على التخطيط القطري في بيئة الأعداد الحقيقية، ولكنها تقوم بالتخطيط القطري عند التعامل مع الأعداد المركبة، مثل هذه المصفوفة:

$\displaystyle \begin{pmatrix}0&1 \\[1.1ex] -1&0 \end{pmatrix}$

وأخيرًا، هناك بعض إجراءات قطري كتلة المصفوفة التي لا يمكن قطريًا تمامًا، ولكنها أكثر تعقيدًا بعض الشيء. أفضل طريقة معروفة هي التنسيق القطري مع الشكل القانوني الأردني .

قم بتخطيط المصفوفة باستخدام MATLAB

تعتبر برامج الكمبيوتر مفيدة للغاية عندما يتعلق الأمر بتخطيط المصفوفات، خاصة إذا كانت كبيرة جدًا. ومن المؤكد أن البرنامج الأكثر شهرة هو MATLAB ، لذلك سنرى بعد ذلك كيفية تحليل المصفوفة قطريًا باستخدام هذا البرنامج.

التعليمات المستخدمة لتحديد قطري للمصفوفة باستخدام MATLAB هي:

$\displaystyle \text{[P, D] = eig(A)}$

ذهب

$A$

هي المصفوفة التي سيتم قطريها و

$P$

$D$

هي المصفوفات التي يرجعها البرنامج:

$P$

هي المصفوفة التي شكلتها المتجهات الذاتية و

$D$

هي المصفوفة في شكل قطري وشروطها القطرية الرئيسية هي القيم الذاتية.

لذلك، تحتاج فقط إلى إدخال هذا الرمز في البرنامج.

من ناحية أخرى، إذا كنت تريد معرفة القيم الذاتية فقط، فيمكنك استخدام العبارة التالية:

$\displaystyle e= eig(A)}$

ذهب

$e$

هو متجه العمود الذي يُرجعه MATLAB بالقيم الذاتية للمصفوفة

$A$

ما هي المصفوفة القابلة للقطر؟

متى يمكنك جعل المصفوفة قطرية؟

كيفية قطري المصفوفة

حل تمارين المصفوفة القطرية

التمرين 1

تمرين 2

التمرين 3

التمرين 4

التمرين 5

التمرين 6

تطبيقات المصفوفات القابلة للقطر

مثال على قوة مصفوفة قابلة للقطر

خصائص المصفوفات القابلة للقطر

القطر المتزامن

مصفوفات غير قابلة للقطر

قم بتخطيط المصفوفة باستخدام MATLAB

اترك تعليقاً إلغاء الرد